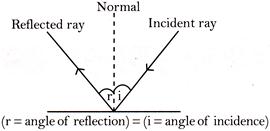
 The ray which falls on the surface of a mirror is called an incident ray. The ray which is sent back after reflection is called reflected ray.
Spherical Mirrors
A spherical mirror is a mirror which has the shape of a piece cut out of a spherical surface. There are two types of spherical mirrors: concave and convex.
The ray which falls on the surface of a mirror is called an incident ray. The ray which is sent back after reflection is called reflected ray.
Spherical Mirrors
A spherical mirror is a mirror which has the shape of a piece cut out of a spherical surface. There are two types of spherical mirrors: concave and convex.
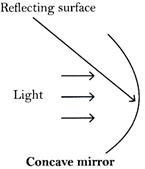
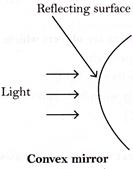 Reflecting surface of a concave mirror bulges inward whereas reflecting surface of a convex mirror bulges outward.
Images
Real Image
The images which are inverted and can be taken on the screen are called real images
Virtual Image
The images which are erect and cannot be taken on the screen are called virtual images.
Reflecting surface of a concave mirror bulges inward whereas reflecting surface of a convex mirror bulges outward.
Images
Real Image
The images which are inverted and can be taken on the screen are called real images
Virtual Image
The images which are erect and cannot be taken on the screen are called virtual images.  Consumers: Animals consume the food prepared by green plants, therefore, animals are called consumers.
Consumers: Animals consume the food prepared by green plants, therefore, animals are called consumers.
 Types of Consumers
Consumers have been classified in the following groups on the basis of their food habits:
Herbivores
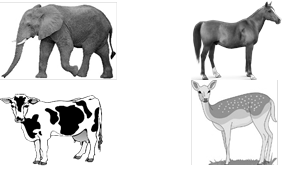
The animals that eat only plants or plant products, are called herbivores. Cow, buffalo, goat, elephant, horse, rabbit, camel, etc. are the examples of herbivores animals.
Types of Consumers
Consumers have been classified in the following groups on the basis of their food habits:
Herbivores
The animals that eat only plants or plant products, are called herbivores. Cow, buffalo, goat, elephant, horse, rabbit, camel, etc. are the examples of herbivores animals.
 Carnivores
The animals that eat only other animals are called carnivores. Tiger, lion, cheetah, wolf, snake, etc. are the examples of omnivores animals.
Carnivores
The animals that eat only other animals are called carnivores. Tiger, lion, cheetah, wolf, snake, etc. are the examples of omnivores animals.
 Omnivores
The animals that eat both plants and animals are called omnivores. Man, bear, dog, crow etc. are the examples of omnivores animals.
Omnivores
The animals that eat both plants and animals are called omnivores. Man, bear, dog, crow etc. are the examples of omnivores animals.
 Scavengers
The animals that eat dead and decaying bodies of other animals are called scavengers. Vulture, hyena, etc. are the examples of scavengers.
Scavengers
The animals that eat dead and decaying bodies of other animals are called scavengers. Vulture, hyena, etc. are the examples of scavengers.
 Decomposers
These are organisms such as bacteria and fungi that break down the dead remains of plants and animals.
Decomposers
These are organisms such as bacteria and fungi that break down the dead remains of plants and animals.
 Parasites
The animals that live in or on the other animals for their survival are called parasites. For example, mosquitoes, flees, leeches, etc.
Parasites
The animals that live in or on the other animals for their survival are called parasites. For example, mosquitoes, flees, leeches, etc.
 Components of Food
The food that we eat is composed of carbohydrates, fats, proteins, vitamins, minerals, water, and roughage.
Functions and Sources of different components of food are given below:
Components of Food
The food that we eat is composed of carbohydrates, fats, proteins, vitamins, minerals, water, and roughage.
Functions and Sources of different components of food are given below:
| Classification | Name of the Nutrient | more...
Fibre to Fabric
Fibre to Fabric
We use clothes for making variety of things like shirts, pants, skirts, sarees, uniforms, bed sheets, blankets, curtains, table cloths, towels, school bags, gunny bags, etc. So clothes are very important for us. In this chapter we will study about different types of fibres.
Clothes: Clothes are fabrics which are made up of yarns and in turn yarns are made up of fibres.
Fibres: Fibres are very thin, thread-like strand from which clothes are made up of.
Yarns: Yarns are made up of fibres. Fibres are turned into long twisted thread by the process of spinning called yarns.
Fabrics: Yarns are woven together to make fabrics. Then fabrics are used to prepare different types of clothes like shirts, pants, bags, etc.
Types of Fibres
There are two types of fibres: natural fibres and synthetic fibres.
Natural Fibres
The fibres which are obtained from natural sources are called natural fibres. Cotton, wool, silk, flax, and jute are the examples of natural fibres.
Cotton
We obtain cotton fibres from cotton plants. Seeds of cotton plants are covered with white, soft cotton fibres. Cotton fibres are separated from seeds by hands or machines.
The preparation of clothes or fabrics from cotton wools or cotton fibres involves mainly three processes which are as follows:
Ginning: The process of separating cotton wool from the cotton seeds is called ginning.
Spinning: The cotton fibres from cotton wool are drawn out and twisted to make yarns. This process is called spinning.
Weaving: In the process of weaving two distinct sets of yarns are interlaced at right angles to form a cloth. Cotton is mainly used to make clothes as it is soft and comfortable to wear. Cotton clothes let air in and can absorb sweat, therefore, very useful specially in and humid weather.
Wool
Wool fibres are obtained from the hair of animals like sheep, goat, rabbit, yak and camel. Wool cut off from the sheep with a thin layer of skin. The process is known as shearing. After shearing the wool is sent to the mills. Where it is cleaned, combed and spun to make fibre is then woven or knitted to make wool clothes. Wool is used for knitting sweaters, shawls and other wool clothes. Wool is a fluffy material and can retain air inside it, therefore, woolen clothes are very useful in winter season.
Silk
Silk fibres are obtained from silk worms. Caterpillars of silkworms cover them self from silk fibres called cocoon. The cocoon is boiled in water to separate the silk fibres from the silkworms. The process is known as reeling. Further the obtained silk fibres twisted to obtains silk yarns then silk yarns are woven to make silk clothes.
The earing of silkworm for the production of silk fibres is called sericulture.
Jute
Jute fibres are obtained from the stem of jute plants. Jute plants more...
Grouping Materials and their Separation
Sorting Materials into Groups
All the objects that we see around us are made up of matter called materials. Like, animals, insects, birds, plants, trees, houses, machines, tools, tables, chairs, clothes, etc. are objects which are made up of matter.
To understand the process of classification, first we have to know the basis of classification.
Basis of Classification
The characteristics or properties, which are taken as the base for the classification of given objects, are called basis of classification. There are a number of characteristics which are taken as the basis for classification. Like 'living and non-living', 'natural and artificial', 'solid, liquid and gas', 'shape', 'colour', etc.
Note: You can also classify the materials by selecting the characteristics as per your own choice.
Properties of Matter
Now let us understand some properties of matter.
Appearance
Some objects have shiny appearance called lustre whereas some materials have dull appearance. For example, gold, silver, copper have shiny appearance whereas paper, wood, rubber have dull appearance.
Hardness and Softness
The materials can be classified on the basis of hardness and softness. Candle, wax, rubber are the examples of soft materials whereas iron, diamond, glass are the examples hard materials.
Solubility
Some materials are soluble in water whereas others are not. Sugar, common salt, washing soda lemon juice are soluble in water whereas glass, plastic, iron, mustard oil, coconut oil are not soluble in water.
Density
Density is the mass per unit volume of a substance. The substances which sink in the water have higher density than water and the substances which float on the water have lower density than water. Substances like iron, copper, aluminium, silver, gold and glass have higher density than water whereas wood, plastic, ice, oil and petrol have lower density than water.
Transparency
All the materials have been classified into three groups on the basis of transparency.
Changes Around Us
Changes Around Us
We observe changes around us all the time. Changes may occur in shape, size, mass, density, colour, position, temperature, structure or in composition of a substance. So we can define a change as:
'Transformation in one or more than one physical or chemical properties of a substance is called change'.
Types of Changes
Types of changes on the basis of either the changes can be reversed to bring back the original substance or not:
Reversible Change
A change which can be reversed to form the 'original substance' is called reversible change. For example, melting of ice, freezing of water, dissolution of salt in water, increase in temperature of a metal rod, etc.
Irreversible Changes
A change which cannot be reversed to form the 'original substance' called irreversible change. For example, burning of wood, ripening of fruit, turning milk sour, etc.
Types of changes on the basis of either a new substance is formed or not:
Physical Change
The change, in which molecules of a substance do not undergo any change or no new substances are formed, are called physical changes. For example, melting of ice, freezing of water, evaporation of water, dissolution of salt in water.
Chemical Change
The change, in which molecules of substance undergo change or new substances are formed, are called chemical changes. For example, burning of paper, rusting of spoliation of food, etc.
Types of changes on the basis of heat absorbed or evolved:
Exothermic
The change in which heat is released. For example, burning of wood.
Endothermic
The change in which heat is absorbed. For example, melting of ice.
Living Organisms and their Habitats
Plants
There are a large number of plants in our surroundings. Plants are living things which can make their own food. They are vital for the survival of animals including us. Let's study about the plants in some detail.
Classification of Plants on the Basis of Bearing Flowers
All the plants has been divided into two groups on the basis that either they bear flower or not.
Flowering Plants: The plants, which bear flowers, are called flowering plants. For example, rose, mango, sunflower, grass, lemon, tulsi, peepal, etc.
Non-Flowering Plants: The plants, which do not bear flowers, are called non-flowering plants. For example, ferns, mosses, algae, fungi, etc.
Classification of Plants on the Basis of Size, Nature of Stem and Life-span
Herbs
Herbs are small plants which have a soft and delicate stem. They have short life-spat. They live for only one or two season. For example, grass, tomato, wheat, paddy, cabbage etc. Banana plant is a herb.
Shrubs
Shrubs are medium sized plants which have hard but not very thick stem. Their lifespan is for many years but less than that of trees. For example, rose, lemon, jasmine, etc.
Trees
Trees are tall and big plants which have hard brown thick stem. Their life-span is for many years. For example, mango, neem, palm, coconut, etc.
Climbers
Climber plants have long, thin and weak stem so they cannot stand upright. They climb up with the help of a support. For example, pea plants, grape vine, glory lily, jasmine, etc.
Creepers
Creeper plants also have long, thin, and weak stem. Creeper plants do not have special organ for climbing up so they spread out on the ground. For example, strawberry, pumpkin, cucumber, etc.
Parts of a Plant
Root stem, leaves, flowers and fruits are the main parts of plants.
Root
This part of a plant grows below the ground. Root fixes the plant firmly to the soil. It absorbs water and minerals from the soil which are essential for the photosynthesis.
Types of Roots
There are mainly two types of roots: tap root and fibrous root.
Tip root: It consists of a main root called tap root from which a number of branching
Roots arise called lateral roots. For example, mango, radish, mustard, etc.
 Fibrous root: It consists of many thin, fibre like roots arising from the base of the stem. For example, grass, wheat, paddy, maize, etc.
Fibrous root: It consists of many thin, fibre like roots arising from the base of the stem. For example, grass, wheat, paddy, maize, etc.
 Functions of Stem:
Functions of Stem:
Body Movements
Body Movements
When we move our body parts like mouth, head, arms, hand and finger, etc. Then our body may remain at the same place. But when we walk by using legs, than we move our whole body from one place to another. The ability of a human being to move its body from one place to another, is called locomotion.
The Skeletal System
The human skeleton or skeletal system is made up of 206 bones. A baby has 300 bones in all But as it grows, some of the bones fuse together or join. Before we learn more about bones and the Joints and where they are joined together, let us take a look at the functions of the skeletal system.
Functions
The bones of our body act as a framework or give a shape to our body. Without bones, our body could be a shapeless mass, say like the body of a snail. It is the movements of the bones that helps us bend, run, walk and so on.
The Skull
Twenty-two bones make up the skull. These are the hardest of all the bones in the body. Some of tee form the cranium, or the cover for the brain. All the bones of the skull except the one forming the lower Jaw are fixed firmly, and cannot move. Only the bone of the lower jaw is capable of movement, which helps us to eat and speak.
 Most of the bones of the skull are fixed. Only the lower jaw can move.
The Spine
The spine also called the vertebral column or backbone, the spine consists of 33 small bones known as vertebrae (singular: vertebra). The vertebrae are hollow at the centre and are joined together form a tube, through which runs the spinal cord.
One of the functions of the vertebral column is to protect the spinal cord. The other functions are to hold the body up and help us bend forward, backward, sideways and twist from the waist.
The Ribcage
Running through the centre of the chest is the breastbone or sternum. Joined to it are 10 pairs of strong, flexible bones called ribs. The ribs curve around and join the chest vertebrae at the back, to form a protective cover for the lungs and heart, called the ribcage. Another two pairs of ribs are joined only to the backbone. These are called floating ribs. The ribs are attached to the sternum in such a way as to allow the ribcage to expand when we inhale, or breathe in and contract when we exhale, or breathe out.
Most of the bones of the skull are fixed. Only the lower jaw can move.
The Spine
The spine also called the vertebral column or backbone, the spine consists of 33 small bones known as vertebrae (singular: vertebra). The vertebrae are hollow at the centre and are joined together form a tube, through which runs the spinal cord.
One of the functions of the vertebral column is to protect the spinal cord. The other functions are to hold the body up and help us bend forward, backward, sideways and twist from the waist.
The Ribcage
Running through the centre of the chest is the breastbone or sternum. Joined to it are 10 pairs of strong, flexible bones called ribs. The ribs curve around and join the chest vertebrae at the back, to form a protective cover for the lungs and heart, called the ribcage. Another two pairs of ribs are joined only to the backbone. These are called floating ribs. The ribs are attached to the sternum in such a way as to allow the ribcage to expand when we inhale, or breathe in and contract when we exhale, or breathe out.
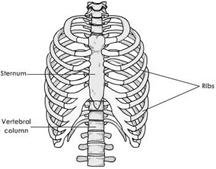 Ribcage
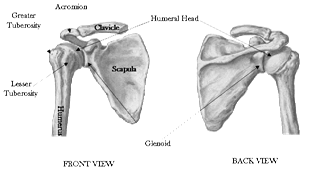
The Shoulder Bones
In shoulder bone each collar bone (clavicle) is attached to a shoulder blade (scapula) and to the breastbone.
Ribcage
The Shoulder Bones
In shoulder bone each collar bone (clavicle) is attached to a shoulder blade (scapula) and to the breastbone.
 more... more... Current Affairs CategoriesArchive
Trending Current Affairs
You need to login to perform this action. |