Closed Circuit: When there is no gap in an electric circuit or the normal path of current has not been interrupted, the circuit is known as closed or complete circuit.
Open Circuit: When there is a gap in an electric circuit or the normal path of current has been interrupted, the circuit is known as an open circuit or incomplete circuit.
Conductors and Insulators
The substances which allow electric current to pass through them are called conductors. For example, copper, gold, silver, aluminium, iron, etc. are good conductors of electricity. The substances which do not allow electric current to pass through them are called insulators For example, wood, plastic, paper, rubber, etc. are insulators.
Electric Cell
An electric cell is a device which can generate electric current in a closed circuit. It is small and easily portable so it is very useful for us. There are a number of machines like watches, calculators, toys, cars, etc. in which electrical cell is used to produce electric current. Dry cell, button cell, solar cell are the examples of electric cell.
Dry Cell
A dry cell is a cylindrical device in which a number of chemicals are stored. It has a metal cap on one side called positive terminal and a metal sheet at other side called negative terminal. It produces electric current from the chemical stored inside it.
Electric Bulb
An electric bulb is a device which produces light energy using electrical energy. It consists of a glass bulb fixed on a metal case, a thin wire fixed between the two thick wires called filament of the bulb and the gas filled inside the glass bulb. When electric current passes through the filament, it emits light which makes the bulb glow.
Magnet
Magnet is a substance which attracts magnetic materials such as iron, nickel, steel and cobalt. Magnets are of different shapes and sizes. For example, U-shaped magnate cylindrical magnet, bar magnet, etc. Each magnet has two poles, southpole and north pole.
Magnetic Materials: The materials which are attracted by a magnet are called magnetic materials. For example, iron, nickel, steel more...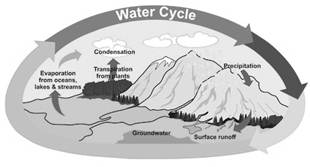 
Water Cycle
Due to sunlight water from the different sources converts into water vapor. These water vapors rise up in the atmosphere and condense to water drops forming cloud. Then they return back to the surface of earth in the form of rain.
Sources of Water
Oceans, seas, lakes, rivers, ponds, rainwater and ground water are the sources of water.
Rain Water: Rainwater is the purest form of water. It collects on the earth in the form of surface water and underground water.
Surface Water: Water present on the surface of the earth in the form of oceans, seas, rivers, lakes, ponds and streams is called surface water. Ocean contains almost 97% of water present on the earth. But it is saline therefore it is unfit for drinking.
Underground Water: Some of the rainwater seeps through the soil and gathers in the non-porous rocks below. This water is known as underground water.
Conservation of Water
As we have studied earlier water is very important for us. So we must conserve water whenever it is possible. Some ways more... 
Problems Based on Coding-decoding
In these types of problems, you will learn to code a word by using a certain pattern or rule.
Problems Based on Puzzle
In these types of problems, the given information is summarized by a table.
| Joseph | John | Ketan | Yash | Arjun |
Compositions
Letters
Letters are mainly of
three types:
Personal Letter: Those
letters which are written to our relatives friends and to known persons. Business
Letter: Those letters which are written to business mass traders and business firms.
Official Letters: Those letters which are written to government officers such
as postmaster, principal, etc.
A letter consists of six
parts which are shown below as example.
1.
Heading
2.
The salutation or greeting
3.
The body
4.
The subscription
5.
Signature
6.
Address
A. You
are Kavi Naik residing at A-39, Mohan Nagar, Allahabad. You with your family
have planned a visit to Delhi to meet your brother, Rahul Naik residing at 31,
Sainik Vihar, Delhi. Write a letter to your brother telling him about the tour.
To,
Rahul Naik
31, Sainik
Vihar, Delhi
20th May,
2018
SUB : TOUR
OF DELHI.
Dear
Rahul,
You will be happy to know
that we are coming to Delhi to spend some time with you. Father, mother, sister
and I, all will reach Delhi by 35th May. Please make sure all the necessary
arrangements are made before we reach. Love from all of us.
Your
brother
Kavi
Naik
B. You
are Ankur Garg studying in R.P.S Public School in DelhL Your family is living in Orissa« Your class
is going to Agra for a picnic. Write a letter to your father requesting him to
grant the permission to go with your class.
To,
Dear
Father,
I am glad to know that you
all are enjoying life there in Orrisa. I have a good news for you that all
students of our class have planned a picnic to Agra. I want to go with them.
The cost of my trip will be paid by the school because I scored highest marks
in the school.
I kindly request you to
please allow me to join this trip.
Yours
lovingly
Ankur Garg
C. You are Suman Kumar studying in class VIth
G.B.S.S. School. Write a letter to the principal of your school requesting him
for school uniform from school stock.
To,
The
Principal
G.B.S.S.
School.
Moti
Nagar, Delhi - 92
26th Aug.
2018
SUB:
SCHOOL UNIFORM
Respected
Sir,
I am Sumant Kumar, a
student of VIth B of your school. My father is a poor man and he is
hardly able to look after the family. Last year I scored more...
Essay
Disaster Management
Management is directly
related to planning about future means, what will be the alternate options if
your present plan does not work. Similarly managing the situation for disaster.
Disasters are generally very destructive in nature. It results huge loss to
life and necessary commodities. If it is a case of flood the basic articles
like food, matches, drinking water, medicines become big issues because these
things get washed away with the flood. Crops, animals and houses also suffer a
big loss. To come to normal situation it takes several years. Earthquake or war
with a country pushes the country a decade behind. Earthquake destroys the
buildings, roads, powder plants and loss to life is large in numbers. People
overcome from financial loss but they can not overcome from emotional loss
occurred in these disasters. So, it is the responsibility of Government to take
action to ensure for the basic facilities in case of disasters. And also it is
the responsibility of a common man to take care of all these things.
Inflation
An indirect attack to
Indian economy- inflation slows down the growth rate of any economy. As
inflation is the flow of money decreases into the market. We know that inflation
is directly proportional to purchasing power of rupees. In the last few months inflation
cracked some new records. It touched around 12% (11.68%) which was really very
high and government was not able to control it. But slowly and gradually it came
down. The inflation is said to be good if it is between 4 to 6%. Inflation
calculation contains so many commodities which are used in day to day life. The
possible factors for the growth of inflation may be American economy, prices of
oil, National Stock Exchange of Europe, production-agriculture and also
political movement in the country. All these mentioned factors decide the
inflation.
Mobile: Need, Fashion
Necessity
The symbol of status is now
the means of communication, a common man is now carrying a mobile phone. Even a
low earning person like vegetable vendor, milk man, bangle seller, street
hawker, newspaper vendor is using mobile. Now-a-days handsets are so cheap that
you can purchase at Rs. 501 a new handset. Wherever you are at any time you can
contact anybody and share your thoughts. For businessman, it is nothing without
mobile. Similarly for a doctor, it can save life of someone who needs a doctor urgently.
Earlier mobile was used by only army and police personnel, but in the last few years,
government decided to make it available for all. So that masses could get
benefit from it. But few handsets which are full of facilities like MP3
ringtone, camera, bluetooth, etc., are symbols of status or way of fashion
also.
Time Machine
Time keeps changing,
everyone know\s this fact but most more...
Paragraphs
A paragraph is a number of
sentences grouped together and relating to one topic, or a group of related
sentences that develop a single point.
A Car Accident
It is the mad craze for
speed that is responsible for many motor accidents. Only last year I witnessed
what might have been a fatal accident on the Kashmir road. I was motoring down
from Srinagar, and as I was nearing Kohala. I came upon the wreckage of two cars
on the road. The smash had been caused, by a car coming down, which swept round
a sharp corner at forty miles an hour and crashed into a car coming up. Happily
no one was killed; but several were badly injured, and the two cars were
wrecked. To drive at such a speed down a twisting mountain road is simply to
court disaster.
Republic Day
India became a Sovereign
Republic on 26th January 1950. On this day our new Constitution prepared by
Constitution Committee was introduced. On this day, the government was formed
by the people of India according to the new Constitution. This day reminds us
of the past and the dark period of the Britishers when we were not free. Many
freedom fighters sacrificed their lives for the freedom of India. The efforts
of the patriots forced the British rulers to quit India for ever. We celebrate
this day in a special manner. The President of India takes the salute of the
Jawans of Army, Navy and Air Fierce. The Government buildings are illuminated
at night.
Diwali Festival
India is called a land of
fairs and festivals. Of all these festivals, Diwali is the most important
religious festival of the Hindus. It is celebrated all over India with great
pomp and show. It generally falls in the end of October or in the beginning of
November. It is celebrated in honour of Rama's return to Ayodhya after fourteen
years of exile. Houses and shops are cleaned and whitewashed for this colourful
festival many days in advance. Sweets, toys and fireworks are in great demand.
Children enjoy themselves heartily They wear new clothes. There is great
feasting. Gifts are exchanged with friends and relatives. At night people
illuminate their houses with earthen lamps, candles or electric bulbs and
fireworks.
Judging Story Logic
In this chapter, we will
learn to make a logical story from the given sentences or incidents in jumbled
form. First two are solved as an example for you.
·
Example
1.
Arrange P, Q, R and S in
order to make a sensible story:
P: He asked her what was
wrong and she replied, ?I wanted to buy a red rose for my mother. But I only
have seventy-five cents, and a rose costs two dollars.? The man smiled and
said, ?Come on in with me. I'll buy you a rose.?
Q: A man stopped at a
flower shop to order some flowers to be wired to his mother who lived two
hundred miles away. As he got out of his car he noticed a young girl sitting on
the curb sobbing.
R: She directed him to a
cemetery, where she placed the rose on a freshly dug grave. The man returned to
the flower shop, canceled the wire order, picked up a bouquet and drove the two
hundred miles to his mother's house.
S: He bought the little
girl her rose and ordered his own mother's flowers. As they were leaving he
offered the girl a ride home. She said, "Yes, please! You can take me to
my mother."
Select the correct option
among the given choices.
(a) PRQS
(b) RPQS
(c) QPSR
(d) SPQR
(e) None
of these
Ans. (c)
2.
Arrange P, Q, R and S in
order to make a sensible story.
P: The two frogs ignored
the comments and tried to jump up out of the pit with all their might. The
other frogs kept telling them to stop, that they were as good as dead.
Q: He jumped even harder and
finally made it out. When he got out, the other frogs said, ?Did you not hear
us?? The frog explained to them that he was deaf. He thought they were
encouraging him the entire time.
R: A group of frogs were
travelling through the woods, and two of them fell into a deep pit. When the
other frogs saw how deep the pit was, they told the two frogs that they were as
good as dead.
S: Finally one of the frogs
took heed to what the other frogs were saying and gave up. He fell down and
died. The other frog continued to jump as hard as he could. Once again, the
crowd of frogs yelled at him to stop the pain and just die.
Select the correct
option among more...
Judging Logic of Action
In this topic, we will learn to arrange sentences, actions
in a logical order.
·
Example 1
Arrange A, B, C and D in logical order to find out the
correct order of actions:
A: Ernest Rutherford was the son of a Scot emigrant in New
Zealand. His parents had 12 children, of whom Ernest was the fourth. His
education was in a state primary school from the age of 15 where children could
get grants of scholarships to secondary schools and to the universities.
B: Rutherford had no intention of following an academic
career. He was not a bookworm. He was good in anything rough-and-tumble and a
keen football player. But he was good at Latin and he had a passion for 'music
and a mechanical bent of mind.
C: At Nelson College, a state boarding school, he was an
outstanding pupil, he sat for a scholarship to Canterbury College and this was
because his masters expected it of him, and he won it.
D: There, Rutherford as a student was fascinated by
Hertz's work on radio weaves and he began to conduct his own experiments in the
clock room of the college, where the students, hung their gowns.
Select the correct answer from the
given options:
(a) ABDC (b) DCAB
(c) ABCD (d)
BACD
(e) None of these
Ans. (c)
·
Example 2
Arrange A, B, C and D in order to logically to find out
the correct order of actions:
A: There are two ways of avoiding fear. One is by
persuading ourselves that we are immune from disaster, and the other is by the
practice of sheer courage. The latter is difficult, and for everybody it
becomes impossible at a certain point.
B: The former has, therefore, always been more popular.
Primitive magic has the purpose of securing safety, either by injuring enemies
or by protecting oneself by talismans, spells or incantations.
C: Without any essential change, belief in such ways of
avoiding danger survived throughout the many centuries of Babylonian
civilisation, spread from Babylon throughout the Empire of Alexander and was
acquired by the Romans in the course of their absorption of Hellenistic
culture.
D: From the Romans it descended to medieval Christendom
and Islam. Science has now lessened the belief in magic, but many people place
more faith in mascots than they are willing to avow, and sorcery, while
condemned by the Church, is still officially a possible sin.
Select the correct answer from the
given options.
(a) ABDC (b) ABCD
(c) ACDB (d) BACD
(e) None of these
Ans. (b)
Judging Completeness of
Process
·
Example 1
Below, you can see a set of
instructions for using a pipette to measure a required amount of water.
Complete the following paragraph which describes how a pipette is used.
1.
Take a pipette and dip the
nozzle into water in a vessel.
2.
Suck out the air through the
other end.
3.
When the water rises to the
mark on the pipette, cover its upper end and take the pipette out.
4.
Then empty the water in the
pipette into a breaker. A pipette is taken and the nozzle is dipped into water.
·
Example 2
Below, you can see a set of
instructions for filling a pen. Complete the following paragraph which
describes how a pen is filled.
1.
Remove the cap and hold the
pen in the left hand.
2.
Dip it into the inkpot.
3.
Catch the ink-filler pin in
the right hand and pull.
4.
Leave it to move back to its
original position.
5.
Bring the pen out and check if
the ink has been filled
Current Affairs CategoriesArchive
Trending Current Affairs
You need to login to perform this action. |
