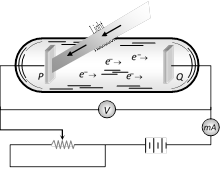
 (2) The battery or other source of potential difference creates an electric field in the direction from anode to cathode.
(3) Light of certain wavelength or frequency falling on the surface of cathode causes a current in the external circuit called photoelectric current.
(4) As potential difference increases, photo electric current also increases till saturation is reached.
(5) When polarity of battery is reversed (i.e. plate Q is at negative potential w.r.t. plate P) electrons start moving back towards the cathode.
(6) At a particular negative potential of plate Q no electron will reach the plate Q and the current will become zero, this negative potential is called stopping potential denoted by \[{{V}_{0}}\]. Maximum kinetic energy of photo electrons in terms of stopping potential will therefore be \[{{K}_{\max }}=(|{{V}_{0}}|)\,eV\]
(2) The battery or other source of potential difference creates an electric field in the direction from anode to cathode.
(3) Light of certain wavelength or frequency falling on the surface of cathode causes a current in the external circuit called photoelectric current.
(4) As potential difference increases, photo electric current also increases till saturation is reached.
(5) When polarity of battery is reversed (i.e. plate Q is at negative potential w.r.t. plate P) electrons start moving back towards the cathode.
(6) At a particular negative potential of plate Q no electron will reach the plate Q and the current will become zero, this negative potential is called stopping potential denoted by \[{{V}_{0}}\]. Maximum kinetic energy of photo electrons in terms of stopping potential will therefore be \[{{K}_{\max }}=(|{{V}_{0}}|)\,eV\] | Element | Work function (eV) | Element | Work function (eV) |
| Platinum | 6.4 | Aluminum | 4.3 |
| Gold | 5.1 | Silver | 4.3 |
| Nickel | 5.1 | Sodium | more...
According to Eienstein's quantum theory light propagates in the bundles (packets or quanta) of energy, each bundle being called a photon and possessing energy.
(1) Energy of photon : Energy of photon is given by
\[E=h\nu =\frac{hc}{\lambda };\] where c = Speed of light, h = Plank's constant \[=6.6\times {{10}^{-34}}\,J-\sec ,\] n = Frequency in Hz, \[\lambda =\]Wavelength of light.
In electron volt \[E(eV)=\frac{hc}{e\lambda }=\frac{12375}{\lambda \,({\AA})}\] \[\approx \frac{12400}{\lambda \,({\AA})}\]
(2) Mass of photon : Actually rest mass of the photon is zero. But it's effective mass is given as
\[E=m{{c}^{2}}=h\nu \]\[\Rightarrow \]\[m=\frac{E}{{{c}^{2}}}=\frac{h\nu }{{{c}^{2}}}=\frac{h}{c\lambda }\].
This mass is also known as kinetic mass of the photon
(3) Momentum of the photon
Momentum \[p=m\times c=\frac{E}{c}=\frac{h\nu }{c}=\frac{h}{\lambda }\]
(4) Number of emitted photons : The number of photons emitted per second from a source of monochromatic radiation of wavelength \[\lambda \] and power P is given as \[(n)=\frac{P}{E}=\frac{P}{h\nu }=\frac{P\lambda }{hc}\]; where E = energy of each photon
(5) Intensity of light (I) : Energy crossing per unit area normally per second is called intensity or energy flux
i.e. \[I=\frac{E}{At}=\frac{P}{A}\] \[\left( \frac{E}{t}=P=\text{radiation}\,\text{power} \right)\]
At a distance r from a point source of power P intensity is given by \[I=\frac{P}{4\pi {{r}^{2}}}\]\[\Rightarrow \]\[I\propto \frac{1}{{{r}^{2}}}\]
(6) Number of photons falling per second (n) : If P is the power of radiation and E is the energy of a photon then \[n=\frac{P}{E}\]
(1) According to Heisenberg's uncertainty principle, it is impossible to measure simultaneously both the position and the momentum of the particle.
(2) Let \[\Delta x\] and \[\Delta p\] be the uncertainty in the simultaneous measurement of the position and momentum of the particle, then \[\Delta x\Delta p=\hbar \]; where \[\hbar =\frac{h}{2\pi }\] and \[h=6.63\times {{10}^{-34}}\,J-s\] is the Planck's constant. \[(\frac{h}{2\pi }=1.05\times {{10}^{-34}}J\text{-}sec\text{)}\]
A more rigorous treatment gives \[\Delta x..\Delta p\ge \frac{\hbar }{2}\,\,\left( \text{or}\,\frac{\text{h}}{\text{4}\pi } \right)\].
(3) If \[\Delta x=0\] then \[\Delta p=\infty \] and if \[\Delta p=0\] then \[\Delta x=\infty \]
i.e., if we are able to measure the exact position of the particle (say an electron) then the uncertainty in the measurement of the linear momentum of the particle is infinite. Similarly, if we are able to measure the exact linear momentum of the particle i.e., \[\Delta p=0\], then we can not measure the exact position of the particle at that time.
 An electron cannot be observed without changing it's momentum
(4) Uncertainty principle successfully explains
(i) Non-existence of electrons in the nucleus
(ii) Finite size of spectral lines.
(5) The Heisenberg uncertainty principle is also applicable to energy and time, angular momentum and angular displacement. Hence \[\Delta E.\,\Delta t\ge \frac{h}{2\pi }\] and \[\Delta L.\,\Delta \theta \ge \frac{h}{2\pi }\]
(6) If the radius of the nucleus is r then the probability of finding the electron inside the nucleus is \[\Delta x=2r\] and uncertainty in momentum is \[\Delta p=\frac{h}{4\pi r}\]
An electron cannot be observed without changing it's momentum
(4) Uncertainty principle successfully explains
(i) Non-existence of electrons in the nucleus
(ii) Finite size of spectral lines.
(5) The Heisenberg uncertainty principle is also applicable to energy and time, angular momentum and angular displacement. Hence \[\Delta E.\,\Delta t\ge \frac{h}{2\pi }\] and \[\Delta L.\,\Delta \theta \ge \frac{h}{2\pi }\]
(6) If the radius of the nucleus is r then the probability of finding the electron inside the nucleus is \[\Delta x=2r\] and uncertainty in momentum is \[\Delta p=\frac{h}{4\pi r}\]
(1) It is used to study the scattering of electron from a solid or to verify the wave nature of electron. A beam of electrons emitted by electron gun is made to fall on nickel crystal cut along cubical axis at a particular angle. Ni crystal behaves like a three dimensional diffraction grating and it diffracts the electron beam obtained from electron gun.
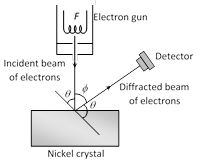 (2) The diffracted beam of electrons is received by the detector which can be positioned at any angle by rotating it about the point of incidence. The energy of the incident beam of electrons can also be varied by changing the applied voltage to the electron gun.
(3) According to classical physics, the intensity of scattered beam of electrons at all scattering angle will be same but Davisson and Germer, found that the intensity of scattered beam of electrons was not the same but different at different angles of scattering. It is maximum for diffracting angle 50° at 54 volt potential difference.
(2) The diffracted beam of electrons is received by the detector which can be positioned at any angle by rotating it about the point of incidence. The energy of the incident beam of electrons can also be varied by changing the applied voltage to the electron gun.
(3) According to classical physics, the intensity of scattered beam of electrons at all scattering angle will be same but Davisson and Germer, found that the intensity of scattered beam of electrons was not the same but different at different angles of scattering. It is maximum for diffracting angle 50° at 54 volt potential difference.
 (4) If the de-Broglie waves exist for electrons then these should be diffracted as X-rays. Using the Bragg's formula \[2d\sin \theta =n\lambda \], we can determine the wavelength of these waves.
where d = distance between diffracting planes, \[\theta =\frac{(180-\varphi )}{2}\]= glancing angle for incident beam = Bragg's angle.
(4) If the de-Broglie waves exist for electrons then these should be diffracted as X-rays. Using the Bragg's formula \[2d\sin \theta =n\lambda \], we can determine the wavelength of these waves.
where d = distance between diffracting planes, \[\theta =\frac{(180-\varphi )}{2}\]= glancing angle for incident beam = Bragg's angle.
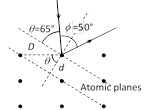 The distance between diffracting planes in Ni-crystal for this experiment is \[d=0.91\,\,\overset{\text{o}}{\mathop{\text{A}}}\,\] and the Bragg's angle \[={{65}^{o}}\]. This gives for \[n=1,\,\,\lambda =2\times 0.91\times {{10}^{-10}}\,\sin {{65}^{o}}=1.65\overset{\text{o}}{\mathop{\text{A}}}\,\]
Now the de-Broglie wavelength can also be determined by using the formula \[\lambda =\frac{12.27}{\sqrt{V}}=\frac{12.27}{\sqrt{54}}=1.67{\AA}\]. Thus the de-Broglie hypothesis is verified.
(5) The Bragg's formula can be rewritten in the form containing interatomic distance D and angle \[\phi \]
\[\because \]\[\theta =90-\frac{\varphi }{2}\,\,\,\text{and }\,d=D\cos \theta =D\sin \frac{\varphi }{2}\]
Using \[\sin \theta =\cos \frac{\varphi }{2}\] \[2d\sin \theta =\lambda \]\[\Rightarrow
\]\[2(D\sin \frac{\varphi }{2}).\cos \frac{\varphi }{2}=\lambda \]\[\Rightarrow \]\[D\,\,\,\sin \,\,\phi =\lambda \]
The distance between diffracting planes in Ni-crystal for this experiment is \[d=0.91\,\,\overset{\text{o}}{\mathop{\text{A}}}\,\] and the Bragg's angle \[={{65}^{o}}\]. This gives for \[n=1,\,\,\lambda =2\times 0.91\times {{10}^{-10}}\,\sin {{65}^{o}}=1.65\overset{\text{o}}{\mathop{\text{A}}}\,\]
Now the de-Broglie wavelength can also be determined by using the formula \[\lambda =\frac{12.27}{\sqrt{V}}=\frac{12.27}{\sqrt{54}}=1.67{\AA}\]. Thus the de-Broglie hypothesis is verified.
(5) The Bragg's formula can be rewritten in the form containing interatomic distance D and angle \[\phi \]
\[\because \]\[\theta =90-\frac{\varphi }{2}\,\,\,\text{and }\,d=D\cos \theta =D\sin \frac{\varphi }{2}\]
Using \[\sin \theta =\cos \frac{\varphi }{2}\] \[2d\sin \theta =\lambda \]\[\Rightarrow
\]\[2(D\sin \frac{\varphi }{2}).\cos \frac{\varphi }{2}=\lambda \]\[\Rightarrow \]\[D\,\,\,\sin \,\,\phi =\lambda \]
(1) Matter wave represents the probability of finding a particle in space.
(2) Matter waves are not electromagnetic in nature.
(3) de-Brogile or matter wave is independent of the charge on the material particle. It means, matter wave of de-Broglie wave is associated with every moving particle (whether charged or uncharged).
(4) Practical observation of matter waves is possible only when the de-Broglie wavelength is of the order of the size of the particles.
(5) Electron microscope works on the basis of de-Broglie waves.
(6) The phase velocity of the matter waves can be greater than the speed of the light.
(7) Matter waves can propagate in vacuum, hence they are not mechanical waves.
(8) The number of de-Broglie waves associated with nth orbital electron is n.
(9) Only those circular orbits around the nucleus are stable whose circumference is integral multiple of de-Broglie wavelength associated with the orbital electron.
According to de-Broglie a moving material particle sometimes acts as a wave and sometimes as a particle.
The wave associated with moving particle is called matter wave or de-Broglie wave and it propagates in the form of wave packets with group velocity.
(1) de-Broglie wavelength : According to de-Broglie theory, the wavelength of de-Broglie wave is given by
\[\lambda =\frac{h}{p}=\frac{h}{mv}=\frac{h}{\sqrt{2mE}}\]\[\Rightarrow \lambda \propto \frac{1}{p}\propto \frac{1}{v}\propto \frac{1}{\sqrt{E}}\]
Where \[h=\] Plank's constant, \[m=\] Mass of the particle, \[\upsilon =\] Speed of the particle, \[E=\] Energy of the particle.
The smallest wavelength whose measurement is possible is that of \[\gamma -\]rays.
The wavelength of matter waves associated with the microscopic particles like electron, proton, neutron, \[\alpha -\]particle etc. is of the order of \[{{10}^{-10}}m\].
(2) de-Broglie wavelength associated with the charged particles : The energy of a charged particle accelerated through potential difference V is \[E=\frac{1}{2}m{{v}^{2}}=qV\]
Hence de-Broglie wavelength \[\lambda =\frac{h}{p}=\frac{h}{\sqrt{2mE}}=\frac{h}{\sqrt{2mqV}}\]
\[{{\lambda }_{Electron}}=\frac{12.27}{\sqrt{V}}\]\[\overset{\text{o}}{\mathop{\text{A}}}\,\],
\[{{\lambda }_{\Pr oton}}=\frac{0.286}{\sqrt{V}}\]\[\overset{\text{o}}{\mathop{\text{A}}}\,\],
\[{{\lambda }_{Deutron}}=\frac{0.202}{\sqrt{V}}\]\[\overset{\text{o}}{\mathop{\text{A}}}\,\],
\[{{\lambda }_{\alpha -particle}}=\frac{0.101}{\sqrt{V}}\]\[\overset{\text{o}}{\mathop{\text{A}}}\,\]
(3) de-Broglie wavelength associated with uncharged particles : For Neutron de-Broglie wavelength is given as
\[{{\lambda }_{Neutron}}=\frac{0.286\times {{10}^{-10}}}{\sqrt{E\,(\text{in}\,eV)}}m=\frac{0.286}{\sqrt{E\,(\text{in}\,eV})}{\AA}\]
Energy of thermal neutrons at ordinary temperature
\[\because \] \[E=kT\Rightarrow \lambda =\frac{h}{\sqrt{2mkT}}\]; where \[T=\] Absolute temperature,
\[k=\] Boltzman's constant \[=1.38\times {{10}^{-23}}\]Joule/kelvin,
So, \[{{\lambda }_{Thermal\ neutron}}=\frac{6.62\times {{10}^{-34}}}{\sqrt{2\times 1.67\times {{10}^{-27}}\times 1.38\times {{10}^{-23}}T}}=\frac{30.83}{\sqrt{T}}{\AA}\]
(4) Ratio of wavelength of photon and electron : The wavelength of a photon of energy E is given by \[{{\lambda }_{ph}}=\frac{hc}{E}\]
While the wavelength of an electron of kinetic energy K is given by \[{{\lambda }_{c}}=\frac{h}{\sqrt{2mK}}\]. Therefore, for the same energy,
the ratio \[\frac{{{\lambda }_{ph}}}{{{\lambda }_{e}}}=\frac{c}{E}\sqrt{2mK}=\sqrt{\frac{2m{{c}^{2}}K}{{{E}^{2}}}}\]
In Bainbridge mass spectrograph, field particles of same velocity are selected by using a velocity selector and then they are subjected to a uniform magnetic field perpendicular to the velocity of the particles. The particles corresponding to different isotopes follow different circular paths as shown in the figure.
(1) Velocity selector : The positive ions having a certain velocity v gets isolated from all other velocity particles. In this chamber the electric and magnetic fields are so balanced that the particle moves undeflected. For this the necessary condition is \[v=\frac{E}{B}\] and E, B and v should be mutually perpendicular to each other.
(2) Analysing chamber : In this chamber magnetic field B is applied perpendicular to the direction of motion of the particle. As a result the particles move along a circular path of radius
\[r=\frac{mE}{qBB'}\Rightarrow \frac{q}{m}=\frac{E}{BB'r}\] also \[\frac{{{r}_{1}}}{{{r}_{2}}}=\frac{{{m}_{1}}}{{{m}_{2}}}\]
In this way the particles of different masses gets deflected on circles of different radii and reach on different points on the photo plate.
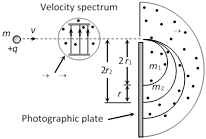 Separation between two traces \[=d=2{{r}_{2}}-2{{r}_{1}}=\frac{2v({{m}_{2}}-{{m}_{1}})}{qB'}\].
Separation between two traces \[=d=2{{r}_{2}}-2{{r}_{1}}=\frac{2v({{m}_{2}}-{{m}_{1}})}{qB'}\].
It is used to measure atomic masses of various isotopes in gas. This is done by measuring q/m of singly ionised positive ion of the gas.
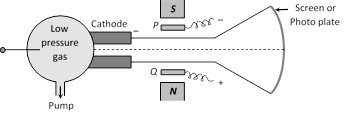 (1) The positive ions are produced in the bulb at the left hand side. These ions are accelerated towards cathode. Some of the positive ions pass through the fine hole in the cathode. This fine ray of positive ions is subjected to electric field E and magnetic field B and then allowed to strike a fluorescent screen (\[\vec{E}||\vec{B}\] but \[\vec{E}\]or \[\vec{B}\ \bot \ \vec{v}\]).
(2) If the initial motion of the ions is in \[+x\] direction and electric and magnetic fields are applied along \[+y\] axis then force due to electric field is in the direction of y-axis and due to magnetic field it is along z-direction.
(1) The positive ions are produced in the bulb at the left hand side. These ions are accelerated towards cathode. Some of the positive ions pass through the fine hole in the cathode. This fine ray of positive ions is subjected to electric field E and magnetic field B and then allowed to strike a fluorescent screen (\[\vec{E}||\vec{B}\] but \[\vec{E}\]or \[\vec{B}\ \bot \ \vec{v}\]).
(2) If the initial motion of the ions is in \[+x\] direction and electric and magnetic fields are applied along \[+y\] axis then force due to electric field is in the direction of y-axis and due to magnetic field it is along z-direction.
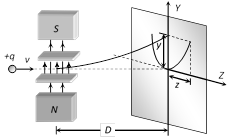 The deflection due to electric field alone \[y=\frac{qELD}{m{{v}^{2}}}\] .....(i)
The deflection due to magnetic field alone \[z=\frac{qBLD}{mv}\] .....(ii)
From equation (i) and (ii), \[{{z}^{2}}=k\left( \frac{q}{m} \right)y\]
where \[k=\frac{{{B}^{2}}LD}{E}\]; This is the equation of parabola. It means all the charged particles moving with different velocities but of same q/m value will strike the screen placed in yz plane on a parabolic track as shown in the above figure.
(3) All the positive ions of same. q/m moving with different velocity lie on the same parabola. Higher is the velocity lower is the value of y and z. The ions of different specific charge will lie on different parabola.
The deflection due to electric field alone \[y=\frac{qELD}{m{{v}^{2}}}\] .....(i)
The deflection due to magnetic field alone \[z=\frac{qBLD}{mv}\] .....(ii)
From equation (i) and (ii), \[{{z}^{2}}=k\left( \frac{q}{m} \right)y\]
where \[k=\frac{{{B}^{2}}LD}{E}\]; This is the equation of parabola. It means all the charged particles moving with different velocities but of same q/m value will strike the screen placed in yz plane on a parabolic track as shown in the above figure.
(3) All the positive ions of same. q/m moving with different velocity lie on the same parabola. Higher is the velocity lower is the value of y and z. The ions of different specific charge will lie on different parabola.
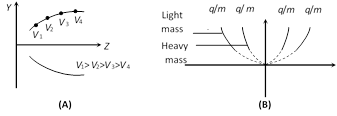 (4) The number of parabola tells the number of isotopes present in the given ionic beam.
(4) The number of parabola tells the number of isotopes present in the given ionic beam.
When potential difference is applied across the electrodes of a discharge tube (\[{{10}^{-3}}\,mm\] of Hg), electrons are emitted from the perforated cathode. As they move towards anode, they gain energy. These energetic electrons when collide with the atoms of the gas in the discharge tube, they ionize the atoms. The positive ions so formed at various places between cathode and anode, travel towards the cathode. Since during their motion, the positive ions when reach the cathode, some pass through the holes in the cathode and a faint luminous glow comes out from each hole on the backside of the cathode. It is called positive rays, which are coming out from the holes.
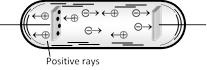 (1) Positive rays are positive ions having same mass if the experimental gas does not have isotopes. However if the gas has isotopes then positive rays are group of positive ions having different masses.
(2) They travel in straight lines and cast shadows of objects placed in their path. But the speed of the positive rays is much smaller than that of cathode rays.
(3) They are deflected by electric and magnetic fields but the deflections are small as compared to that for cathode rays.
(4) They show a spectrum of velocities. Different positive ions move with different velocities. Being heavy, their velocity is much less than that of cathode rays.
(5) q /m ratio of these rays depends on the nature of the gas in the tube (while in case of the cathode rays q/m is constant and doesn't depend on the nature of gas in the tube). q/m for hydrogen is maximum.
(6) They carry energy and momentum. The kinetic energy of positive rays is more than that of cathode rays.
(7) The value of charge on positive rays is an integral multiple of electronic charge. (8) They cause ionisation (which is much more than that produced by cathode rays).
(1) Positive rays are positive ions having same mass if the experimental gas does not have isotopes. However if the gas has isotopes then positive rays are group of positive ions having different masses.
(2) They travel in straight lines and cast shadows of objects placed in their path. But the speed of the positive rays is much smaller than that of cathode rays.
(3) They are deflected by electric and magnetic fields but the deflections are small as compared to that for cathode rays.
(4) They show a spectrum of velocities. Different positive ions move with different velocities. Being heavy, their velocity is much less than that of cathode rays.
(5) q /m ratio of these rays depends on the nature of the gas in the tube (while in case of the cathode rays q/m is constant and doesn't depend on the nature of gas in the tube). q/m for hydrogen is maximum.
(6) They carry energy and momentum. The kinetic energy of positive rays is more than that of cathode rays.
(7) The value of charge on positive rays is an integral multiple of electronic charge. (8) They cause ionisation (which is much more than that produced by cathode rays). Current Affairs CategoriesArchive
Trending Current Affairs
You need to login to perform this action. |