Solved papers for CEE Kerala Engineering CEE Kerala Engineering Solved Paper-2003

done CEE Kerala Engineering Solved Paper-2003 Total Questions - 240

• question_answer1) If the velocity of light c, gravitational constant G and Plancks constant h are chosen as fundamental units, the dimensions of length L in the new system is:
  A)
   \[[{{h}^{1}}{{c}^{1}}{{G}^{-1}}]\]                             
  done clear
  B)
   \[[{{h}^{1/2}}{{c}^{1/2}}{{G}^{-1/2}}]\]
  done clear
  C)
          \[[{{h}^{1}}{{c}^{-3}}{{G}^{1}}]\]             
  done clear
  D)
          \[[{{h}^{1/2}}{{c}^{-3/2}}{{G}^{1/2}}]\]
  done clear
  E)
   
  done clear
  View Answer play_arrow

• question_answer2) A plate has a length\[5\pm 0.1\text{ }cm\]and breadth\[2\pm 0.01\text{ }cm\]. Then the area of the plate is:
  A)
  \[10\pm 0.1\text{ }c{{m}^{2}}\]   
  done clear
  B)
          \[10\pm 0.01\text{ }c{{m}^{2}}\]
  done clear
  C)
         \[10\pm 0.001\text{ }c{{m}^{2}}\]
  done clear
  D)
          \[10\pm 1\text{ }c{{m}^{2}}\]
  done clear
  E)
   \[10c{{m}^{2}}\]
  done clear
  View Answer play_arrow

• question_answer3) A ball hangs from a string inside a train moving along a horizontal straight track. The string is observed to incline towards the rear of the train making a constant small angle with the vertical. It shows that the train is:
  A)
   moving with a uniform acceleration
  done clear
  B)
   moving with a uniform velocity
  done clear
  C)
   moving with a uniform retardation
  done clear
  D)
   moving with an acceleration which is increasing uniformly
  done clear
  E)
   at rest
  done clear
  View Answer play_arrow

• question_answer4) A particle moves along Y-axis in such a way that its y-coordinate varies with time t according to the relation\[y=3+5t+7{{t}^{2}}\]. The initial velocity and acceleration of the particle are respectively:
  A)
   \[14m{{s}^{-1}},\text{ }-5m{{s}^{-2}}\]
  done clear
  B)
   \[19m{{s}^{-1}},-9m{{s}^{-2}}\]
  done clear
  C)
   \[-14m{{s}^{-1}},-5m{{s}^{-2}}\]
  done clear
  D)
   \[3m{{s}^{-1}},-5m{{s}^{-2}}\]
  done clear
  E)
   \[5m{{s}^{-1}},14m{{s}^{-2}}\]
  done clear
  View Answer play_arrow

• question_answer5) An object travels north with a velocity of \[10\text{ }m{{s}^{-1}}\]and then speeds up to a velocity of \[25\text{ }m{{s}^{-1}}\]in 5 s. The acceleration of the object in these 5 s is:
  A)
   \[3\text{ }m{{s}^{-1}}\]in north direction
  done clear
  B)
   \[3\text{ }m{{s}^{-2}}\]in north direction
  done clear
  C)
   \[\text{15 }m{{s}^{-2}}\] in north direction
  done clear
  D)
   \[\text{3 }m{{s}^{-2}}\]in south direction
  done clear
  E)
   \[\text{10 }m{{s}^{-2}}\] in north direction
  done clear
  View Answer play_arrow

• question_answer6) An automobile in travelling at 50 km/h, can be stopped at a distance of 40 m by applying brakes. If the same automobile is travelling at 90 km/h, all other conditions remaining same and assuming no skidding, the minimum stopping distance in metres is:
  A)
   72                         
  done clear
  B)
          92.5                      
  done clear
  C)
   102.6                   
  done clear
  D)
          129.6
  done clear
  E)
   139.6
  done clear
  View Answer play_arrow

• question_answer7) A rifle shoots a bullet with a muzzle velocity of 500 ms1 at a small target 50 m away. To hit the target the rifle must be aimed (take g = 10 \[m{{s}^{-2}}\]):
  A)
   exactly at the target
  done clear
  B)
   10 cm below the target
  done clear
  C)
   10 cm above the target
  done clear
  D)
   5 cm below the target
  done clear
  E)
   5 cm above the target
  done clear
  View Answer play_arrow

• question_answer8) The centripetal acceleration of particle of mass m moving with a velocity v in a circular orbit of radius r is:
  A)
  \[{{v}^{2}}/r\]along the radius, towards the centre
  done clear
  B)
  \[{{v}^{2}}/r\]along the radius, away from the centre
  done clear
  C)
  \[m{{v}^{2}}/r\]along the radius, away from the centre
  done clear
  D)
  \[m{{v}^{2}}/r\]along the radius, towards the centre
  done clear
  E)
  \[vr\]along the radius away from the centre
  done clear
  View Answer play_arrow

• question_answer9) An\[\alpha -\]particle of mass m suffers one dimensional elastic collision with a nucleus of unknown mass. After the collision the\[\alpha -\]particle is scattered directly backwards losing 75% of its kinetic energy. Then the mass of the nucleus is:
  A)
   m                                          
  done clear
  B)
   2m                        
  done clear
  C)
   3m                        
  done clear
  D)
          1m
  done clear
  E)
   5m
  done clear
  View Answer play_arrow

• question_answer10) While driving a car around a curve of 200 m radius, the driver notices that a simple pendulum hung to the roof of the car is making an angle of \[15{}^\circ \]to the horizontal. The speed of the car in km/h is:
  A)
   60.5                                      
  done clear
  B)
   72.5                      
  done clear
  C)
   82.5                      
  done clear
  D)
          92.5
  done clear
  E)
   106.5
  done clear
  View Answer play_arrow

• question_answer11) A stationary body of mass m explodes into three parts having masses in the ratio 1 : 3 : 3. The two fractions with equal masses move at right angles to each other with a velocity of \[1.5\text{ }m{{s}^{-1}}\]Then the velocity of the third body is:
  A)
   \[4.5\sqrt{2}m{{s}^{-1}}\]                          
  done clear
  B)
   \[5\,m{{s}^{-1}}\]          
  done clear
  C)
          \[5\sqrt{32}m{{s}^{-1}}\]     
  done clear
  D)
          \[1.5\,m{{s}^{-1}}\]
  done clear
  E)
   \[1\,m{{s}^{-1}}\]
  done clear
  View Answer play_arrow

• question_answer12) In a simple pendulum the breaking strength of the string is double the weight of the bob. The bob is released from rest when the string is horizontal. The string breaks when it makes an angle 6 with the vertical. Then:
  A)
   \[\theta =30{}^\circ \]                  
  done clear
  B)
   \[\theta =45{}^\circ \]  
  done clear
  C)
          \[\theta =60{}^\circ \]        
  done clear
  D)
          \[\theta ={{\cos }^{-1}}(1/3)\]
  done clear
  E)
   \[\theta ={{\cos }^{-1}}(2/3)\]
  done clear
  View Answer play_arrow

• question_answer13) An object of mass m falls on to a spring of constant k from h. Then the spring undergoes compression by a length\[x\]. The maximum compression x is given by the equation:
  A)
   \[mgh=\frac{1}{2}k{{x}^{2}}\]
  done clear
  B)
   \[mgh(h+x)=\frac{1}{2}k{{x}^{2}}\]
  done clear
  C)
   \[mg(h+x)=-kx\]
  done clear
  D)
   \[mgh=-kx\]
  done clear
  E)
   \[mgh=-\frac{1}{2}k{{x}^{2}}\]
  done clear
  View Answer play_arrow

• question_answer14) A rocket of initial mass 1000 kg ejects mass at a constant rate of 10 kg/s with constant relative speed of\[11\text{ }m{{s}^{-1}}\]. Neglecting gravity, the acceleration of the rocket 1 min after the blast is:
  A)
   \[11/40\,m{{s}^{-2}}\]                 
  done clear
  B)
   \[22/40\,m{{s}^{-2}}\] 
  done clear
  C)
          \[1.1/40\,m{{s}^{-2}}\]
  done clear
  D)
          \[1\,m{{s}^{-2}}\]
  done clear
  E)
   \[11/60\,\,m{{s}^{-2}}\]
  done clear
  View Answer play_arrow

• question_answer15) An elastic ball is dropped from a height h and it rebounds many times from the floor. If the coefficient of restitution is e, the time interval between the second and the third impact, is:
  A)
   \[ev/g\]             
  done clear
  B)
          \[{{e}^{2}}v/g\]              
  done clear
  C)
          \[{{e}^{2}}\sqrt{\left( \frac{8h}{g} \right)}\]      
  done clear
  D)
          \[{{e}^{2}}\sqrt{\left( \frac{h}{g} \right)}\]
  done clear
  E)
   \[{{e}^{2}}\sqrt{\left( \frac{2h}{g} \right)}\]
  done clear
  View Answer play_arrow

• question_answer16) An object of mass m is attached to light string which passess through a hollow tube. The object is set into rotation in a horizontal circle of radius,\[{{r}_{1}}\]. If the string is pulled shortening the radius to\[{{r}_{2}}\], the ratio of new kinetic energy to the original kinetic energy is:
  A)
   \[{{\left( \frac{{{r}_{2}}}{{{r}_{1}}} \right)}^{2}}\]
  done clear
  B)
                          \[{{\left( \frac{{{r}_{1}}}{{{r}_{2}}} \right)}^{2}}\]            
  done clear
  C)
          \[\frac{{{r}_{1}}}{{{r}_{2}}}\]                     
  done clear
  D)
          \[\frac{{{r}_{2}}}{{{r}_{1}}}\]
  done clear
  E)
   1
  done clear
  View Answer play_arrow

• question_answer17) Total angular momentum of a rotating body remains constant, if the net torque acting on the body is:
  A)
   zero         
  done clear
  B)
                         maximum
  done clear
  C)
   minimum      
  done clear
  D)
          unity
  done clear
  E)
   equal to the total angular momentum about a parallel axis
  done clear
  View Answer play_arrow

• question_answer18) A car is racing on a circular track of 180 m radius with a speed of\[32\text{ }m{{s}^{-1}}\]. What should be the banking angle of the road to avoid changes of skidding of the vehicle at this speed without taking into consideration the friction between the tyre and the road?
  A)
   \[45{}^\circ \]                  
  done clear
  B)
          \[60{}^\circ \]                  
  done clear
  C)
   \[30{}^\circ \]                  
  done clear
  D)
          \[15{}^\circ \]
  done clear
  E)
   \[25{}^\circ \]
  done clear
  View Answer play_arrow

• question_answer19) When a ceiling fan is switched on it makes 10 rotations in the first 3s. The number of rotations it makes in the next 3 s, assuming uniform angular acceleration is:
  A)
   40                         
  done clear
  B)
          30                         
  done clear
  C)
   20                         
  done clear
  D)
          10
  done clear
  E)
   50
  done clear
  View Answer play_arrow

• question_answer20) A body is projected vertically upwards from the surface of a planet of radius r with a velocity equal to 1/3rd the escape velocity for that planet. The maximum height attained by the body is:
  A)
   R/2        
  done clear
  B)
                          R/3                       
  done clear
  C)
   R/S                       
  done clear
  D)
          R/8
  done clear
  E)
   R/9
  done clear
  View Answer play_arrow

• question_answer21) A man weighs 80 kg on earth surface. The height above ground where he will weigh 40 kg, is: (radius of earth is 6400 km)
  A)
   0.31 times r
  done clear
  B)
          0.41 times r       
  done clear
  C)
          0.51 times r    
  done clear
  D)
          0.61 times r
  done clear
  E)
   0.82 times r
  done clear
  View Answer play_arrow

• question_answer22) An adulterated sample of milk has a density of \[1032\text{ }kg{{m}^{-3}},\]while pure milk has a density of\[1080\text{ }kg{{m}^{-3}}\]. Then the volume of pure milk in a sample of 10 L of adulterated milk is:
  A)
   0.5 L                     
  done clear
  B)
          1.0 L                     
  done clear
  C)
   2.0 L                     
  done clear
  D)
          3.0 L
  done clear
  E)
   4.0 L
  done clear
  View Answer play_arrow

• question_answer23) Typical silt (hard mud) particle of radius 20 um is on the top of lake water, its density is \[2000\text{ }kg/{{m}^{3}}\]and the viscosity of lake water is 1.0 mPa, density is \[1000\,kg/{{m}^{3}}\]. If the lake is still (has no internal fluid motion). The terminal speed with which the particle hits the bottom of the lake is ... mm/s.
  A)
   0.67                      
  done clear
  B)
          0.77                      
  done clear
  C)
   0.87                      
  done clear
  D)
          0.97
  done clear
  E)
   1.07
  done clear
  View Answer play_arrow

• question_answer24) A solid sphere and a hollow sphere, both of the same size and same mass roll down an inclined plane. Then:
  A)
   solid sphere reaches the ground first
  done clear
  B)
   hollow sphere reaches the ground first
  done clear
  C)
   both spheres reach the ground at the same time
  done clear
  D)
   the time at which the spheres reach the ground cannot be specified by the given data
  done clear
  E)
   the hollow sphere will not roll down
  done clear
  View Answer play_arrow

• question_answer25) If P is the pressure, V the volume, R the gas constant, k the Boltzmann constant and T the absolute temperature, then the number of molecules in the given mass of the gas is given by:
  A)
   \[\frac{PV}{RT}\]                                            
  done clear
  B)
   \[\frac{PV}{kT}\]                            
  done clear
  C)
   \[\frac{PR}{T}\]                               
  done clear
  D)
          \[PV\]
  done clear
  E)
   \[\frac{V}{T}\]
  done clear
  View Answer play_arrow

• question_answer26) An air bubble is released from the bottom of a pond and is found to expand to thrice its original volume as it reached the surface. If the atmospheric pressure is 100 kPa, the absolute pressure at the bottom of lake in kPa is ...(assume no temperature variation):
  A)
   33.3                      
  done clear
  B)
          50.0                      
  done clear
  C)
   100.0                   
  done clear
  D)
          200.0
  done clear
  E)
   300.0
  done clear
  View Answer play_arrow

• question_answer27) During an adiabatic process, the volume of a gas is found to be inversely proportional to the root of its absolute temperature. The ratio \[{{C}_{p}}/{{C}_{V}}\]for the gas is:
  A)
   5/3                       
  done clear
  B)
          4/3                       
  done clear
  C)
          3/2                       
  done clear
  D)
          5/4
  done clear
  E)
   7/4
  done clear
  View Answer play_arrow

• question_answer28) 1 g of steam at\[100{}^\circ C\]and equal mass of ice at \[0{}^\circ C\]are mixed. The temperature of the mixture in steady state will be (latent heat of steam\[=540\text{ }cal/g,\]latent heat of ice = 80 \[cal/g\]):
  A)
   \[50{}^\circ C\]                
  done clear
  B)
          \[100{}^\circ C\]             
  done clear
  C)
          \[67{}^\circ C\]                
  done clear
  D)
          \[33{}^\circ C\]
  done clear
  E)
   \[0{}^\circ C\]
  done clear
  View Answer play_arrow

• question_answer29) The work done by a gas is maximum when it expands:
  A)
   isothermally    
  done clear
  B)
          adiabatically     
  done clear
  C)
          isentropically   
  done clear
  D)
          isobarically
  done clear
  E)
   isochorically
  done clear
  View Answer play_arrow

• question_answer30) A tuning fork of frequency 580 Hz is employed to produce transverse waves on a long rope. The distance between the nearest crusts is found to be 20 cm. The velocity of the wave is:
  A)
   \[58\text{ }m{{s}^{-1}}\]             
  done clear
  B)
          \[580\text{ }m{{s}^{-1}}\]          
  done clear
  C)
          \[20\text{ }m{{s}^{-1}}\]             
  done clear
  D)
          \[\text{29 }m{{s}^{-1}}\]
  done clear
  E)
   \[116\,m{{s}^{-1}}\]
  done clear
  View Answer play_arrow

• question_answer31) A heavy brass sphere is hung from a weightless inelastic spring and as a simple pendulum its time period of oscillation is T. When the sphere is immersed in a non-viscous liquid of density 1/10 that of brass, it will act as a simple pendulum of period:
  A)
   \[T\]                                    
  done clear
  B)
   \[\frac{10}{9}T\]             
  done clear
  C)
          \[\sqrt{\left( \frac{9}{10} \right)}T\]      
  done clear
  D)
          \[\sqrt{\left( \frac{10}{9} \right)}T\]
  done clear
  E)
   \[\frac{9}{100}T\]
  done clear
  View Answer play_arrow

• question_answer32) The distance travelled by a sound wave when a tuning fork completes 25 vib in 16.5 m. If the frequency of the tuning fork is 500 Hz, find the velocity of sound.
  A)
   \[350\text{ }m{{s}^{-1}}\]      
  done clear
  B)
          \[330\text{ }m{{s}^{-1}}\]          
  done clear
  C)
          \[300\text{ }m{{s}^{-1}}\]      
  done clear
  D)
          \[450\text{ }m{{s}^{-1}}\]
  done clear
  E)
   \[500\text{ }m{{s}^{-1}}\]
  done clear
  View Answer play_arrow

• question_answer33) Two instruments having stretched strings are being played in unison. When the tension of one of the instruments is increased by 1%, 3 beats are produced in 2s. The initial frequency of vibration of each wire is:
  A)
   300 Hz                 
  done clear
  B)
          500 Hz 
  done clear
  C)
          1000 Hz               
  done clear
  D)
          400 Hz
  done clear
  E)
   600 Hz
  done clear
  View Answer play_arrow

• question_answer34) Three point charges 1C, 2C and 3C are placed at the corners of an equilateral triangle of side 1m. The work done in bringing these charges to the vertices of a smaller similar triangle of side 0.5 m is:
  A)
   \[2.7\times {{10}^{10}}J\]           
  done clear
  B)
          \[9.9\times {{10}^{10}}J\]           
  done clear
  C)
          \[10.8\times {{10}^{10}}J\]        
  done clear
  D)
          \[5.4\times {{10}^{10}}J\]
  done clear
  E)
   zero
  done clear
  View Answer play_arrow

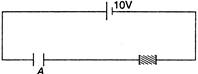
• question_answer35) The capacitors A and B have identical geometry. A material with a dielectric constant 3 is present between the plates of B. The potential difference across A and B are respectively:
  A)
   2.5V, 7.5 V     
  done clear
  B)
                          2V, 8V 
  done clear
  C)
          8V, 2V                 
  done clear
  D)
          7.5V, 2.5V
  done clear
  E)
   3V, 2V
  done clear
  View Answer play_arrow

• question_answer36) An electric bulb is marked 100 W, 230 V. If the supply voltage drops to 115 V, what is the total energy produced by the bulb in 10 min?
  A)
   30 kJ                    
  done clear
  B)
          20 kJ    
  done clear
  C)
   15 kJ                    
  done clear
  D)
   10 kJ
  done clear
  E)
   5kJ
  done clear
  View Answer play_arrow

• question_answer37) A circular coil carrying a current has a radius R. The ratio of magnetic induction at the centre of the coil and at a distance equal to \[\sqrt{3}R\]from the centre of the coil on the axis is:
  A)
   \[1:1\]                 
  done clear
  B)
          \[1:2\]                 
  done clear
  C)
          \[2:1\]                 
  done clear
  D)
          \[1:8\]
  done clear
  E)
   \[8:1\]
  done clear
  View Answer play_arrow

• question_answer38) The examples of diamagnetic, paramagnetic and ferromagnetic materials are respectively:
  A)
   copper, aluminium, iron
  done clear
  B)
   aluminium, copper, iron
  done clear
  C)
   copper, iron, aluminium
  done clear
  D)
   aluminium, iron, copper
  done clear
  E)
   iron, aluminium, copper
  done clear
  View Answer play_arrow

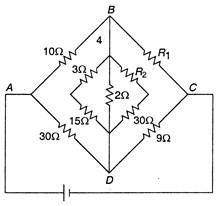
• question_answer39) In the Wheatstones bridge shown below, in order to balance the bridge we must have:
  A)
   \[{{R}_{1}}=3\,\Omega ,{{R}_{2}}=3\,\Omega \]
  done clear
  B)
   \[{{R}_{1}}=6\,\Omega ,{{R}_{2}}=1.5\,\Omega \]
  done clear
  C)
   \[{{R}_{1}}=1.5\,\Omega ,{{R}_{2}}=\]any finite value
  done clear
  D)
   \[{{R}_{1}}=3\,\,\Omega ,{{R}_{2}}=\]any finite value
  done clear
  E)
   \[{{R}_{2}}=1.5\,\,\Omega ,{{R}_{1}}=\]any finite value
  done clear
  View Answer play_arrow

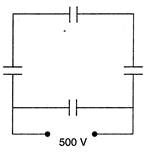
• question_answer40) Four\[10\,\mu F\]capacitors are connected to a 500 V supply as shown in the figure. The equivalent capacitance of the network is:
  A)
   \[40\,\mu F\]                   
  done clear
  B)
          \[20\,\mu F\]   
  done clear
  C)
          \[13.3\,\mu F\]        
  done clear
  D)
          \[10\,\mu F\]
  done clear
  E)
   \[2.5\,\mu F\]
  done clear
  View Answer play_arrow

• question_answer41) A resistor is constructed as hollow cylinder of dimensions\[{{r}_{a}}=0.5\,cm\]and\[{{r}_{b}}=1.0\,cm\]and\[\rho =3.5\times {{10}^{-5}}\Omega m\]. The resistance of the configuration for the length of 5 cm cylinder is ... \[\times {{10}^{-3}}\Omega \].
  A)
   7.42                      
  done clear
  B)
          10.56   
  done clear
  C)
          14.38                   
  done clear
  D)
          16.48
  done clear
  E)
   18.29
  done clear
  View Answer play_arrow

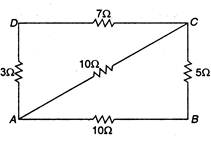
• question_answer42) The resistances are connected as shown in the figure below. Find the equivalent resistance between the points A and B.
  A)
   \[205\,\Omega \]          
  done clear
  B)
          \[10\,\Omega \]             
  done clear
  C)
          \[3.5\,\Omega \]            
  done clear
  D)
          \[5\,\Omega \]
  done clear
  E)
   \[3\,\Omega \]
  done clear
  View Answer play_arrow

• question_answer43) The figure below shows a 2.0 V potentiometer used for the determination of internal resistance of a 2.5 V cell. The balance point of the cell in the open circuit is 75 cm. When a resistor of\[10\,\Omega \]is used in the external circuit of the cell, the balance point shifts to 65 cm length of potentiometer wire. Then the internal resistance of the cell is:
  A)
   \[2.5\,\,\Omega \]                        
  done clear
  B)
          \[2.0\,\,\Omega \]        
  done clear
  C)
   \[1.54\,\,\Omega \]                      
  done clear
  D)
   \[1.0\,\,\Omega \]
  done clear
  E)
   \[0.5\,\,\Omega \]
  done clear
  View Answer play_arrow

• question_answer44) An electric heater boils 1 kg of water in a time\[{{t}_{1}}\]. Another heater boils the same amount of water in a time\[{{t}_{2}}\]. When the two heaters are connected in parallel, the time required by them together to boil the same amount of water is:
  A)
   \[{{t}_{1}}+{{t}_{2}}\]                   
  done clear
  B)
   \[{{t}_{1}}{{t}_{2}}\]                     
  done clear
  C)
   \[\frac{{{t}_{1}}+{{t}_{2}}}{2}\]
  done clear
  D)
          \[\frac{{{t}_{1}}-{{t}_{2}}}{2}\]
  done clear
  E)
   \[\frac{{{t}_{1}}{{t}_{2}}}{{{t}_{1}}+{{t}_{2}}}\]
  done clear
  View Answer play_arrow

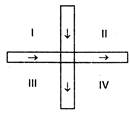
• question_answer45) Two thin metallic strips, carrying current in the direction shown, cross each other perpendicularly without touching but being close to each other, as shown in the figure. The regions which contain some points of zero magnetic induction are:
  A)
   I and II                
  done clear
  B)
          I and III               
  done clear
  C)
          I and IV               
  done clear
  D)
          II and III
  done clear
  E)
   II and IV
  done clear
  View Answer play_arrow

• question_answer46) The force on a conductor of length\[l\]placed in a magnetic field of magnitude B and carrying a current I is given by (\[\theta \]is the angle, the conductor makes with the direction of B):
  A)
   \[F=I\,l\,B\sin \theta \]
  done clear
  B)
          \[F={{I}^{2}}\,l\,{{B}^{2}}\sin \theta \] 
  done clear
  C)
   \[F=I\,l\,B\cos \theta \]
  done clear
  D)
                          \[F=\frac{{{I}^{2}}l}{B}\sin \theta \]
  done clear
  E)
   \[F=\frac{{{I}^{2}}l}{B}\cos \theta \]
  done clear
  View Answer play_arrow

• question_answer47) A needle made of bismuth is suspended freely in a magnetic field. The angle which the needle makes with the magnetic field is:
  A)
   \[0{}^\circ \]                     
  done clear
  B)
          \[45{}^\circ \]
  done clear
  C)
   \[90{}^\circ \]                  
  done clear
  D)
          \[180{}^\circ \]
  done clear
  E)
   any angle with which it is placed
  done clear
  View Answer play_arrow

• question_answer48) The resonant frequency of an LCR circuit occurs at a frequency equal to:
  A)
   \[\frac{1}{LC}\]                               
  done clear
  B)
   \[\frac{1}{\sqrt{LC}}\]  
  done clear
  C)
          \[\frac{1}{LCR}\]             
  done clear
  D)
          \[\frac{1}{CR}\]
  done clear
  E)
   \[\frac{1}{\sqrt{LCR}}\]
  done clear
  View Answer play_arrow

• question_answer49) An AC is given by\[i={{i}_{1}}\cos \omega t+{{i}_{2}}\sin \omega t\]The rms current is given by:
  A)
   \[\frac{{{i}_{1}}+{{i}_{2}}}{\sqrt{2}}\]    
  done clear
  B)
          \[\frac{{{i}_{1}}-{{i}_{2}}}{\sqrt{2}}\]     
  done clear
  C)
          \[\sqrt{\left( \frac{i_{1}^{2}+i_{2}^{2}}{2} \right)}\]       
  done clear
  D)
          \[\sqrt{\left( \frac{i_{1}^{2}-i_{2}^{2}}{2} \right)}\]
  done clear
  E)
   \[\frac{{{i}_{1}}{{i}_{2}}}{\sqrt{2}}\]
  done clear
  View Answer play_arrow

• question_answer50) The coefficient of mutual inductance between the primary and secondary of the coil is 5 H. A current of 10 A is cut off in 0.5 s. The induced emf is:
  A)
   1 V                        
  done clear
  B)
          10 V
  done clear
  C)
   5 V                        
  done clear
  D)
          100 V
  done clear
  E)
   50V
  done clear
  View Answer play_arrow

• question_answer51) If a transformer of an audio amplifier has output impedance\[8000\,\Omega \]and the speaker has input impedance of \[8\Omega \], the primary and secondary turns of this transformer connected between the output of amplifier and to loud speaker should have the ratio:
  A)
   \[1000:1\]                          
  done clear
  B)
   \[100:1\]            
  done clear
  C)
          \[1:32\]              
  done clear
  D)
          \[32:1\]
  done clear
  E)
   \[1:1000\]
  done clear
  View Answer play_arrow

• question_answer52) In the electromagnetic spectrum, the visible spectrum lies between:
  A)
   radio waves and microwaves
  done clear
  B)
   infrared and ultraviolet rays
  done clear
  C)
   microwaves and infrared spectrum
  done clear
  D)
   X-ray and \[\gamma \]-ray spectrum
  done clear
  E)
   ultraviolet and X-ray spectrum
  done clear
  View Answer play_arrow

• question_answer53) Maxwell  in his famous equation of electromagnetism introduced the concept:
  A)
   AC current
  done clear
  B)
   DC current
  done clear
  C)
   displacement current
  done clear
  D)
   impedance
  done clear
  E)
   reactance
  done clear
  View Answer play_arrow

• question_answer54) Out of the following electromagnetic radiations, which has the shortest wavelength?
  A)
   Radio waves    
  done clear
  B)
          Infrared             
  done clear
  C)
          Ultraviolet      
  done clear
  D)
          Visible light
  done clear
  E)
   X-rays
  done clear
  View Answer play_arrow

• question_answer55) In Youngs double slit experiment, the width of one of the slits is slowly increased to make it twice the width of the other slit. Then in the interference pattern:
  A)
   the intensity of maxima increase while that of minima decrease
  done clear
  B)
   the intensities of both maxima and minima decrease
  done clear
  C)
   the intensities of both maxima and minima remain the same
  done clear
  D)
   the intensity of maxima decrease while that of minima increase
  done clear
  E)
   the intensities of both maxima and minima increase
  done clear
  View Answer play_arrow

• question_answer56) Two coherent sources whose intensity ratio is \[81:1\]produce interference fringes. The ratio of minimum   to   maximum   intensity, i.e., \[{{I}_{\min }}:{{I}_{\max }}\]is:
  A)
   \[16:25\]            
  done clear
  B)
          \[9:1\]                 
  done clear
  C)
   \[1:9\]                 
  done clear
  D)
          \[25:16\]
  done clear
  E)
   \[5:4\]
  done clear
  View Answer play_arrow

• question_answer57) An infinitely long rod lies along the axis of concave mirror of focal length\[f\]. The near end of the rod is at a distance\[x>f\]from the mirror. Then the length of the image of the rod is:
  A)
   \[\frac{{{f}^{2}}}{x+f}\]               
  done clear
  B)
          \[\frac{{{f}^{2}}}{x}\]                   
  done clear
  C)
   \[\frac{xf}{x-f}\]             
  done clear
  D)
          \[\frac{xf}{x+f}\]
  done clear
  E)
   \[\frac{{{f}^{2}}}{x-f}\]
  done clear
  View Answer play_arrow

• question_answer58) A beaker containing a liquid appears to be half when it is actually two third full. The refractive index of liquid is:
  A)
   7/6                       
  done clear
  B)
          6/5                       
  done clear
  C)
   3/2                       
  done clear
  D)
          5/4
  done clear
  E)
   4/3
  done clear
  View Answer play_arrow

• question_answer59) If\[{{h}_{1}}\]and\[{{h}_{2}}\]are the heights of the images in conjugate position of a convex lens, then the height of the object is:
  A)
   \[{{h}_{1}}+{{h}_{2}}\] 
  done clear
  B)
          \[{{h}_{1}}-{{h}_{2}}\]  
  done clear
  C)
          \[{{h}_{1}}/{{h}_{2}}\] 
  done clear
  D)
          \[\sqrt{{{h}_{1}}{{h}_{2}}}\]
  done clear
  E)
   \[{{h}_{1}}{{h}_{2}}\]
  done clear
  View Answer play_arrow

• question_answer60) The power of the combination of a convex lens of focal length 50 cm and concave lens of focal length 40 cm is:
  A)
   \[+1\text{ }D\]                
  done clear
  B)
          \[-1\,D\]            
  done clear
  C)
          zero                     
  done clear
  D)
          \[+\,0.5D\]
  done clear
  E)
   \[-\,0.5D\]
  done clear
  View Answer play_arrow

• question_answer61) Image formed by a convex lens is virtual and erect when the object is placed:
  A)
   at F
  done clear
  B)
   between F and the lens
  done clear
  C)
   at 2F
  done clear
  D)
   beyond 2 F
  done clear
  E)
   at infinity
  done clear
  View Answer play_arrow

• question_answer62) The rest mass of photon is:
  A)
   \[\frac{hv}{c}\]               
  done clear
  B)
          \[\frac{hv}{{{c}^{2}}}\]                
  done clear
  C)
          \[\frac{hc}{\lambda }\]                
  done clear
  D)
          zero
  done clear
  E)
   \[\frac{h}{\lambda }\]
  done clear
  View Answer play_arrow

• question_answer63) A charged oil drop of mass \[9.75\times {{10}^{-15}}kg\] and charge\[30\times {{10}^{-16}}C\]is suspended in a uniform electric field existing between two parallel plates. The field between the plates, taking \[(g=10\text{ }m{{s}^{-2}})\]is:
  A)
   3.25 V/m            
  done clear
  B)
          300 V/m             
  done clear
  C)
          325 V/m             
  done clear
  D)
          32.5 V/m
  done clear
  E)
   3000 V/m
  done clear
  View Answer play_arrow

• question_answer64) If the wavelength of incident light changes from 400 nm to 300 nm, the stopping potential for photoelectrons emitted from a surface becomes approximately:
  A)
   1.0V greater   
  done clear
  B)
          1.0V smaller     
  done clear
  C)
          0.5V greater   
  done clear
  D)
          0.5V smaller
  done clear
  E)
   0. IV greater
  done clear
  View Answer play_arrow

• question_answer65) Let the potential energy of hydrogen atom in the ground state be regarded as zero. Then its potential energy in the first excited state will be:
  A)
   20.4 eV               
  done clear
  B)
          13.6 eV               
  done clear
  C)
          3.4 eV                 
  done clear
  D)
          6.8 eV
  done clear
  E)
   10.2 eV
  done clear
  View Answer play_arrow

• question_answer66) Two radioactive nuclides\[x\]and y have half-lives 1 h and 2 h respectively. Initially the samples have equal number of nuclei. After 4 h the ratio of the numbers of\[x\]and y is:
  A)
   \[\frac{1}{2}\]                  
  done clear
  B)
          2
  done clear
  C)
   \[\frac{1}{4}\]
  done clear
  D)
   1
  done clear
  E)
   \[\frac{1}{16}\]
  done clear
  View Answer play_arrow

• question_answer67) \[_{92}{{U}^{238}}\]decays successively to from\[_{90}T{{h}^{234}},\]\[_{91}P{{a}^{234}}{{,}_{92}}{{U}^{234}}{{,}_{90}}T{{h}^{230}}{{,}_{88}}R{{a}^{226}}\]during the reaction the number of\[\alpha -\]particles emitted is:
  A)
   4                            
  done clear
  B)
          3                            
  done clear
  C)
   5                            
  done clear
  D)
          2
  done clear
  E)
   1
  done clear
  View Answer play_arrow

• question_answer68) Let\[{{n}_{e}}\]and\[{{n}_{h}}\]represent the number density of electrons and holes in a semiconductor. Then:
  A)
  \[{{n}_{e}}>{{n}_{h}}\]if the semiconductor is intrinsic
  done clear
  B)
  \[{{n}_{e}}<{{n}_{h}}\]if the semiconductor is intrinsic
  done clear
  C)
  \[{{n}_{e}}\ne {{n}_{h}}\]if the semiconductor is intrinsic
  done clear
  D)
  \[{{n}_{e}}={{n}_{h}}\]if the semiconductor is intrinsic
  done clear
  E)
  \[{{n}_{e}}={{n}_{h}}\]if the semiconductor is extrinsic
  done clear
  View Answer play_arrow

• question_answer69) In a n-p-n transistor amplifier, the collector current is 9 mA. If 90% of the electrons from the emitter reach the collector, then:
  A)
   \[\alpha =0.9,\beta =9.0\]
  done clear
  B)
   the base current is 10 mA
  done clear
  C)
   the emitter current is 1 mA
  done clear
  D)
   \[\alpha =9.0,\text{ }\beta =0.9\]
  done clear
  E)
   \[\alpha =0.99,\text{ }\beta =99.0\]
  done clear
  View Answer play_arrow

• question_answer70) In a properly biased transistor:
  A)
   both depletion layers are equally large
  done clear
  B)
   both depletion layers are equally small
  done clear
  C)
   emitter-base depletion layer is large but base-collector depletion layer is small
  done clear
  D)
   emitter-base depletion layer is small but base-collector depletion layer is large
  done clear
  E)
   both depletion layers vanish
  done clear
  View Answer play_arrow

• question_answer71) A dim star of magnitude\[+14.5\]explodes into a nova of magnitude\[+2\]. The factor by which the brightness of the star has increased is:
  A)
   12.5                      
  done clear
  B)
          \[{{10}^{2}}\]                   
  done clear
  C)
   \[{{10}^{3}}\]                   
  done clear
  D)
          \[{{10}^{4}}\]
  done clear
  E)
   \[{{10}^{5}}\]
  done clear
  View Answer play_arrow

• question_answer72) If the sun becomes twice as hot:
  A)
   the output of radiated energy will be eight times larger
  done clear
  B)
   it will radiate predominantly in the infrared
  done clear
  C)
   it will radiate predominantly in the ultraviolet
  done clear
  D)
   the output of the radiated energy will be eight times smaller
  done clear
  E)
   the frequency spectrum of the radiated energy will not alter
  done clear
  View Answer play_arrow

• question_answer73) The standard adopted for the determination of atomic weight of elements is based on:
  A)
   \[{{H}^{1}}\]                                     
  done clear
  B)
   \[{{C}^{12}}\]
  done clear
  C)
   \[{{O}^{16}}\]                  
  done clear
  D)
          \[{{S}^{32}}\]
  done clear
  E)
   \[C{{l}^{35}}\]
  done clear
  View Answer play_arrow

• question_answer74) Law of multiple proportions is illustrated by one of the following pairs:
  A)
   \[{{H}_{2}}S\]and\[S{{O}_{2}}\]               
  done clear
  B)
   \[N{{H}_{3}}\] and \[N{{O}_{2}}\]
  done clear
  C)
   \[N{{a}_{2}}S\]and\[N{{a}_{2}}O\]
  done clear
  D)
         \[BeO\] and\[BeC{{l}_{2}}\]
  done clear
  E)
   \[{{N}_{2}}O\]and \[NO\]
  done clear
  View Answer play_arrow

• question_answer75) Paramagnetism of oxygen is explained on the basis of its electronic configuration of:
  A)
   \[{{({{\pi }^{*}}2{{p}_{x}})}^{1}}{{(\pi 2{{p}_{y}})}^{1}}\]             
  done clear
  B)
   \[{{({{\pi }^{*}}2{{p}_{y}})}^{1}}{{({{\pi }^{*}}2{{p}_{z}})}^{1}}\]
  done clear
  C)
   \[{{({{\sigma }^{*}}2s)}^{1}}{{(\pi 2{{p}_{y}})}^{1}}\]     
  done clear
  D)
   \[{{({{\sigma }^{*}}2s)}^{1}}{{(\pi 2{{p}_{y}})}^{1}}\]
  done clear
  E)
   \[{{(\pi 2{{p}_{x}})}^{1}}{{(\pi 2{{p}_{y}})}^{1}}\]
  done clear
  View Answer play_arrow

• question_answer76) The van der Waals equation for a real gas is given by the formula\[\left( P+\frac{{{n}^{2}}a}{{{V}^{2}}} \right)\]\[(V-nb)=\]\[nRT,\]where\[P,V,T\]and\[n\]are the pressure, volume, temperature and the number of moles of the gas. Which one is the correct interpretation for the parameter a?
  A)
   The parameter a accounts for the finite size of the molecule, not included temperature in the ideal gas law
  done clear
  B)
   The parameter a accounts for the shape of gas phase molecules
  done clear
  C)
   The   parameter   a   accounts   for intermolecular interactions present in the molecule
  done clear
  D)
   The parameter a has no physical significance and van der Waals introduced it as a numerical correction factor only
  done clear
  E)
   The parameter is a correction factor to the volume of the container
  done clear
  View Answer play_arrow

• question_answer77) Avogadros hypothesis states that:
  A)
   the ideal gas consists of a large number of small particles called molecules
  done clear
  B)
   under the same conditions of temperature and pressure equal volumes of gases contain the same number of molecules
  done clear
  C)
   volume of a definite quantity of gas at constant pressure is directly proportional to absolute temperature
  done clear
  D)
   a given mass of gas at constant pressure is directly   proportional   to   absolute temperature
  done clear
  E)
   for a definite mass of gas at constant temperature the volume is inversely proportional to its pressure
  done clear
  View Answer play_arrow

• question_answer78) The observation that the ground state of nitrogen atom has 3 unpaired electrons in its electronic configuration and not otherwise is associated with:
  A)
   Paulis exclusion principle
  done clear
  B)
   Hunds rule of maximum multiplicity
  done clear
  C)
   Heisenbergs uncertainty relation
  done clear
  D)
   Ritz combination principle
  done clear
  E)
   Valence bond method
  done clear
  View Answer play_arrow

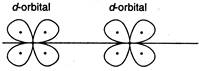
• question_answer79) Which of the following overlaps leads to bonding?
  A)
   
  done clear
  B)
   
  done clear
  C)
   
  done clear
  D)
   
  done clear
  E)
   
  done clear
  View Answer play_arrow

• question_answer80) In the periodic table metallic character of elements shows one of the following trend:
  A)
   decreases down the group and increases across the period
  done clear
  B)
   increases down the group and decreases across the period
  done clear
  C)
   increases across the period and also down the group
  done clear
  D)
   decreases across the period and also down the group
  done clear
  E)
   decreases down the group and remains constant across the period
  done clear
  View Answer play_arrow

• question_answer81) Which of the following statements is correct?
  A)
   All carbon to carbon bonds contain a\[\sigma -\]bond and one or more\[\pi -\]bonds
  done clear
  B)
   All carbon to hydrogen bonds are\[\pi -\]bonds
  done clear
  C)
   All oxygen to hydrogen bonds are hydrogen bonds
  done clear
  D)
   All carbon to hydrogen bonds are \[\sigma -\]bonds
  done clear
  E)
   All carbon to carbon bonds are\[\sigma -\]bonds
  done clear
  View Answer play_arrow

• question_answer82) An example of a polar covalent compound is:
  A)
   \[KCl\]                
  done clear
  B)
         \[NaCl\]
  done clear
  C)
   \[CC{{l}_{4}}\]                 
  done clear
  D)
         \[HCl\]
  done clear
  E)
   \[C{{H}_{4}}\]
  done clear
  View Answer play_arrow

• question_answer83) If\[117g\text{ }NaCl\]is dissolved in 1000 got water the concentration of the solution is said to be:
  A)
   2 molar               
  done clear
  B)
          2 molal
  done clear
  C)
   1 normal            
  done clear
  D)
          1 molal
  done clear
  E)
   2 normal
  done clear
  View Answer play_arrow

• question_answer84) A solution of 4.5 g of a pure non-electrolyte in 100 g of water was found to freeze at\[0.465{}^\circ C\]. The molecular weight of the solute is closest to: \[({{k}_{f}}=1.86)\]
  A)
   135.0                   
  done clear
  B)
          172.0
  done clear
  C)
   90.0                      
  done clear
  D)
          86.2
  done clear
  E)
   180.0
  done clear
  View Answer play_arrow

• question_answer85) The enthalpy of vaporization of substance is \[840\text{ }J\text{ m}o{{l}^{-1}}\]and its boiling point is\[-173{}^\circ C\]. Its entropy of vaporization is:
  A)
   \[42\text{ }J\text{ }mo{{l}^{-1}}{{K}^{-1}}\]
  done clear
  B)
   \[21\text{ }J\text{ }mo{{l}^{-1}}{{K}^{-1}}\]
  done clear
  C)
   \[84\text{ }J\text{ m}o{{l}^{-1}}{{K}^{-1}}\]
  done clear
  D)
   \[8.4\text{ }J\text{ mo}{{l}^{-1}}{{K}^{-1}}\]
  done clear
  E)
   \[0.028\text{ }J\text{ }mo{{l}^{-1}}{{K}^{-1}}\]
  done clear
  View Answer play_arrow

• question_answer86) Given   the   following   thermochemical equations: \[Zn+\frac{1}{2}{{O}_{2}}\xrightarrow[{}]{{}}ZnO+84,000\,cal\] \[Hg+\frac{1}{2}{{O}_{2}}\xrightarrow[{}]{{}}HgO+21,700\,cal\] Accordingly the heat of reaction for the following reaction, \[Zn+HgO\xrightarrow[{}]{{}}Hg+\]heat is:
  A)
   105, 700 cal    
  done clear
  B)
          61, 000 cal
  done clear
  C)
   105, 000 cal    
  done clear
  D)
          60, 000 cal
  done clear
  E)
   62, 300 cal
  done clear
  View Answer play_arrow

• question_answer87) A saturated solution of\[Ca{{F}_{2}}\]is\[2\times {{10}^{-4}}mol/L\] Its solubility product constant is:
  A)
   \[2.6\times {{10}^{-9}}\]     
  done clear
  B)
          \[4\times {{10}^{-8}}\]
  done clear
  C)
   \[8\times {{10}^{-12}}\]              
  done clear
  D)
          \[3.2\times {{10}^{-11}}\]
  done clear
  E)
   \[8\times {{10}^{-10}}\]
  done clear
  View Answer play_arrow

• question_answer88) For the reaction\[{{H}_{2}}(g)+{{I}_{2}}(g)2HI(g),\]the equilibrium constants expressed in terms of concentrations\[{{K}_{c}}\]and in terms of partial pressures\[{{K}_{p}},\]are related as:
  A)
   \[{{K}_{p}}={{K}_{c}}{{(RT)}^{2}}\]
  done clear
  B)
   \[{{K}_{p}}={{K}_{c}}{{(RT)}^{-2}}\]
  done clear
  C)
   \[{{K}_{p}}={{K}_{c}}\]
  done clear
  D)
   \[{{K}_{c}}={{K}_{p}}(RT)\]
  done clear
  E)
   \[{{K}_{c}}={{K}_{p}}{{(RT)}^{-1}}\]
  done clear
  View Answer play_arrow

• question_answer89) Which of the following\[1:1\]mixture will act as buffer solution?
  A)
  \[HCl\]and \[NaOH\]
  done clear
  B)
   \[KOH\] and \[C{{H}_{3}}COOH\]
  done clear
  C)
   \[C{{H}_{3}}COOH\] and \[NaCl\]
  done clear
  D)
   \[C{{H}_{3}}COONa\] and \[N{{H}_{4}}OH\]
  done clear
  E)
   \[C{{H}_{3}}COOH\] and\[C{{H}_{3}}COONa\]
  done clear
  View Answer play_arrow

• question_answer90) What is potential of platinum wire dipped into a solution of\[0.1\,M\,in\,S{{n}^{2+}}\]and\[0.01\,M\,in\,S{{n}^{4+}}\]?
  A)
   \[E{}^\circ \]                     
  done clear
  B)
          \[E{}^\circ +0.059\]
  done clear
  C)
   \[E{}^\circ +\frac{0.059}{2}\]    
  done clear
  D)
          \[E{}^\circ -0.059\]
  done clear
  E)
   \[E{}^\circ -2\times 0.59\]
  done clear
  View Answer play_arrow

• question_answer91) In one of the following reactions\[HN{{O}_{3}}\]does not behave as an oxidizing agent. Identify it:
  A)
   \[{{I}_{2}}+10HN{{O}_{3}}\xrightarrow{{}}2HI{{O}_{3}}+10N{{O}_{2}}\]\[+4{{H}_{2}}O\]
  done clear
  B)
   \[3Cu+8HN{{O}_{3}}\xrightarrow{{}}3Cu{{(N{{O}_{3}})}_{2}}\]\[+2NO+4{{H}_{2}}O\]
  done clear
  C)
   \[4Zn+10HN{{O}_{3}}\xrightarrow[{}]{{}}4Zn{{(N{{O}_{3}})}_{2}}\]\[+N{{H}_{4}}N{{O}_{3}}+3{{H}_{2}}O\]
  done clear
  D)
   \[N{{O}_{3}}+3F{{e}^{2+}}+4{{H}^{+}}\xrightarrow[{}]{{}}NO\]\[+3F{{e}^{3+}}+2{{H}_{2}}O\]
  done clear
  E)
   \[2HN{{O}_{3}}+{{P}_{2}}{{O}_{5}}\xrightarrow{{}}2HP{{O}_{3}}+{{N}_{2}}{{O}_{5}}\]
  done clear
  View Answer play_arrow

• question_answer92) Which of the following statement is not correct?
  A)
   In zero order reaction the rate of the reaction remains constant throughout
  done clear
  B)
   A second order reaction would become a pseudo first order reaction when one of the reactants is taken in large excess
  done clear
  C)
   The value of first order rate constant expends on the units of the concentration terms used
  done clear
  D)
   In a first order reaction the plot of log \[(\alpha -x)vs\]time gives a straight line
  done clear
  E)
   The value of\[{{t}_{1/2}}\]for a first order reaction is independent of initial concentration
  done clear
  View Answer play_arrow

• question_answer93) Radioactive decay series of uranium is denoted as:
  A)
   \[4n+1\]             
  done clear
  B)
          \[4n+2\]
  done clear
  C)
   \[4n\]                  
  done clear
  D)
          \[4n+3\]
  done clear
  E)
   \[4n+4\]
  done clear
  View Answer play_arrow

• question_answer94) The number of isomeric hexanes is:
  A)
   5                            
  done clear
  B)
          2
  done clear
  C)
   3                            
  done clear
  D)
          4
  done clear
  E)
   6
  done clear
  View Answer play_arrow

• question_answer95) The coagulating power of an electrolyte for arsenious sulphide decreases in the order:
  A)
   \[N{{a}^{+}}>A{{l}^{3+}}>B{{a}^{2+}}\]
  done clear
  B)
   \[PO_{4}^{3-}>SO_{4}^{2-}>C{{l}^{-}}\]
  done clear
  C)
   \[Cl>SO_{4}^{2-}>PO_{4}^{3-}\]
  done clear
  D)
  \[A{{l}^{3+}}>B{{a}^{2+}}>N{{a}^{+}}\]
  done clear
  E)
   \[N{{a}^{+}}>B{{a}^{2+}}>PO_{4}^{3-}\]
  done clear
  View Answer play_arrow

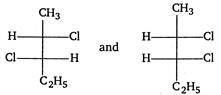
• question_answer96) The two optical isomers given below, namely:
  A)
   enantiomers   
  done clear
  B)
   geometrical isomers
  done clear
  C)
   diastereomers  
  done clear
  D)
   structural isomers
  done clear
  E)
   conformational isomers
  done clear
  View Answer play_arrow

• question_answer97) Which of the following statement is wrong?
  A)
   Using Lassaignes test nitrogen and sulphur present in organic compound can be tested
  done clear
  B)
   Using Beilsteins test the presence of halogen in a compound can be tested
  done clear
  C)
   In Lassaignes filtrate the nitrogen present in a organic compound is converted into\[NaCN\]
  done clear
  D)
   Lassaignes test fail to identify nitrogen in diazo compound
  done clear
  E)
   In the estimation of carbon, an organic compound is heated with\[CaO\]in a combustion tube
  done clear
  View Answer play_arrow

• question_answer98) Cist-trans isomers generally:
  A)
   contain an asymmetric carbon atom
  done clear
  B)
   rotate the plane of polarized light
  done clear
  C)
   are enantiomorphs
  done clear
  D)
   contain a triple bond
  done clear
  E)
   contain double bonded carbon atoms
  done clear
  View Answer play_arrow

• question_answer99) Wurtzs reaction involves the reduction of alkyl halide with:
  A)
  \[Zn/HCl\]       
  done clear
  B)
          \[HI\]
  done clear
  C)
  \[Zn/Cu\]couple  
  done clear
  D)
          Na in ether
  done clear
  E)
  \[Zn\]in an inert solvent
  done clear
  View Answer play_arrow

• question_answer100) The reaction \[{{C}_{12}}{{H}_{26}}\xrightarrow[{}]{{}}{{C}_{6}}{{H}_{12}}+{{C}_{6}}{{H}_{14}}\]represent:
  A)
   substitution    
  done clear
  B)
          synthesis
  done clear
  C)
   cracking              
  done clear
  D)
          polymerization
  done clear
  E)
   addition
  done clear
  View Answer play_arrow

• question_answer101) The compound that does not answer iodoform test is:
  A)
   ethanol              
  done clear
  B)
          ethanol
  done clear
  C)
   methanol      
  done clear
  D)
          propanone
  done clear
  E)
   acetophenone
  done clear
  View Answer play_arrow

• question_answer102) Which one of the following compound reacts with chlorobenzene to produce DDT?
  A)
   Acetaldehyde
  done clear
  B)
   Nitrobenzene
  done clear
  C)
   m-chloroacetaldehyde
  done clear
  D)
   Trichloroacetaldehyde
  done clear
  E)
   Benzene
  done clear
  View Answer play_arrow

• question_answer103) Conversion of benzaldehyde to 3-phenylprop-2-en-l-oic acid is:
  A)
   Perkin condensation
  done clear
  B)
   Claisen condensation
  done clear
  C)
   oxidative addition
  done clear
  D)
   Aldol condensation
  done clear
  E)
   none of the above
  done clear
  View Answer play_arrow

• question_answer104) Which of the following compounds forms an addition compound with\[C{{H}_{3}}MgBr,\]which on hydrolysis produce a secondary alcohol?
  A)
   \[HCHO\]
  done clear
  B)
   \[C{{H}_{3}}CHO\] \[RCHO+Grignard\text{ }reagent\xrightarrow{{}}\] secondary alcohol
  done clear
  C)
   \[C{{H}_{3}}OC{{H}_{3}}\]
  done clear
  D)
   \[C{{H}_{3}}COC{{H}_{3}}\]
  done clear
  E)
   \[C{{H}_{3}}COOC{{H}_{3}}\]
  done clear
  View Answer play_arrow

• question_answer105) Which of the following pairs are correctly matched?

  1. Haber process	Manufacture of ammonia
  2. Leblanc process	Manufacture of sulphuric acid
  3. Birkeland-Eyde process	Manufacture of nitric acid
  4. Solvay process	Manufacture of sodium carbonate

  Select the correct answer using the codes given below:
  A)
   2, 3 and 4           
  done clear
  B)
   1, 2, 3 and 4
  done clear
  C)
   1, 2 and 4      
  done clear
  D)
          1, 2 and 3
  done clear
  E)
   1, 3 and 4
  done clear
  View Answer play_arrow

• question_answer106) Which of the following compounds on treatment first with\[NaN{{O}_{2}}/HCl\]and then coupled     with     phenol     produces p-hydroxyazobenzene?
  A)
   Nitrobenzene  
  done clear
  B)
          Azobenzene
  done clear
  C)
   Phenol                
  done clear
  D)
          Phenyl isocyanide
  done clear
  E)
   Aniline
  done clear
  View Answer play_arrow

• question_answer107) Initial setting of cement is mainly due to:
  A)
   hydration and gel formation
  done clear
  B)
   dehydration and gel formation
  done clear
  C)
   hydration and hydrolysis
  done clear
  D)
   dehydration and dehydrolysis
  done clear
  E)
   hydration and oxidation
  done clear
  View Answer play_arrow

• question_answer108) A certain metal will liberate hydrogen from dilute acids. It will react with water to form hydrogen only when the metal is heated and the water is in the form of steam. The metal is probably:
  A)
   iron                                      
  done clear
  B)
   potassium
  done clear
  C)
   copper                
  done clear
  D)
          mercury
  done clear
  E)
   sodium
  done clear
  View Answer play_arrow

• question_answer109) The number of \[\alpha \] and\[\beta \]particles emitted in the chain of reactions leading to the decay of \[_{92}^{238}U\]to\[_{82}^{206}Pb\]:
  A)
  \[8\beta \]particles and \[6\alpha \] particles
  done clear
  B)
   \[5\alpha \] particles and\[0\beta \]particles
  done clear
  C)
   \[8\alpha \] and\[6\beta \]particles
  done clear
  D)
   \[10\alpha \]particles and\[10\beta \]particles
  done clear
  E)
   \[5\alpha \]particles and\[2\beta \]particles
  done clear
  View Answer play_arrow

• question_answer110) Hydrogen peroxide when added to a solution of potassium permanganate acidified with sulphuric acid:
  A)
   forms water only
  done clear
  B)
   acts as an oxidizing agent
  done clear
  C)
   acts as a reducing agent
  done clear
  D)
   reduces sulphuric acid
  done clear
  E)
   produces hydrogen
  done clear
  View Answer play_arrow

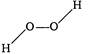
• question_answer111) The equilibrium molecular structure of hydrogen peroxide is:
  A)
   Planar as given below
  done clear
  B)
   linear
  done clear
  C)
   tetrahedral
  done clear
  D)
   non planar
  done clear
  E)
   planar as given below
  done clear
  View Answer play_arrow

• question_answer112) Consider the following compounds: 1. Sulphur dioxide            2. Hydrogen peroxide 3. Ozone Among these compounds identify those that can act as bleaching agent:
  A)
   1 and 3                                
  done clear
  B)
   2 and 3
  done clear
  C)
   1 and 2                
  done clear
  D)
          1, 2 and 3
  done clear
  E)
   1 only
  done clear
  View Answer play_arrow

• question_answer113) Alkali metals have high oxidation potential and hence, they behave as:
  A)
   oxidizing agents
  done clear
  B)
          Lewis bases
  done clear
  C)
   reducing agents
  done clear
  D)
          electrolytes
  done clear
  E)
   Bronsted bases
  done clear
  View Answer play_arrow

• question_answer114) Water is oxidized to oxygen by:
  A)
   \[Cl{{O}_{2}}\]                 
  done clear
  B)
          \[KMn{{O}_{4}}\]
  done clear
  C)
   \[{{H}_{2}}{{O}_{2}}\]                  
  done clear
  D)
          fluorine
  done clear
  E)
   ozone
  done clear
  View Answer play_arrow

• question_answer115) Identify the incorrect statement:
  A)
   The molarity of a solution is independent of temperature
  done clear
  B)
   The tendency for catenation is much higher for carbon than for silicon
  done clear
  C)
   Nitriles and iso nitriles constitute metamers
  done clear
  D)
   t -butyl 1-carbocation has planar carbons and is very reactive
  done clear
  E)
   Zirconium and Hafnium are strikingly similar because of their almost same ionic radii
  done clear
  View Answer play_arrow

• question_answer116) The magnetic momenta, of transition metals is related to the number of unpaired electrons, n as:
  A)
   \[\mu =n{{(n+2)}^{2}}\]
  done clear
  B)
          \[\mu ={{n}^{2}}(n+2)\]
  done clear
  C)
   \[\mu =n/(n+2)\]
  done clear
  D)
          \[\mu =n/\sqrt{(n+2)}\]
  done clear
  E)
   \[\mu =\sqrt{n+(n+2)}\]
  done clear
  View Answer play_arrow

• question_answer117) Which one of the following statement is wrong?
  A)
   The IUPAC name of\[[Co{{(N{{H}_{3}})}_{6}}C{{l}_{3}}]\]is hexamine cobalt (III) chloride
  done clear
  B)
   Dibenzol peroxide is a catalyst in the polymerization of PVC
  done clear
  C)
   Borosilicate glass is heat resistant
  done clear
  D)
   Concentrated\[HN{{O}_{3}}\]can be safely transported in aluminium containers
  done clear
  E)
  \[p{{K}_{a}}\]of trichloroacetic acid is less than that of acetic acid
  done clear
  View Answer play_arrow

• question_answer118) Which of the following is not a thermoplastic?
  A)
   Polystyrene
  done clear
  B)
   Teflon
  done clear
  C)
   Polyvinyl chloride
  done clear
  D)
   Nylon 6, 6
  done clear
  E)
   Novalac
  done clear
  View Answer play_arrow

• question_answer119) Which set is the correct pairing set (or contains complementary pairs) responsible for the structure of DNA? (A-adenine, G-guanine, C-cytosine, T-thymine, U-uracil)
  A)
   A-T, G-C
  done clear
  B)
   A-C, G-T
  done clear
  C)
   A-G, C-T
  done clear
  D)
   A-U, G-C
  done clear
  E)
   T-U, G-C
  done clear
  View Answer play_arrow

• question_answer120) Barbituric acid and its derivatives are well known as:
  A)
   tranquilizers    
  done clear
  B)
          antiseptics
  done clear
  C)
   analgesics      
  done clear
  D)
          antipyretics
  done clear
  E)
   antibiotic
  done clear
  View Answer play_arrow

• question_answer121) If\[f(x)={{\log }_{x}}({{\log }_{e}}x),\]then\[f(x)\]at\[x=e\]is equal to:
  A)
   1                                            
  done clear
  B)
   2                            
  done clear
  C)
   0                            
  done clear
  D)
          \[e\]
  done clear
  E)
   \[1/e\]
  done clear
  View Answer play_arrow

• question_answer122) The number of terms in the expansion of \[{{(a+b+c)}^{10}}\]is:
  A)
   11
  done clear
  B)
                                          21
  done clear
  C)
   55                         
  done clear
  D)
          66
  done clear
  E)
   44
  done clear
  View Answer play_arrow

• question_answer123) For what value of\[\lambda ,\]the system of equations \[x+y+z=6,\text{ }x+2y+3z=10,\]\[x+2y+\lambda z=10\]is consistent?
  A)
   1            
  done clear
  B)
                          2
  done clear
  C)
   \[-1\]                   
  done clear
  D)
          3
  done clear
  E)
   \[-3\]
  done clear
  View Answer play_arrow

• question_answer124) Let\[f(x)\]be twice differentiable such that\[f(x)=-f(x),f(x)=g(x),\]where\[f(x)\]and\[f(x)\]represent the first and second derivatives of\[f(x)\]respectively. Also, if\[h(x)={{[f(x)]}^{2}}+{{[g(x)]}^{2}}\]and\[h(5)=5,\]then\[h(10)\]is equal to:
  A)
   3                                            
  done clear
  B)
   10
  done clear
  C)
   13                         
  done clear
  D)
          5
  done clear
  E)
   0
  done clear
  View Answer play_arrow

• question_answer125) A straight line through P (1, 2) is such that its intercept between the axes is bisected at P. Its equation is:
  A)
   \[x+y=-1\]         
  done clear
  B)
   \[x+y=3\]
  done clear
  C)
   \[x+2y=5\]     
  done clear
  D)
          \[2x+y=4\]
  done clear
  E)
   none of these
  done clear
  View Answer play_arrow

• question_answer126) The radius of any circle touching the lines \[3x-4y+5=0\]and\[6x-8y-9=0\]is:
  A)
   1.9                                        
  done clear
  B)
   0.95
  done clear
  C)
   2.9                        
  done clear
  D)
          1.45
  done clear
  E)
   1.95
  done clear
  View Answer play_arrow

• question_answer127) The point on the curve\[\sqrt{x}+\sqrt{y}=\sqrt{a},\]the normal at which is parallel to the\[x-\]axis, is:
  A)
   \[(0,0)\]                             
  done clear
  B)
   \[(0,a)\]
  done clear
  C)
   \[(a,0)\]             
  done clear
  D)
         \[(a,a)\]
  done clear
  E)
   \[(-a,a)\]
  done clear
  View Answer play_arrow

• question_answer128) If two circles of the same radius r and centres at (2,3) and (5,6) respectively cut orthogonally, then the value of r is:
  A)
   3                                            
  done clear
  B)
   2
  done clear
  C)
   1                            
  done clear
  D)
          5
  done clear
  E)
   6
  done clear
  View Answer play_arrow

• question_answer129) The equation to the sides of a triangle are \[x-3y=0,\text{ }4x+3y=5\]and\[3x+y=0\]. The line \[3x-4y=0\]passes through:
  A)
   the incentre    
  done clear
  B)
          the centroid
  done clear
  C)
   the orthocentre
  done clear
  D)
          the circumcentre
  done clear
  E)
   none of these
  done clear
  View Answer play_arrow

• question_answer130) For\[|x|<1,\]let\[y=1+x+{{x}^{2}}+.....\]to\[\infty ,\]then\[\frac{dy}{dx}-y\]is equal to:
  A)
   \[\frac{x}{y}\]                                  
  done clear
  B)
   \[\frac{{{x}^{2}}}{{{y}^{2}}}\]
  done clear
  C)
   \[\frac{x}{{{y}^{2}}}\]                   
  done clear
  D)
          \[x{{y}^{2}}\]
  done clear
  E)
   \[\frac{x-1}{{{y}^{2}}}\]
  done clear
  View Answer play_arrow

• question_answer131) If\[(-4,5)\]is one vertex and\[7x-y+8=0\]is one diagonal of a square, then the equation of the second diagonal is:
  A)
  \[x+3y=21\]       
  done clear
  B)
   \[2x-3y=7\]
  done clear
  C)
  \[x+7y=31\]    
  done clear
  D)
          \[2x+3y=21\]
  done clear
  E)
   \[x-3y=21\]
  done clear
  View Answer play_arrow

• question_answer132) The number of common tangents to two circles \[{{x}^{2}}+{{y}^{2}}=4\] and\[{{x}^{2}}+{{y}^{2}}-8x+12=0\]is:
  A)
   1                                            
  done clear
  B)
   2                            
  done clear
  C)
   5                            
  done clear
  D)
          4
  done clear
  E)
   3
  done clear
  View Answer play_arrow

• question_answer133) If\[y=lo{{g}^{n}}x,\]where\[lo{{g}^{n}}\]means\[log\text{ }log\text{ }log\text{ }...\](repeated n times), then \[x\text{ }log\text{ }x\text{ }lo{{g}^{2}}x\text{ }lo{{g}^{3}}x\text{ }...\text{ }lo{{g}^{n-1}}\text{ }x\text{ }lo{{g}^{n}}x\frac{dy}{dx}\] is equal to:
  A)
   \[\log x\]                           
  done clear
  B)
   \[x\]                    
  done clear
  C)
   \[\frac{1}{\log x}\]         
  done clear
  D)
          \[1\]
  done clear
  E)
   \[{{\log }^{n}}x\]
  done clear
  View Answer play_arrow

• question_answer134) The focus of the parabola\[{{y}^{2}}-x-2y+2=0\]is:
  A)
   (1/4, 0)                               
  done clear
  B)
   (1, 2)    
  done clear
  C)
          (5/4, 1)               
  done clear
  D)
          (3/4, 5/2)
  done clear
  E)
   (1, 5/4)
  done clear
  View Answer play_arrow

• question_answer135) The equation of the parabola with vertex at the origin and directrix\[y=2\]is:
  A)
   \[{{y}^{2}}=8x\]                              
  done clear
  B)
   \[{{y}^{2}}=-8x\]            
  done clear
  C)
          \[{{y}^{2}}=\sqrt{8}x\]     
  done clear
  D)
          \[{{x}^{2}}=8y\]
  done clear
  E)
   \[{{x}^{2}}=-8y\]
  done clear
  View Answer play_arrow

• question_answer136) The point on the curve\[x{{y}^{2}}=1\]that is nearest to the origin, is:
  A)
   (1, 1)
  done clear
  B)
   (4, 1/2)
  done clear
  C)
   (1/4, 2)
  done clear
  D)
   \[({{2}^{1/6}},{{(1/2)}^{1/12}})\]
  done clear
  E)
   \[({{(1/2)}^{1/3}},{{2}^{1/6}})\]
  done clear
  View Answer play_arrow

• question_answer137) The distance of the point A (2, 3, 4) from\[x-\]axis is:
  A)
   5                                            
  done clear
  B)
   \[\sqrt{13}\]     
  done clear
  C)
         \[2\sqrt{5}\]                      
  done clear
  D)
          \[5\sqrt{2}\]
  done clear
  E)
   none of these
  done clear
  View Answer play_arrow

• question_answer138) The     radius     of     the     circle \[{{x}^{2}}+{{y}^{2}}+{{z}^{2}}-2y-4z-11=0\]and \[x+2y+2z-15=0\]is:
  A)
   \[\sqrt{3}\]                                       
  done clear
  B)
  \[\sqrt{5}\]                        
  done clear
  C)
   \[\sqrt{7}\]                       
  done clear
  D)
         \[3\]
  done clear
  E)
   \[\sqrt{2}\]
  done clear
  View Answer play_arrow

• question_answer139) \[\int{{{x}^{2}}{{(ax+b)}^{-2}}dx}\]is equal to:
  A)
   \[\frac{2}{{{a}^{2}}}\left( x-\frac{b}{a}\log (ax+b) \right)+c\]
  done clear
  B)
   \[\frac{2}{{{a}^{2}}}\left( x-\frac{b}{a}\log (ax+b) \right)-\frac{{{x}^{2}}}{a(ax+b)}+c\]
  done clear
  C)
   \[\frac{2}{{{a}^{2}}}\left( x+\frac{b}{a}\log (ax+b) \right)+\frac{{{x}^{2}}}{a(ax+b)}+c\]
  done clear
  D)
   \[\frac{2}{{{a}^{2}}}\left( x+\frac{b}{a}\log (ax+b) \right)-\frac{{{x}^{2}}}{a(ax+b)}+c\]
  done clear
  E)
   \[\frac{2}{{{a}^{2}}}\left( x-\frac{b}{a}\log (ax+b) \right)+\frac{{{x}^{2}}}{a(ax+b)}+c\]
  done clear
  View Answer play_arrow

• question_answer140) If the co-ordinate of the vertices of a triangle ABC be\[A(-1,3,2),B(2,3,5)\]and \[C(3,5,-2),\] then\[\angle A\]is equal to:
  A)
   \[45{}^\circ \]                                  
  done clear
  B)
   \[60{}^\circ \]                  
  done clear
  C)
   \[90{}^\circ \]                  
  done clear
  D)
          \[30{}^\circ \]
  done clear
  E)
   \[135{}^\circ \]
  done clear
  View Answer play_arrow

• question_answer141) If\[\overrightarrow{a}+\overrightarrow{b}+\overrightarrow{c}=\overrightarrow{0}|\overrightarrow{a}|=3,|\overrightarrow{b}|=5\]and\[|\overrightarrow{c}|=7,\]then the angle between\[\overrightarrow{a}\]and\[\overrightarrow{b}\]is:
  A)
   0                                            
  done clear
  B)
   \[30{}^\circ \]                  
  done clear
  C)
   \[45{}^\circ \]                  
  done clear
  D)
          \[60{}^\circ \]
  done clear
  E)
   \[90{}^\circ \]
  done clear
  View Answer play_arrow

• question_answer142) If\[f(t)\]is an odd function, the\[\int_{0}^{x}{f(t)}\,dt\]is:
  A)
   an odd function
  done clear
  B)
   an even function
  done clear
  C)
   neither even nor odd
  done clear
  D)
   0
  done clear
  E)
   1     
  done clear
  View Answer play_arrow

• question_answer143) The projection of\[\hat{i}+3\text{ }\hat{j}+\hat{k}\]on\[2\hat{i}-3\text{ }\hat{j}+6\hat{k}\]is:
  A)
   1/7                                       
  done clear
  B)
   \[-1/7\]                              
  done clear
  C)
   7                            
  done clear
  D)
          \[-7\]
  done clear
  E)
   1
  done clear
  View Answer play_arrow

• question_answer144) If\[\overrightarrow{a}\times \overrightarrow{b}=0\]and\[\overrightarrow{a}.\overrightarrow{b}=0\]then:
  A)
   \[\overrightarrow{a}\bot \overrightarrow{b}\]                
  done clear
  B)
   \[\overrightarrow{a}|\,|\overrightarrow{b}\]  
  done clear
  C)
          \[\overrightarrow{a}=0\]and\[\overrightarrow{b}=\overrightarrow{0}\]
  done clear
  D)
          \[\overrightarrow{a}=\overrightarrow{0}\]and\[\overrightarrow{b}=\overrightarrow{0}\]
  done clear
  E)
   cannot be determined
  done clear
  View Answer play_arrow

• question_answer145) If the area bounded by the parabola\[y=2-{{x}^{2}}\]and the line\[x+y=0\]is A sq unit, then A equals:
  A)
   1/2                                       
  done clear
  B)
   1/3                       
  done clear
  C)
   2/9                       
  done clear
  D)
          9/2
  done clear
  E)
   9
  done clear
  View Answer play_arrow

• question_answer146) The points\[A(4,5,1),B(0,-1,-1),C(3,9,4)\]and \[D(-4,4,4)\]are:
  A)
   collinear             
  done clear
  B)
   coplanar             
  done clear
  C)
          non-coplanar   
  done clear
  D)
          non-collinear
  done clear
  E)
   non-collinear and non-coplanar
  done clear
  View Answer play_arrow

• question_answer147) \[{{(\overrightarrow{a}\times \overrightarrow{b})}^{2}}\]is equal to:
  A)
   \[\overset{{{\to }^{2}}}{\mathop{a}}\,+\overset{{{\to }^{2}}}{\mathop{b}}\,-(\overrightarrow{a}.\overrightarrow{b})\]
  done clear
  B)
   \[\overset{{{\to }^{2}}}{\mathop{a}}\,+\overset{{{\to }^{2}}}{\mathop{b}}\,-{{(\overrightarrow{a}.\overrightarrow{b})}^{2}}\]
  done clear
  C)
   \[\overset{{{\to }^{2}}}{\mathop{a}}\,+\overset{{{\to }^{2}}}{\mathop{b}}\,-2\,\,\overrightarrow{a}\,\,.\,\,\overrightarrow{b}\]
  done clear
  D)
   \[\overset{{{\to }^{2}}}{\mathop{a}}\,+\overset{{{\to }^{2}}}{\mathop{b}}\,-2\,\,\overrightarrow{a}\,\,.\,\,\overrightarrow{b}\]
  done clear
  E)
   none of the above
  done clear
  View Answer play_arrow

• question_answer148) Let F denotes the family of ellipses whose centre is at the origin and major axis is the y-axis. Then, equation of the family F is:
  A)
   \[\frac{{{d}^{2}}y}{d{{x}^{2}}}+\frac{dy}{dx}\left( x\frac{dy}{dx}-y \right)=0\]
  done clear
  B)
   \[xy\frac{{{d}^{2}}y}{d{{x}^{2}}}-\frac{dy}{dx}\left( x\frac{dy}{dx}-y \right)=0\]
  done clear
  C)
   \[xy\frac{{{d}^{2}}y}{d{{x}^{2}}}+\frac{dy}{dx}\left( x\frac{dy}{dx}-y \right)=0\]
  done clear
  D)
   \[\frac{{{d}^{2}}y}{d{{x}^{2}}}-\frac{dy}{dx}\left( x\frac{dy}{dx}-y \right)=0\]
  done clear
  E)
   \[xy\frac{{{d}^{2}}y}{d{{x}^{2}}}+\left( x\frac{dy}{dx}-y \right)=0\]
  done clear
  View Answer play_arrow

• question_answer149) The value of \[\left( \cos \frac{\pi }{2}+i\sin \frac{\pi }{2} \right)\left[ \cos \left( \frac{\pi }{{{2}^{2}}} \right)+i\sin \left( \frac{\pi }{{{2}^{2}}} \right) \right]\] \[\left[ \cos \left( \frac{\pi }{{{2}^{3}}} \right)+i\sin \left( \frac{\pi }{{{2}^{3}}} \right) \right].....\infty \]is:
  A)
   \[-1\]                                   
  done clear
  B)
   \[1\]                    
  done clear
  C)
   \[0\]                    
  done clear
  D)
          \[\sqrt{2}\]
  done clear
  E)
   \[-\sqrt{2}\]
  done clear
  View Answer play_arrow

• question_answer150) If\[x+\frac{1}{x}=2\sin \alpha ,y+\frac{1}{y}=2\cos \beta ,\]then\[{{x}^{3}}{{y}^{3}}+\frac{1}{{{x}^{3}}{{y}^{3}}}\]is:
  A)
   \[2\cos 3(\beta -\alpha )\]         
  done clear
  B)
   \[2\cos 3(\beta +\alpha )\]
  done clear
  C)
                          \[2\sin 3(\beta -\alpha )\]
  done clear
  D)
          \[2\sin 3(\beta +\alpha )\]
  done clear
  E)
   \[\sin 3(\beta -\alpha )\]
  done clear
  View Answer play_arrow

• question_answer151) Solution       of       the       equation\[x{{\left( \frac{dy}{dx} \right)}^{2}}+2\sqrt{xy}\frac{dy}{dx}+y=0\]is:
  A)
   \[x+y=a\]          
  done clear
  B)
   \[\sqrt{x}-\sqrt{y}=\sqrt{a}\]
  done clear
  C)
          \[{{x}^{2}}+{{y}^{2}}={{a}^{2}}\]   
  done clear
  D)
          \[\sqrt{x}+\sqrt{y}=\sqrt{a}\]
  done clear
  E)
   \[{{x}^{2}}-{{y}^{2}}={{a}^{2}}\]
  done clear
  View Answer play_arrow

• question_answer152) A bag contains 5 white and 3 black balls and 4 balls are successively drawn out and not replaced. The probability that they are alternately of different colours, is:
  A)
   1/196                                   
  done clear
  B)
   2/7                       
  done clear
  C)
   1/7                       
  done clear
  D)
          13/56
  done clear
  E)
   3/7  
  done clear
  View Answer play_arrow

• question_answer153) If \[\underset{x\to a}{\mathop{\lim }}\,\frac{{{a}^{x}}-{{x}^{a}}}{{{x}^{x}}-{{a}^{a}}}=-1,\]then a equals to:
  A)
   1        
  done clear
  B)
                                          0                            
  done clear
  C)
   e                           
  done clear
  D)
         \[(1/e)\]
  done clear
  E)
   \[\infty \]
  done clear
  View Answer play_arrow

• question_answer154) \[\underset{x\to 0}{\mathop{\lim }}\,\frac{\tan x-\sin x}{{{x}^{3}}}\]is equal to:
  A)
   0    
  done clear
  B)
                                          1                            
  done clear
  C)
   1/2                       
  done clear
  D)
         \[-1/2\]
  done clear
  E)
   \[\infty \]
  done clear
  View Answer play_arrow

• question_answer155) \[\underset{x\to a}{\mathop{\lim }}\,\frac{\log (x-a)}{\log ({{e}^{x}}-{{e}^{a}})}\]is equal to:
  A)
   0                                            
  done clear
  B)
   1                            
  done clear
  C)
          a                            
  done clear
  D)
          does not exist
  done clear
  E)
   \[-a\]
  done clear
  View Answer play_arrow

• question_answer156) If\[f(x)=|x{{|}^{3}},\] then\[f(0)\] equals:
  A)
   0                                            
  done clear
  B)
   1/2                       
  done clear
  C)
          \[-1\]                   
  done clear
  D)
          \[-1/2\]
  done clear
  E)
   none of these
  done clear
  View Answer play_arrow

• question_answer157) \[\int{{{e}^{-\log x}}}dx\]is equal to:
  A)
   \[{{e}^{-\log x}}+c\]                      
  done clear
  B)
   \[-x{{e}^{-\log x}}+c\]  
  done clear
  C)
          \[{{e}^{\log x}}+c\]       
  done clear
  D)
          \[\log x+c\]
  done clear
  E)
   \[\log |x|+c\]
  done clear
  View Answer play_arrow

• question_answer158) The area cut off by the latus rectum from the parabola\[{{y}^{2}}=4ax\]is:
  A)
   \[(8/3)\text{ }a\text{ }sq\text{ }unit\]                  
  done clear
  B)
   \[(8/3)\,\sqrt{a}\,sq\,\] unit
  done clear
  C)
                          \[(3/8)\text{ }{{a}^{2}}\text{ }sq\text{ }unit\]   
  done clear
  D)
   \[(8/3)\text{ }{{a}^{3}}sq\text{ }unit\]
  done clear
  E)
   \[(8/3)\text{ }{{a}^{2}}\text{ }sq\text{ }unit\]
  done clear
  View Answer play_arrow

• question_answer159) The   solution   of  differential   equation \[(x+y)(dx-dy)=dx+dy\]is:
  A)
   \[x-y=k{{e}^{x-y}}\]      
  done clear
  B)
   \[x+y=k{{e}^{x+y}}\]
  done clear
  C)
          \[x+y=k(x-y)\]
  done clear
  D)
          \[x-y=k{{e}^{x+y}}\]
  done clear
  E)
   \[x+y=k{{e}^{x-y}}\]
  done clear
  View Answer play_arrow

• question_answer160) In how many ways can 8 students be arranged in a row?
  A)
   \[8!\]                   
  done clear
  B)
          \[7!\]                   
  done clear
  C)
   8                            
  done clear
  D)
          7
  done clear
  E)
   \[2\times 7!\]
  done clear
  View Answer play_arrow

• question_answer161) If the third term of a GP is P, then the product of the first 5 terms of the GP is:
  A)
   \[{{P}^{3}}\]                                     
  done clear
  B)
   \[{{P}^{2}}\]                     
  done clear
  C)
   \[{{P}^{10}}\]                   
  done clear
  D)
          \[{{P}^{4}}\]
  done clear
  E)
   \[{{P}^{5}}\]
  done clear
  View Answer play_arrow

• question_answer162) The sum to n terms of the series\[\frac{4}{3}+\frac{10}{9}+\frac{28}{27}+.....\]is:
  A)
   \[\frac{{{3}^{n}}(2n+1)+1}{2({{3}^{n}})}\]           
  done clear
  B)
   \[\frac{{{3}^{n}}(2n+1)-1}{2({{3}^{n}})}\]            
  done clear
  C)
   \[\frac{{{3}^{n}}n-1}{2({{3}^{n}})}\]       
  done clear
  D)
          \[\frac{{{3}^{n}}-1}{2}\]
  done clear
  E)
   \[\frac{{{3}^{n}}-n}{2({{3}^{n}})}\]
  done clear
  View Answer play_arrow

• question_answer163) If\[\alpha \]and\[\beta \]are the solutions of the quadratic equation\[a{{x}^{2}}+bx+c=0\]such that\[\beta ={{\alpha }^{1/3}},\]then:
  A)
   \[{{(ac)}^{1/3}}+{{(ab)}^{1/3}}+c=0\]
  done clear
  B)
   \[{{({{a}^{3}}b)}^{1/4}}+{{(a{{b}^{3}})}^{1/4}}+c=0\]
  done clear
  C)
   \[{{({{a}^{3}}c)}^{1/4}}+{{(a{{c}^{3}})}^{1/4}}+b=0\]
  done clear
  D)
   \[{{({{a}^{4}}c)}^{1/3}}+{{(a{{c}^{4}})}^{1/3}}+b=0\]
  done clear
  E)
   \[{{({{a}^{3}}c)}^{1/4}}-{{(a{{c}^{3}})}^{1/4}}+b=0\]
  done clear
  View Answer play_arrow

• question_answer164) \[^{20}{{C}_{4}}+{{2.}^{20}}{{C}_{3}}{{+}^{20}}{{C}_{2}}{{-}^{22}}{{C}_{18}}\]is equal to:
  A)
   0                                            
  done clear
  B)
   1242     
  done clear
  C)
          7315                     
  done clear
  D)
          6345
  done clear
  E)
   3340
  done clear
  View Answer play_arrow

• question_answer165) If \[x=\frac{\left[ \begin{align}   & 729+6(2)(243)+15(4)(81)+20(8)(27) \\  & +15(16)(9)+6(32)3+64 \\ \end{align} \right]}{1+4(4)+6(16)+4(64)+256}\] then \[\sqrt{x}-\frac{1}{\sqrt{x}}\]is equal to:
  A)
   0.2                                        
  done clear
  B)
   4.8                        
  done clear
  C)
   1.02                      
  done clear
  D)
          5.2
  done clear
  E)
   25
  done clear
  View Answer play_arrow

• question_answer166) Along a road lie an odd number of stones placed at intervals of 10 m. These stones have to be assembled around the middle stone. A person can carry only one stone at a time. A man started the job with one of the end stones by carrying them in succession. In carrying all the stones, the man covered a total distance of 3 km. Then the total number of stones is:
  A)
   20         
  done clear
  B)
                          25                         
  done clear
  C)
   12                         
  done clear
  D)
          24
  done clear
  E)
   50
  done clear
  View Answer play_arrow

• question_answer167) If \[a=1+2+4+...\]to n terms, \[b=1+3+9+...\]to n terms and \[c=1+5+25+...\]to n terms, then \[\left| \begin{matrix}    a & 2b & 4c  \\    2 & 2 & 2  \\    {{2}^{n}} & {{3}^{n}} & {{5}^{n}}  \\ \end{matrix} \right|\]equals:
  A)
   \[{{(30)}^{n}}\]               
  done clear
  B)
   \[{{(10)}^{n}}\]
  done clear
  C)
   \[0\]                    
  done clear
  D)
          \[{{2}^{n}}+{{3}^{n}}+{{5}^{n}}\]
  done clear
  E)
   none of these
  done clear
  View Answer play_arrow

• question_answer168) The matrix \[\left| \begin{matrix}    5 & 10 & 3  \\    -2 & -4 & 6  \\    -1 & -2 & b  \\ \end{matrix} \right|\]is a singular matrix, if b is equal to:
  A)
   \[-3\]                                   
  done clear
  B)
   3                            
  done clear
  C)
   0                            
  done clear
  D)
          for any value of b
  done clear
  E)
   for no value of b
  done clear
  View Answer play_arrow

• question_answer169) Let N be the number of quadratic equations with coefficients from {0, 1, 2, ..., 9} such that zero is a solution of each equation. Then the value of N is:
  A)
   infinite                
  done clear
  B)
          29                         
  done clear
  C)
   90                         
  done clear
  D)
          900
  done clear
  E)
   81
  done clear
  View Answer play_arrow

• question_answer170) For non-singular square matrices A, B and C of the same order,\[{{(A{{B}^{-1}}C)}^{-1}}\]is equal to:
  A)
   \[{{A}^{-1}}B{{C}^{-1}}\]                             
  done clear
  B)
   \[{{C}^{-1}}{{B}^{-1}}{{A}^{-1}}\]            
  done clear
  C)
   \[CB{{A}^{-1}}\]              
  done clear
  D)
          \[{{C}^{-1}}B{{A}^{-1}}\]
  done clear
  E)
   \[{{C}^{-1}}BA\]
  done clear
  View Answer play_arrow

• question_answer171) The points\[(1,1),(-5,5)\]and\[(13,\lambda )\]lie on the same straight line, if\[\lambda \]is equal to:
  A)
   7                                            
  done clear
  B)
   \[-7\]                   
  done clear
  C)
   \[\pm 7\]                           
  done clear
  D)
          0
  done clear
  E)
   14
  done clear
  View Answer play_arrow

• question_answer172) If\[n=1,\text{ }2,\text{ }3,\text{ }....\]then\[\cos \alpha \cos 2\alpha \cos 4\alpha .....\cos {{2}^{n-1}}\alpha \] is equal to:
  A)
   \[\frac{\sin 2n\alpha }{2n\sin \alpha }\]                               
  done clear
  B)
   \[\frac{\sin {{2}^{n}}\alpha }{{{2}^{n}}\sin {{2}^{n-1}}\alpha }\]
  done clear
  C)
          \[\frac{\sin {{4}^{n-1}}\alpha }{{{4}^{n-1}}\sin \alpha }\]              
  done clear
  D)
          \[\frac{\sin {{2}^{n}}\alpha }{{{2}^{n}}\sin \alpha }\]
  done clear
  E)
   none of these
  done clear
  View Answer play_arrow

• question_answer173) If the lines \[3x+4y+1=0,\text{ }5x+\lambda y+3=0\] and \[2x+y-1=0\]are concurrent, then \[\lambda \] is equal to:
  A)
   \[-8\]                                   
  done clear
  B)
   8                            
  done clear
  C)
   4                            
  done clear
  D)
          \[-4\]
  done clear
  E)
   none of these
  done clear
  View Answer play_arrow

• question_answer174) If the equation\[k{{x}^{2}}-2xy-{{y}^{2}}-2x+2y=0\]represents a pair of lines, then k is equal to:
  A)
   2                                            
  done clear
  B)
   \[-2\]                   
  done clear
  C)
   \[-5\]                   
  done clear
  D)
          5
  done clear
  E)
   3
  done clear
  View Answer play_arrow

• question_answer175) Let \[A=\left[ \begin{matrix}    {{\cos }^{2}}\theta  & \sin \theta \cos \theta   \\    \cos \theta \sin \theta  & {{\sin }^{2}}\theta   \\ \end{matrix} \right]\]and\[B=\left[ \begin{matrix}   {{\cos }^{2}}\phi  & \sin \phi \cos \phi   \\    \cos \phi \sin \phi  & {{\sin }^{2}}\phi   \\ \end{matrix} \right]\]then\[AB=0\]if:
  A)
   \[\theta =n\phi ,n=0,1,2,....\]
  done clear
  B)
   \[\theta +\phi =n\pi ,n=0,1,2,....\]
  done clear
  C)
   \[\theta =\phi +(2n+1)\frac{\pi }{2},n=0,1,2,....\]
  done clear
  D)
   \[\theta =\phi +n\frac{\pi }{2},n=0,1,2,....\]
  done clear
  E)
   \[\theta =\phi +3n\frac{\pi }{2},n=0,1,2,....\]
  done clear
  View Answer play_arrow

• question_answer176) If the area of the circle \[4{{x}^{2}}+4{{y}^{2}}-8x+16y+k=0\]is\[9\pi \]sq unit, then the value of k is:
  A)
   4 sq unit       
  done clear
  B)
          16 sq unit           
  done clear
  C)
          \[-16\]sq unit     
  done clear
  D)
          \[\pm 16\] sq unit
  done clear
  E)
   none of these
  done clear
  View Answer play_arrow

• question_answer177) If a focal chord of the parabola\[{{y}^{2}}=ax\]is \[2x-y-8=0,\]then the equation of the directrix is:
  A)
   \[x+4=0\]       
  done clear
  B)
          \[x-4=0\]           
  done clear
  C)
          \[y-4=0\]       
  done clear
  D)
          \[y+4=0\]
  done clear
  E)
   none of these
  done clear
  View Answer play_arrow

• question_answer178) Let\[X=\left[ \begin{matrix}    {{x}_{1}}  \\    {{x}_{2}}  \\    {{x}_{3}}  \\ \end{matrix} \right],A=\left[ \begin{matrix}    1 & -1 & 2  \\    2 & 0 & 1  \\    3 & 2 & 1  \\ \end{matrix} \right]\]and\[B=\left[ \begin{matrix}    3  \\    1  \\    4  \\ \end{matrix} \right]\]. If\[AX=B,\]then\[X\]is equal to:
  A)
   \[\left[ \begin{matrix}    1  \\    2  \\    3  \\ \end{matrix} \right]\]                                   
  done clear
  B)
   \[\left[ \begin{matrix}    -1  \\    -2  \\    3  \\ \end{matrix} \right]\]   
  done clear
  C)
          \[\left[ \begin{matrix}    -1  \\    -2  \\    -3  \\ \end{matrix} \right]\]   
  done clear
  D)
          \[\left[ \begin{matrix}    -1  \\    2  \\    3  \\ \end{matrix} \right]\]
  done clear
  E)
   \[\left[ \begin{matrix}    0  \\    2  \\    1  \\ \end{matrix} \right]\]
  done clear
  View Answer play_arrow

• question_answer179) A line make angles of\[45{}^\circ \]and\[60{}^\circ \]with the \[x-\]axis and the z-axis respectively. The angle made by it with y-axis is:
  A)
   \[30{}^\circ \,or\text{ }150{}^\circ \]    
  done clear
  B)
   \[60{}^\circ \,or\text{ }120{}^\circ \]
  done clear
  C)
   \[45{}^\circ \,or\text{ }135{}^\circ \]  
  done clear
  D)
          \[90{}^\circ \]
  done clear
  E)
   none of these
  done clear
  View Answer play_arrow

• question_answer180) If\[a=\frac{\pi }{18}\]rad then\[\cos a+\cos 2a+...+\cos 18a\] is equal to:
  A)
   0                            
  done clear
  B)
          \[-1\]                   
  done clear
  C)
   1                            
  done clear
  D)
          \[\pm 1\]
  done clear
  E)
   none of these
  done clear
  View Answer play_arrow

• question_answer181) If\[\sec \theta +\tan \theta =k,\cos \theta \]equals to:
  A)
   \[\frac{{{k}^{2}}+1}{2k}\]                           
  done clear
  B)
   \[\frac{2k}{{{k}^{2}}+1}\]           
  done clear
  C)
          \[\frac{k}{{{k}^{2}}+1}\]              
  done clear
  D)
          \[\frac{k}{{{k}^{2}}-1}\]
  done clear
  E)
   none of these
  done clear
  View Answer play_arrow

• question_answer182) \[\underset{x\to \frac{\pi }{6}}{\mathop{\lim }}\,\frac{2{{\sin }^{2}}x+\sin x-1}{2{{\sin }^{2}}x-3\sin x+1}\]is equal to:
  A)
   3                            
  done clear
  B)
          \[-3\]                   
  done clear
  C)
   6                            
  done clear
  D)
          0
  done clear
  E)
   9
  done clear
  View Answer play_arrow

• question_answer183) If the function\[f(x)\]is defined by \[f(x)=a+bx\]and\[{{f}^{r}}=fff\text{ }...\](repeated r times), then \[{{f}^{r}}(x)\]is equal to:
  A)
   \[a+{{b}^{r}}x\]              
  done clear
  B)
          \[ar+{{b}^{r}}x\]             
  done clear
  C)
                          \[ar+b{{x}^{r}}\]             
  done clear
  D)
          \[a({{b}^{r}}-1)+{{b}^{r}}x\]
  done clear
  E)
   \[a\left( \frac{{{b}^{r}}-1}{b-1} \right)+{{b}^{r}}x\]
  done clear
  View Answer play_arrow

• question_answer184) If a particle is moving such that the velocity acquired is proportional to the square root of the distance covered, then its acceleration is:
  A)
   a constant      
  done clear
  B)
          \[\propto {{s}^{2}}\]     
  done clear
  C)
          \[\propto \frac{1}{{{s}^{2}}}\]                  
  done clear
  D)
          \[\propto s\]
  done clear
  E)
   \[\propto \frac{1}{s}\]
  done clear
  View Answer play_arrow

• question_answer185) If \[f(x)=\frac{1-x}{1+x}(x\ne -1),\]then\[{{f}^{-1}}(x)\]W equals to:
  A)
   \[f(x)\]
  done clear
  B)
          \[\frac{1}{f(x)}\]             
  done clear
  C)
          \[-f(x)\]              
  done clear
  D)
          \[-\frac{1}{f(x)}\]
  done clear
  E)
   not defined
  done clear
  View Answer play_arrow

• question_answer186) Domain of the function\[f(x)={{\sin }^{-1}}({{\log }_{2}}x)\]in the set of real numbers is:
  A)
   \[\{x:1\le x\le 2\}\]
  done clear
  B)
          \[\{x:1\le x\le 3\}\]
  done clear
  C)
          \[\{x:-1\le x\le 2\}\]
  done clear
  D)
          \[\left\{ x:\frac{1}{2}\le x\le 2 \right\}\]
  done clear
  E)
   \[\left\{ x:-\frac{1}{2}\le x\le 2 \right\}\]
  done clear
  View Answer play_arrow

• question_answer187) If \[\omega \] is a complex cube root of unity, then \[\frac{a+b\omega +c{{\omega }^{2}}}{c+a\omega +b{{\omega }^{2}}}+\frac{c+a\omega +b{{\omega }^{2}}}{a+b\omega +c{{\omega }^{2}}}+\frac{b+c\omega +a{{\omega }^{2}}}{b+c{{\omega }^{4}}+a{{\omega }^{5}}}\] is equal to:
  A)
   \[1\]                    
  done clear
  B)
          \[\omega \]                      
  done clear
  C)
   \[{{\omega }^{2}}\]                       
  done clear
  D)
          \[-1\]
  done clear
  E)
   0
  done clear
  View Answer play_arrow

• question_answer188) If\[\alpha ,\beta \]and\[\gamma \]are angles such that\[\tan \alpha +\tan \beta +\tan \gamma =\tan \alpha .\tan \beta .\tan \gamma \]and\[x=\cos \alpha +i\sin \alpha ,y=\cos \beta +i\sin \beta \]and\[z=\cos \gamma +i\sin \gamma ,\]then\[xyz\]is equal to:
  A)
   1, but not\[-1\]   
  done clear
  B)
         \[-1\], but not 1
  done clear
  C)
          \[1\]or\[-1\]                     
  done clear
  D)
          0
  done clear
  E)
   \[i\]
  done clear
  View Answer play_arrow

• question_answer189) If\[\alpha \]and\[\beta \]are complex cube roots of unity and \[x=a\alpha +b\beta ,\text{ }y=a+b,\text{ }z=\alpha \beta +b\alpha ,\]then\[xyz\] is equal to:
  A)
   \[a+b\]               
  done clear
  B)
          \[a-b\]
  done clear
  C)
   \[{{a}^{2}}+{{c}^{2}}\]                  
  done clear
  D)
          \[{{a}^{2}}-{{b}^{2}}\]
  done clear
  E)
   \[{{a}^{3}}+{{b}^{3}}\]
  done clear
  View Answer play_arrow

• question_answer190) If a, b and c are distinct positive real numbers in AP, then the roots of the equation \[a{{x}^{2}}+2bx+c=0\]are:
  A)
   imaginary
  done clear
  B)
   rational and equal
  done clear
  C)
   rational and distinct
  done clear
  D)
   irrational
  done clear
  E)
   real, may be rational or irrational
  done clear
  View Answer play_arrow

• question_answer191) If a, b and c are in AP, then which one of the following is not true?
  A)
   \[\frac{k}{a},\frac{k}{b}\]and\[\frac{k}{c}\]are in HP
  done clear
  B)
   \[a+k,\text{ }b+k\] and\[c+k\] are in AP
  done clear
  C)
   \[ka,kb\] and\[kc\]are in AP
  done clear
  D)
   \[{{a}^{2}},\text{ }{{b}^{2}}\]and\[{{c}^{2}}\]are in AP
  done clear
  E)
  \[a+b,\text{ }c+a\]and\[b+c\]are in AP
  done clear
  View Answer play_arrow

• question_answer192) If\[{{z}_{1}},{{z}_{2}}\]and\[{{z}_{3}}\]are any three complex numbers, then the fourth vertex of the parallelogram whose three vertices are\[{{z}_{1}},{{z}_{2}}\]and\[{{z}_{3}}\]taken in order, is:
  A)
   \[{{z}_{1}}-{{z}_{2}}+{{z}_{3}}\]
  done clear
  B)
          \[{{z}_{1}}+{{z}_{2}}+{{z}_{3}}\]              
  done clear
  C)
          \[\frac{1}{3}({{z}_{1}}-{{z}_{2}}+{{z}_{3}})\]
  done clear
  D)
          \[\frac{1}{3}({{z}_{1}}+{{z}_{2}}-{{z}_{3}})\]
  done clear
  E)
   \[\frac{1}{3}({{z}_{1}}-{{z}_{2}}-{{z}_{3}})\]
  done clear
  View Answer play_arrow

• question_answer193) \[\sqrt{4},\sqrt[4]{4},\sqrt[8]{4},\sqrt[16]{4},....\]to\[\infty \]are roots of the equation:
  A)
   \[{{x}^{2}}-4=0\]     
  done clear
  B)
          \[{{x}^{2}}-4x+6=0\]
  done clear
  C)
                          \[{{x}^{2}}-5x+4=0\]
  done clear
  D)
          \[{{x}^{2}}-3x+2=0\]
  done clear
  E)
   \[{{x}^{2}}-x=0\]
  done clear
  View Answer play_arrow

• question_answer194) If\[{{a}_{1}},{{a}_{2}},{{a}_{3}},.....,{{a}_{n}}\]are the n arithmetic means between a and b, then\[2\sum\limits_{i=1}^{n}{{{a}_{i}}}\]equals:
  A)
   \[ab\]                  
  done clear
  B)
   \[n(a+b)\]
  done clear
  C)
   \[nab\]                               
  done clear
  D)
   \[\frac{(a+b)}{n}\]
  done clear
  E)
   \[\frac{n(a+b)}{ab}\]
  done clear
  View Answer play_arrow

• question_answer195) Let a, b be the solutions of\[{{x}^{2}}+px+1=0\]and c, d be the solutions of\[{{x}^{2}}+qx+1=0\]. If \[(a-c)(b-c)\]and\[(a+d)(b+d)\]are the solutions of\[{{x}^{2}}+ax+\beta =0,\]then \[\beta \] equals:
  A)
   \[p+q\]               
  done clear
  B)
          \[p-q\]
  done clear
  C)
   \[{{p}^{2}}+{{q}^{2}}\]         
  done clear
  D)
          \[{{p}^{2}}-{{q}^{2}}\]
  done clear
  E)
   \[{{q}^{2}}-{{p}^{2}}\]
  done clear
  View Answer play_arrow

• question_answer196) The \[x-\]co-ordinate of the incentre of the triangle where the mid points of the sides are (0, 1), (1,1) and (1, 0), is:
  A)
   \[2+\sqrt{2}\]  
  done clear
  B)
          \[1+\sqrt{2}\]
  done clear
  C)
   \[2-\sqrt{2}\]   
  done clear
  D)
          \[1-\sqrt{2}\]
  done clear
  E)
   \[3-\sqrt{2}\]
  done clear
  View Answer play_arrow

• question_answer197) Which one of the following is true?
  A)
   \[\sin ({{\cos }^{-1}}x)=\cos ({{\sin }^{-1}}x)\]
  done clear
  B)
   \[\sec ({{\tan }^{-1}}x)=\tan ({{\sec }^{-1}}x)\]
  done clear
  C)
   \[\cos ({{\tan }^{-1}}x)=\tan ({{\cos }^{-1}}x)\]
  done clear
  D)
   \[\tan ({{\sin }^{-1}}x)=\sin ({{\tan }^{-1}}x)\]
  done clear
  E)
   all of these
  done clear
  View Answer play_arrow

• question_answer198) If\[{{\tan }^{-1}}a+{{\tan }^{-1}}b={{\sin }^{-1}}1-{{\tan }^{-1}}c,\]then:
  A)
   \[a+b+c=abc\]
  done clear
  B)
   \[ab+bc+ca=abc\]
  done clear
  C)
   \[\frac{1}{a}+\frac{1}{b}+\frac{1}{c}-\frac{1}{abc}=0\]
  done clear
  D)
   \[ab+bc+ca=a+b+c\]
  done clear
  E)
   none of the above
  done clear
  View Answer play_arrow

• question_answer199) Two consecutive sides of a parallelogram are \[4x+5y=0\] and\[7x+2y=0\]. One diagonal of the parallelogram is\[11x+7y=9\]. If the other diagonal is\[ax+by+c=0,\]then:
  A)
   \[a=-1,b=-1,c=2\]
  done clear
  B)
   \[a=1,b=-1,c=0\]
  done clear
  C)
   \[a=-1,b=-1,c=0\]
  done clear
  D)
   \[a=1,b=1,c=0\]
  done clear
  E)
   \[a=-1,b=-1,c=1\]
  done clear
  View Answer play_arrow

• question_answer200) The number of values of \[\theta \] in the interval\[[-\pi ,\pi ]\]satisfying the equation\[cos\theta +sin2\theta =0\]is:
  A)
   1                            
  done clear
  B)
          2
  done clear
  C)
   3                            
  done clear
  D)
          4
  done clear
  E)
   many
  done clear
  View Answer play_arrow

• question_answer201) From a set of 100 cards numbered 1 to 100, one card is drawn at random. The probability that the number obtained on the card is divisible by 6 or 8 but not by 24, is:
  A)
   \[\frac{6}{25}\]               
  done clear
  B)
          \[\frac{1}{4}\]
  done clear
  C)
   \[\frac{1}{6}\]                  
  done clear
  D)
          \[\frac{2}{5}\]
  done clear
  E)
   \[\frac{4}{5}\]
  done clear
  View Answer play_arrow

• question_answer202) If the line\[x+y-1=0\]is a tangent to the parabola\[{{y}^{2}}-y+x=0,\]then the point of contact is:
  A)
   (0, 1)                    
  done clear
  B)
          \[(1,0)\]
  done clear
  C)
   \[(0,-1)\]            
  done clear
  D)
          \[(-1,0)\]
  done clear
  E)
   \[(0,-1)\]
  done clear
  View Answer play_arrow

• question_answer203) If\[f(x)=\left\{ \begin{matrix}    \frac{2x-1}{\sqrt{1+x}-1}, & -1\le x<\infty ,x\ne 0  \\    k, & x=0  \\ \end{matrix} \right.\] is continuous everywhere, then k is equal to :
  A)
   \[\frac{1}{2}\log 2\]      
  done clear
  B)
           \[\log 4\]
  done clear
  C)
   \[\log 8\]           
  done clear
  D)
          \[\log 2\]
  done clear
  E)
   none of these
  done clear
  View Answer play_arrow

• question_answer204) If\[\sec \left( \frac{{{x}^{2}}-{{y}^{2}}}{{{x}^{2}}+{{y}^{2}}} \right)={{e}^{a}},\]then\[\frac{dy}{dx}\]is equal to:
  A)
   \[\frac{{{y}^{2}}}{{{x}^{2}}}\]                    
  done clear
  B)
          \[\frac{y}{x}\]
  done clear
  C)
   \[\frac{x}{y}\]                  
  done clear
  D)
          \[\frac{{{x}^{2}}-{{y}^{2}}}{{{x}^{2}}+{{y}^{2}}}\]
  done clear
  E)
   \[0\]
  done clear
  View Answer play_arrow

• question_answer205) The curve represented by the equation \[4{{x}^{2}}+16{{y}^{2}}-24x-32y-12=0\]is:
  A)
   a parabola
  done clear
  B)
   a pair of straight lines
  done clear
  C)
   an ellipse with eccentricity ½
  done clear
  D)
   an ellipse with eccentricity\[\sqrt{3}/2\]
  done clear
  E)
   a hyperbola with eccentricity 3/2
  done clear
  View Answer play_arrow

• question_answer206) It\[{{\sin }^{-1}}x+{{\sin }^{-1}}y=\frac{\pi }{2},\]then\[\frac{dy}{dx}\]is equal to:
  A)
   \[\frac{x}{y}\]                  
  done clear
  B)
          \[-\frac{x}{y}\]
  done clear
  C)
   \[\frac{y}{x}\]                  
  done clear
  D)
          \[-\frac{y}{x}\]
  done clear
  E)
   none of these
  done clear
  View Answer play_arrow

• question_answer207) The maximum value of\[\frac{\log x}{x}\]is equal to:
  A)
   \[\frac{2}{e}\]                 
  done clear
  B)
          \[\frac{1}{e}\]
  done clear
  C)
   \[e\]                    
  done clear
  D)
          \[1\]
  done clear
  E)
   \[\frac{e}{2}\]
  done clear
  View Answer play_arrow

• question_answer208) \[ax+by-{{a}^{2}}=0,\]where a, b are non-zero, is the equation to the straight line perpendicular to a line \[l\]and passing through the point where (crosses the\[x-\]axis. Then equation to the line\[l\]is:
  A)
   \[\frac{x}{b}-\frac{y}{a}=1\]                      
  done clear
  B)
   \[\frac{x}{a}-\frac{y}{b}=1\]
  done clear
  C)
   \[\frac{x}{b}+\frac{y}{a}=ab\]  
  done clear
  D)
          \[\frac{x}{a}-\frac{y}{b}=ab\]
  done clear
  E)
   \[\frac{x}{a}+\frac{y}{b}=ab\]
  done clear
  View Answer play_arrow

• question_answer209) \[\int{\frac{{{a}^{x/2}}}{\sqrt{{{a}^{-x}}-{{a}^{x}}}}}dx\]is equal to:
  A)
   \[\frac{1}{\log a}{{\sin }^{-1}}({{a}^{x}})+c\]
  done clear
  B)
   \[\frac{1}{\log a}{{\tan }^{-1}}({{a}^{x}})+c\]
  done clear
  C)
   \[2\sqrt{{{a}^{-x}}-{{a}^{x}}}+c\]
  done clear
  D)
   \[\log ({{a}^{x}}-1)+c\]
  done clear
  E)
   \[{{\sin }^{-1}}({{a}^{x}})+c\]
  done clear
  View Answer play_arrow

• question_answer210) If\[g(x)=\frac{f(x)-f(-x)}{2}\]defined over\[[-3,\text{ }3]\] and\[f(x)=2{{x}^{2}}-4x+1,\]then\[\int_{-3}^{3}{g(x)}dx\]is equal to:
  A)
   0                                            
  done clear
  B)
   4
  done clear
  C)
   \[-4\]                   
  done clear
  D)
          8
  done clear
  E)
   none of these
  done clear
  View Answer play_arrow

• question_answer211) Let ABCD be the parallelogram whose sides AB and AD are represented by the vectors \[2\hat{i}+4\hat{j}-5\hat{k}\]and\[\hat{i}+2\hat{j}+3\hat{k}\] respectively. Then, if a is a unit vector parallel to AC then a equals:
  A)
   \[\frac{1}{3}(3\hat{i}-6\hat{j}-2\hat{k})\]
  done clear
  B)
   \[\frac{1}{3}(3\hat{i}+6\hat{j}+2\hat{k})\]
  done clear
  C)
   \[\frac{1}{3}(3\hat{i}-6\hat{j}-3\hat{k})\]
  done clear
  D)
   \[\frac{1}{7}(3\hat{i}+6\hat{j}-2\hat{k})\]
  done clear
  E)
   \[\frac{1}{7}(3\hat{i}+5\hat{j}-3\hat{k})\]
  done clear
  View Answer play_arrow

• question_answer212) The solution of\[\frac{dy}{dx}+1=\cos ec(x+y)\]is:
  A)
   \[\cos (x+y)+x=c\]
  done clear
  B)
   \[\cos (x+y)=c\]
  done clear
  C)
   \[\sin (x+y)+x=c\]
  done clear
  D)
   \[\sin (x+y)+\sin (x+y)=c\]
  done clear
  E)
   \[x-\cos (x+y)=c\]
  done clear
  View Answer play_arrow

• question_answer213) Two finite sets have m and n elements. The number of elements in the power set of first set is 48 more than the total number of elements in the power set of the second set. Then the values of m and n are:
  A)
   \[7,6\]                 
  done clear
  B)
          \[6,3\]
  done clear
  C)
   \[6,4\]                 
  done clear
  D)
          \[7,4\]
  done clear
  E)
   \[3,7\]
  done clear
  View Answer play_arrow

• question_answer214) Let\[\overrightarrow{a}\]and\[\overrightarrow{b}\]be two unit vectors such that angle between them is\[60{}^\circ \]. Then\[|\overrightarrow{a}-\overrightarrow{b}|\]is equal to:
  A)
   \[\sqrt{5}\]                                       
  done clear
  B)
   \[\sqrt{3}\]
  done clear
  C)
   \[0\]                                    
  done clear
  D)
   \[1\]
  done clear
  E)
   \[\sqrt{2}\]
  done clear
  View Answer play_arrow

• question_answer215) Two numbers within the brackets denote the ranks of 10 students of a class in two subjects\[(1,10),(2,9),(3,8),(4,7),(5,6),(6,5)(7,4),(8,3)\]\[(9,2),(10,1),\]then rank correlation coefficient is:
  A)
   \[0\]                    
  done clear
  B)
          \[-1\]
  done clear
  C)
   \[1\]                    
  done clear
  D)
          \[0.5\]
  done clear
  E)
   \[-0.5\]
  done clear
  View Answer play_arrow

• question_answer216) \[\int{\frac{\sin x}{\sin (x-a)}}dx\]is equal to:
  A)
   \[x\cos a-\sin a.\log (x-a)+c\]
  done clear
  B)
   \[x\sin a+c\]
  done clear
  C)
   \[x\sin a+\sin a.\log \sin (x-a)+c\]
  done clear
  D)
   \[x\cos a+\sin a.\log \sin (x-a)+c\]
  done clear
  E)
   \[x\cos a+\cos a.\log \sin (x-a)+c\]
  done clear
  View Answer play_arrow

• question_answer217) If\[a=\hat{i}+2\hat{j}+3\hat{k},\]and \[\overrightarrow{b}=\hat{i}\times (\overrightarrow{a}\times \hat{i})+\hat{j}\times (\overrightarrow{a}\times \hat{j})+\overrightarrow{k}\times (\overrightarrow{a}\times \hat{k}),\] then length of \[\vec{b}\] is equal to
  A)
   \[\sqrt{12}\]     
  done clear
  B)
          \[2\sqrt{12}\]
  done clear
  C)
   \[3\sqrt{14}\]  
  done clear
  D)
          \[3\sqrt{12}\]
  done clear
  E)
                                  \[2\sqrt{14}\]
  done clear
  View Answer play_arrow

• question_answer218) \[\int{\frac{f(x)}{f(x)\log [f(x)]}}dx\]is equal to:
  A)
   \[\frac{f(x)}{\log f(x)}+c\]
  done clear
  B)
   \[f(x).\log f(x)+c\]
  done clear
  C)
   \[\log [\log f(x)]+c\]
  done clear
  D)
   \[\frac{1}{\log [\log f(x)]}+c\]
  done clear
  E)
   \[\frac{\log f(x)}{f(x)}+c\]
  done clear
  View Answer play_arrow

• question_answer219) \[\int{\frac{{{e}^{x}}}{(2+{{e}^{x}})({{e}^{x}}+1)}}dx\]is equal to:
  A)
   \[\log \left( \frac{{{e}^{x}}+1}{{{e}^{x}}+2} \right)+c\]  
  done clear
  B)
   \[\log \left( \frac{{{e}^{x}}+2}{{{e}^{x}}+1} \right)+c\]
  done clear
  C)
   \[\left( \frac{{{e}^{x}}+1}{{{e}^{x}}+2} \right)+c\]           
  done clear
  D)
          \[\left( \frac{{{e}^{x}}+2}{{{e}^{x}}+1} \right)+c\]
  done clear
  E)
   \[\frac{1}{2}\log \left( \frac{{{e}^{x}}+1}{{{e}^{x}}+2} \right)+c\]
  done clear
  View Answer play_arrow

• question_answer220) For any angle\[\theta ,\]the expression\[\frac{2\cos 8\theta +1}{2\cos \theta +1}\]is equal to:
  A)
   \[(2\cos \theta +1)(2\cos 2\theta +1)(2\cos 4\theta +1)\]
  done clear
  B)
   \[(\cos \theta -1)(\cos 2\theta -1)(\cos 4\theta -1)\]
  done clear
  C)
   \[(2\cos \theta -1)(2\cos 2\theta -1)(2\cos 4\theta -1)\]
  done clear
  D)
   \[(2\cos \theta +1)(2\cos 2\theta +1)(2\cos 4\theta +1)\]
  done clear
  E)
   \[(2\cos \theta -1)(2\cos 2\theta -1)(2\cos 4\theta +1)\]
  done clear
  View Answer play_arrow

• question_answer221) If\[{{I}_{n}}=\int_{0}^{\pi /4}{{{\tan }^{n}}\theta d\theta ,}\]then\[{{I}_{8}}+{{I}_{6}}\]is equal to:
  A)
   \[\frac{1}{7}\]  
  done clear
  B)
   \[\frac{1}{4}\]
  done clear
  C)
   \[\frac{1}{5}\]                  
  done clear
  D)
          \[\frac{1}{6}\]
  done clear
  E)
   \[\frac{1}{2}\]
  done clear
  View Answer play_arrow

• question_answer222) The order of the differential equation \[{{\left( \frac{{{d}^{2}}y}{d{{x}^{2}}} \right)}^{3}}={{\left( 1+\frac{dy}{dx} \right)}^{1/2}}\]is:
  A)
   2                            
  done clear
  B)
          3
  done clear
  C)
   \[\frac{1}{2}\]                  
  done clear
  D)
          4
  done clear
  E)
   6
  done clear
  View Answer play_arrow

• question_answer223) If\[m\tan (\theta -30{}^\circ )=n\tan (\theta +120{}^\circ ),\]then\[\cos 2\theta \]equals:
  A)
   \[\frac{m+n}{m-n}\]     
  done clear
  B)
          \[\frac{m-n}{m+n}\]
  done clear
  C)
   \[\frac{m-n}{2(m+n)}\]               
  done clear
  D)
          \[\frac{m+n}{2(m-n)}\]
  done clear
  E)
   \[\frac{2(m+n)}{m-n}\]
  done clear
  View Answer play_arrow

• question_answer224) The integrating factor of the differential equation\[\cos x\left( \frac{dy}{dx} \right)+y\sin x=1\]is:
  A)
   \[cos\text{ }x\]               
  done clear
  B)
          \[tan\text{ }x\]
  done clear
  C)
   \[sin\text{ }x\]                
  done clear
  D)
          \[cot\text{ }x\]
  done clear
  E)
   \[sec\text{ }x\]
  done clear
  View Answer play_arrow

• question_answer225) Solution of the differential equation \[\tan y.{{\sec }^{2}}xdx+\tan x.{{\sec }^{2}}ydy=0\] is:
  A)
   \[tan\text{ }x+tan\text{ }y=k\]
  done clear
  B)
   \[tan\text{ }x-tan\text{ }y=k\]
  done clear
  C)
   \[(tan\text{ }x/tan\text{ }y)=k\]
  done clear
  D)
   \[tan\text{ }x.tan\text{ }y=k\]
  done clear
  E)
   None of the above
  done clear
  View Answer play_arrow

• question_answer226) \[{{\tan }^{-1}}\left( \frac{m}{2} \right)-{{\tan }^{-1}}\left( \frac{m-n}{m+n} \right)\] is equal to:
  A)
   \[\frac{\pi }{4}\]                             
  done clear
  B)
          \[\frac{\pi }{2}\]
  done clear
  C)
   \[\frac{\pi }{3}\]                             
  done clear
  D)
          \[\frac{\pi }{8}\]
  done clear
  E)
   \[\frac{2\pi }{3}\]           
  done clear
  View Answer play_arrow

• question_answer227) A class has 175 students. The following data shows the number of students opting one or more subjects. Mathematics 100; Physics 70; Chemistry 40; Mathematics and Physics 30; Mathematics and Chemistry 28; Physics and Chemistry 23; Mathematics, Physics and Chemistry 18. How many students have offered Mathematics alone?
  A)
   35                         
  done clear
  B)
          48
  done clear
  C)
   60  
  done clear
  D)
          22
  done clear
  E)
   30
  done clear
  View Answer play_arrow

• question_answer228) Let S be the set of all real numbers. Then the relation\[R=\{(a,b):1+ab>0\}\]on S is:
  A)
   reflexive and symmetric but not transitive
  done clear
  B)
   reflexive and transitive but not symmetric
  done clear
  C)
   symmetric and transitive but not reflexive
  done clear
  D)
   reflexive, transitive and symmetric
  done clear
  E)
   none of the above is true
  done clear
  View Answer play_arrow

• question_answer229) For the principal value branch of the graph of the function\[y={{\sin }^{-1}}x,-1\le x\le 1,\]which among the following is a true statement?
  A)
   graph is symmetric about the\[x-\]axis
  done clear
  B)
   graph is symmetric about the y-axis
  done clear
  C)
   graph is not continuous
  done clear
  D)
   the line\[x=1\]is a tangent
  done clear
  E)
   the line y = 1 is a tangent
  done clear
  View Answer play_arrow

• question_answer230) Let\[f\left( x+\frac{1}{x} \right)={{x}^{2}}+\frac{1}{{{x}^{2}}},x\ne 0,\]then\[f(x)\] equals to:
  A)
   \[{{x}^{2}}\]                     
  done clear
  B)
          \[{{x}^{2}}-1\]
  done clear
  C)
   \[{{x}^{2}}-2\]                 
  done clear
  D)
          \[{{x}^{2}}+1\]
  done clear
  E)
   \[{{x}^{2}}+2\]
  done clear
  View Answer play_arrow

• question_answer231) A point P which represents a complex number z moves such that\[|z-{{z}_{1}}|=|z-{{z}_{2}}|,\]then its locus is:
  A)
   a circle with centre\[{{z}_{1}}\]
  done clear
  B)
   a circle with centre\[{{z}_{2}}\]
  done clear
  C)
   a circle with centre\[z\]
  done clear
  D)
   an ellipse
  done clear
  E)
   perpendicular bisector of line joining\[{{z}_{1}}\] and\[{{z}_{2}}\]
  done clear
  View Answer play_arrow

• question_answer232) The probability that in a family of 5 members, exactly 2 members have birthday on Sunday, is:
  A)
   \[\frac{12\times {{5}^{3}}}{{{7}^{5}}}\] 
  done clear
  B)
          \[\frac{10\times {{6}^{2}}}{{{7}^{5}}}\]
  done clear
  C)
   \[\frac{2}{5}\]                  
  done clear
  D)
          \[\frac{10\times {{6}^{3}}}{{{7}^{5}}}\]
  done clear
  E)
   \[1\]
  done clear
  View Answer play_arrow

• question_answer233) \[\frac{{{(\cos \theta +i\sin \theta )}^{4}}}{{{(\sin \theta +i\cos \theta )}^{5}}}\]is equal to:
  A)
   \[\cos \theta -i\sin \theta \]
  done clear
  B)
          \[\sin \theta -i\cos \theta \]
  done clear
  C)
   \[\cos 9\theta -i\sin 9\theta \]
  done clear
  D)
          \[\sin 9\theta -i\cos 9\theta \]
  done clear
  E)
   \[\cos \theta +i\sin \theta \]
  done clear
  View Answer play_arrow

• question_answer234) The quadratic equation whose roots are twice the roots of\[2{{x}^{2}}-5x+2=0\]is:
  A)
   \[8{{x}^{2}}-10x+2=0\]
  done clear
  B)
   \[{{x}^{2}}-5x+4=0\]
  done clear
  C)
   \[2{{x}^{2}}-5x+2=0\]
  done clear
  D)
   \[{{x}^{2}}-10x+6=0\]
  done clear
  E)
   none of the above
  done clear
  View Answer play_arrow

• question_answer235) Standard deviation of the first\[2n+1\]natural numbers is equal to:
  A)
   \[\sqrt{\frac{n(n+1)}{2}}\]         
  done clear
  B)
          \[\sqrt{\frac{n(n+1)(2n+1)}{3}}\]
  done clear
  C)
   \[\sqrt{\frac{n(n+1)}{3}}\]         
  done clear
  D)
          \[\sqrt{\frac{n(n-1)}{2}}\]
  done clear
  E)
   \[2n+1\]
  done clear
  View Answer play_arrow

• question_answer236) If\[\alpha +\beta =4\]and\[{{\alpha }^{3}}+{{\beta }^{3}}=44,\]then\[\alpha ,\beta \]are the roots of the equation.
  A)
   \[2{{x}^{2}}-7x+6=0\]
  done clear
  B)
   \[3{{x}^{2}}+9x+11=0\]
  done clear
  C)
  \[9{{x}^{2}}-27x+20=0\]
  done clear
  D)
   \[4{{x}^{2}}+22x+15=0\]
  done clear
  E)
   \[3{{x}^{2}}-12x-5=0\]
  done clear
  View Answer play_arrow

• question_answer237) The coefficient of\[x\]in\[{{x}^{2}}+px+q=0\]was taken as 17 in place of 13 and its roots were found to be\[-2\]and\[-15\]The roots of the original equation are:
  A)
   3, 7                       
  done clear
  B)
          \[-3,7\]
  done clear
  C)
   \[-3,-7\]             
  done clear
  D)
          \[3,10\]
  done clear
  E)
   \[-3,-10\]
  done clear
  View Answer play_arrow

• question_answer238) If\[g(x)=\min (x,{{x}^{2}})\]where\[x\]is a real number, then:
  A)
  \[g(x)\]is an increasing function
  done clear
  B)
  \[g(x)\]is a decreasing function
  done clear
  C)
   \[g(x)\] is a constant function
  done clear
  D)
  \[g(x)\]is a continuous function except at\[x=0\]
  done clear
  E)
  \[g(x)\]is a continuous function except at \[x=0\]and\[x=1\]
  done clear
  View Answer play_arrow

• question_answer239) If\[^{n}{{C}_{3}}=220,\]then n equals to:
  A)
   10                         
  done clear
  B)
          11
  done clear
  C)
   12                         
  done clear
  D)
          9
  done clear
  E)
   8
  done clear
  View Answer play_arrow

• question_answer240) A polygon has 54 diagonals. Number of sides of this polygon is:
  A)
   12                         
  done clear
  B)
          15
  done clear
  C)
   16                         
  done clear
  D)
          9
  done clear
  E)
   14
  done clear
  View Answer play_arrow