question_answer 1) A straight conductor carries a current of 5 A. An electron travelling with a speed of \[5\times {{10}^{6}}m{{s}^{-1}}\]parallel to the wire at a distance of 0.1 m from the conductor, experiences a force of:
A)
\[8\times {{10}^{-20}}N\]
done
clear
B)
\[3.2\times {{10}^{-19}}N\]
done
clear
C)
\[8\times {{10}^{-18}}N\]
done
clear
D)
\[1.6\times {{10}^{-19}}N\]
done
clear
E)
zero
done
clear
View Answer play_arrow
question_answer 2) Two galvanometers A and B require currents of 3 mA and 5 mA respectively to produce the same deflection of 10 divisions. Then:
A)
A is more sensitive than B
done
clear
B)
B is more sensitive than A
done
clear
C)
A and B are equally sensitive
done
clear
D)
sensitiveness of B is twice that of A
done
clear
E)
sensitiveness of B is 5/3 times that of A
done
clear
View Answer play_arrow
question_answer 3) The temperature of an ideal gas is reduced from\[927{}^\circ C\]to\[27{}^\circ C\]The rms velocity of the molecules becomes:
A)
double the initial value
done
clear
B)
half of the initial value
done
clear
C)
four times the initial value
done
clear
D)
ten times the initial value
done
clear
E)
\[\sqrt{(927/27)}\]
done
clear
View Answer play_arrow
question_answer 4) The pressure at the bottom of a tank containing a liquid does not depend on:
A)
acceleration due to gravity
done
clear
B)
height of the liquid column
done
clear
C)
area of the bottom surface
done
clear
D)
density of the liquid
done
clear
E)
nature of the liquid
done
clear
View Answer play_arrow
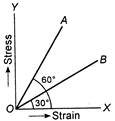
question_answer 5)
The stress versus strain graphs for wires of two materials A and B are as shown in the figure. If\[{{Y}_{A}}\]and\[{{Y}_{B}}\]are the Youngs modulus of the materials, then:
A)
\[{{Y}_{B}}=2{{Y}_{A}}\]
done
clear
B)
\[{{Y}_{A}}={{Y}_{B}}\]
done
clear
C)
\[{{Y}_{B}}=3{{Y}_{A}}\]
done
clear
D)
\[{{Y}_{A}}=3{{Y}_{B}}\]
done
clear
E)
\[{{Y}_{B}}=\frac{1}{3}{{Y}_{A}}\]
done
clear
View Answer play_arrow
question_answer 6) Two vectors\[\overrightarrow{A}\]and \[\overrightarrow{B}\]are such that \[|\overrightarrow{A}\times \overrightarrow{B}|=|\overrightarrow{A}.\overrightarrow{B}|\]then the angle between the two vectors is:
A)
\[60{}^\circ \]
done
clear
B)
\[90{}^\circ \]
done
clear
C)
\[0{}^\circ \]
done
clear
D)
\[45{}^\circ \]
done
clear
E)
\[30{}^\circ \]
done
clear
View Answer play_arrow
question_answer 7) A truck of mass 30000 kg moves up an inclined plane of slope 1 in 100 at speed of 30 km/h. The power of the truck is (given \[g=10\text{ }m{{s}^{-1}}\]):
A)
25 kW
done
clear
B)
10 kW
done
clear
C)
5 kW
done
clear
D)
2.5 kW
done
clear
E)
0.5 kW
done
clear
View Answer play_arrow
question_answer 8) A circular thin disc of mass 2 kg has a diameter 0.2 m. Calculate its moment of inertia about an axis passing through the edge and perpendicular to the plane of the disc (in\[kg-{{m}^{2}}\]):
A)
0.01
done
clear
B)
0.03
done
clear
C)
0.02
done
clear
D)
3
done
clear
E)
2
done
clear
View Answer play_arrow
question_answer 9) A torque of 50 Nm acting on a wheel at rest rotates it through 200 rad in 5 s. Calculate the angular acceleration produced.
A)
\[8\text{ }rad\text{ }{{s}^{-2}}\]
done
clear
B)
\[4\text{ }rad\text{ }{{s}^{-2}}\]
done
clear
C)
\[\text{16 }rad\text{ }{{s}^{-2}}\]
done
clear
D)
\[\text{12 }rad\text{ }{{s}^{-2}}\]
done
clear
E)
\[\text{10 }rad\text{ }{{s}^{-2}}\]
done
clear
View Answer play_arrow
question_answer 10) The distance between the carbon atom and the oxygen atom in a carbon monoxide molecule is \[1.1\overset{\text{o}}{\mathop{\text{A}}}\,\]. Given, mass of carbon atom is 12 amu and mass of oxygen atom is 16 amu. Calculate the position of the centre of mass of the carbon monoxide molecule:
A)
\[6.3\overset{\text{o}}{\mathop{\text{A}}}\,\] from the carbon atom
done
clear
B)
\[1\overset{\text{o}}{\mathop{\text{A}}}\,\] from the oxygen atom
done
clear
C)
\[0.63\overset{\text{o}}{\mathop{\text{A}}}\,\] from the carbon atom
done
clear
D)
\[0.12\overset{\text{o}}{\mathop{\text{A}}}\,\] from the oxygen atom
done
clear
E)
\[0.16\overset{\text{o}}{\mathop{\text{A}}}\,\] from the carbon atom
done
clear
View Answer play_arrow
question_answer 11) A cyclist riding the bicycle at a speed of \[14\sqrt{3}\text{ }m{{s}^{-1}}\]takes a turn around a circular road of radius\[20\sqrt{3}\]m without skidding. Given, \[g=9.8\text{ }m{{s}^{-2}},\]what is his inclination to the vertical?
A)
\[30{}^\circ \]
done
clear
B)
\[90{}^\circ \]
done
clear
C)
\[45{}^\circ \]
done
clear
D)
\[60{}^\circ \]
done
clear
E)
\[0{}^\circ \]
done
clear
View Answer play_arrow
question_answer 12) Masses of stars and galaxies are usually expressed in terms of:
A)
neutron mass
done
clear
B)
earths mass
done
clear
C)
nuclear mass
done
clear
D)
proton mass
done
clear
E)
solar mass
done
clear
View Answer play_arrow
question_answer 13) Relation between the colour and the temperature of a star is given by:
A)
Weins displacement law
done
clear
B)
Plancks law
done
clear
C)
Hubble slaw
done
clear
D)
Hippacrus law
done
clear
E)
Fraunhoffer diffraction law
done
clear
View Answer play_arrow
question_answer 14) 27 identical drops of water are falling down vertically in air each with a terminal velocity\[0.15\text{ }m{{s}^{-1}}\]. If they combine to form a single bigger drop, what will be its terminal velocity?
A)
\[0.3\text{ }m{{s}^{-1}}\]
done
clear
B)
\[1.35\,m{{s}^{-1}}\]
done
clear
C)
\[0.45\,m{{s}^{-1}}\]
done
clear
D)
zero
done
clear
E)
\[0.95\,m{{s}^{-1}}\]
done
clear
View Answer play_arrow
question_answer 15) 25 tuning forks are arranged in series in the order of decreasing frequency. Any two successive forks produce 3 beats/s. If the frequency of the first tuning fork is the octave of the last fork, then the frequency of the 21st fork is:
A)
72 Hz
done
clear
B)
288 Hz
done
clear
C)
84 Hz
done
clear
D)
87 Hz
done
clear
E)
144 Hz
done
clear
View Answer play_arrow
question_answer 16) A spherical conductor of radius 2 m is charged to a potential of 120 V. It is now placed inside another hollow spherical conductor of radius 6 m. Calculate the potential to which the bigger sphere would be raised, if the smaller sphere is made to touch the bigger sphere.
A)
20 V
done
clear
B)
60 V
done
clear
C)
80 V
done
clear
D)
40 V
done
clear
E)
120V
done
clear
View Answer play_arrow
question_answer 17)
Velocity of sound in air: (I) increases with temperature (II) decreases with temperature (III) increases with pressure (IV) is independent of pressure (V) decreases with pressure (VI) is independent of temperature
Choose the correct answer:
A)
Only I and II are true
done
clear
B)
Only I and III are true
done
clear
C)
Only I and V are true
done
clear
D)
Only II and III are true
done
clear
E)
Only I and IV are true
done
clear
View Answer play_arrow
question_answer 18) A capacitor is used to store 24 Wh of energy at 1200 V. What should be the capacitance of the capacitor?
A)
\[120\,mF\]
done
clear
B)
\[120\,\mu F\]
done
clear
C)
\[24\,\mu F\]
done
clear
D)
\[24\,mF\]
done
clear
E)
\[12\,\mu F\]
done
clear
View Answer play_arrow
question_answer 19) A uniform wire of resistance\[9\,\Omega \]is cut into equal parts. They are connected in the form of equilateral triangle ABC. A cell of emf 2 V and negligible internal resistance is connected across B and C. Potential difference across AB is:
A)
1 V
done
clear
B)
2 V
done
clear
C)
3 V
done
clear
D)
0.5 V
done
clear
E)
0.25 V
done
clear
View Answer play_arrow
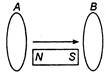
question_answer 20)
In the diagram shown if a bar magnet is moved along the common axis of two single turn coils A and B in the direction of arrow:
A)
current is induced only in A and not in B
done
clear
B)
induced currents in A and B are in the same direction
done
clear
C)
current is induced only in B and not in A
done
clear
D)
no current is induced in either A or B
done
clear
E)
induced currents in A and B are in opposite directions
done
clear
View Answer play_arrow
question_answer 21) In a potentiometer experiment two cells of emf\[{{E}_{1}}\]and\[{{E}_{2}}\]are used in series and in conjunction and the balancing length is found to be 58 cm of the wire. If the polarity of\[{{E}_{2}}\]is reversed, then the balancing length becomes 29 cm. The ratio\[{{E}_{1}}/{{E}_{2}}\]of the emfs of the two cells is:
A)
\[1:1\]
done
clear
B)
\[2:1\]
done
clear
C)
\[3:1\]
done
clear
D)
\[4:1\]
done
clear
E)
\[1:2\]
done
clear
View Answer play_arrow
question_answer 22) A block of mass 10 kg is placed on an inclined plane. When the angle of inclination is\[30{}^\circ ,\] the block just begins to slide down the plane. The force of static friction is:
A)
10 kg-wt
done
clear
B)
9.8 kg-wt
done
clear
C)
49 kg-wt
done
clear
D)
5 kg-wt
done
clear
E)
15 kg-wt
done
clear
View Answer play_arrow
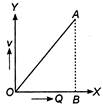
question_answer 23)
Charge Q on a capacitor varies with voltage V as shown in the figure, where Q is taken along the X-axis and V along the V-axis. The area of triangle OAB represents:
A)
capacitance
done
clear
B)
capacitive reactance
done
clear
C)
magnetic field between the plates
done
clear
D)
electric flux between the plates
done
clear
E)
energy stored in the capacitor
done
clear
View Answer play_arrow
question_answer 24) Consider two point charges of equal magnitude and opposite sign separated by certain distance. The neutral point due to them:
A)
does not exist
done
clear
B)
will be in midway between them
done
clear
C)
lies on the perpendicular bisector of line joining the two
done
clear
D)
will be outside on the line joining them
done
clear
E)
will be closer to the negative charge
done
clear
View Answer play_arrow
question_answer 25) Calculate the amount of charge flowing in min in a wire of resistance 100, when a potential difference of 20 V is applied between its ends.
A)
120 C
done
clear
B)
240 C
done
clear
C)
20 C
done
clear
D)
4 C
done
clear
E)
80 C
done
clear
View Answer play_arrow
question_answer 26) The SI unit of electric flux is:
A)
\[Wb\]
done
clear
B)
\[N/C\]
done
clear
C)
\[V-m\]
done
clear
D)
\[J/C\]
done
clear
E)
none of these
done
clear
View Answer play_arrow
question_answer 27) A radioactive nucleus emits beta particle. The parent and daughter nuclei are:
A)
isotopes
done
clear
B)
isotones
done
clear
C)
isomers
done
clear
D)
isobars
done
clear
E)
isothermals
done
clear
View Answer play_arrow
question_answer 28) \[{{\mu }_{0}}\]denotes absolute permeability and \[{{E}_{0}}\]denotes the absolute permittivity of free space. Then the velocity of electromagnetic waves in free space is:
A)
\[{{\mu }_{0}}{{\varepsilon }_{0}}\]
done
clear
B)
\[\sqrt{{{\mu }_{0}}/{{\varepsilon }_{0}}}\]
done
clear
C)
\[\sqrt{{{\mu }_{0}}{{\varepsilon }_{0}}}\]
done
clear
D)
\[{{\varepsilon }_{0}}/{{\mu }_{0}}\]
done
clear
E)
\[1/\sqrt{{{\mu }_{0}}/{{\varepsilon }_{0}}}\]
done
clear
View Answer play_arrow
question_answer 29) The unit of focal power of a lens is:
A)
watt
done
clear
B)
horse power
done
clear
C)
diopter
done
clear
D)
lux
done
clear
E)
candela
done
clear
View Answer play_arrow
question_answer 30) An underwater swimmer is at a depth of 12 m below the surface of water. A bird is at a height of 18 m from the surface of water, directly above his eyes. For the swimmer the bird appears to be at a distance of .....from the surface of water. (Refractive index of water is 4/3):
A)
24 m
done
clear
B)
12 m
done
clear
C)
18 m
done
clear
D)
9 m
done
clear
E)
16m
done
clear
View Answer play_arrow
question_answer 31) If the red light is replaced by blue light illuminating the object in a microscope the resolving power of the microscope:
A)
decreases
done
clear
B)
increases
done
clear
C)
gets halved
done
clear
D)
remains unchanged
done
clear
E)
becomes 1/4 of the original value
done
clear
View Answer play_arrow
question_answer 32) Five identical lamps grouped together produce a certain illumination on a screen kept 5 m from the lamps. If three of the lamps are switched off, through what distance should the group of lamps be moved to obtain the same illumination on the screen? (Assume normal incidence)
A)
\[\sqrt{10}m\]towards the screen
done
clear
B)
\[(5+\sqrt{10})m\]towards the screen
done
clear
C)
\[(5-\sqrt{10})m\]towards the screen
done
clear
D)
\[(5-\sqrt{10})m\]away from the screen
done
clear
E)
\[\sqrt{10}\]away from the screen
done
clear
View Answer play_arrow
question_answer 33) For a thermocouple the neutral temperature is\[270{}^\circ C\]when its cold junction is at\[20{}^\circ C\]. What will be the neutral temperature and the temperature of inversion when the temperature of cold junction is increased to\[40{}^\circ C\]?
A)
\[290{}^\circ C,580{}^\circ C\]
done
clear
B)
\[270{}^\circ C,580{}^\circ C\]
done
clear
C)
\[270{}^\circ C,500{}^\circ C\]
done
clear
D)
\[290{}^\circ C,540{}^\circ C\]
done
clear
E)
\[290{}^\circ C,500{}^\circ C\]
done
clear
View Answer play_arrow
question_answer 34) The amount of heat produced in a resistor when a current is passed through it, can be found using:
A)
Faradays law
done
clear
B)
Kirchhoffs law
done
clear
C)
Laplaces law
done
clear
D)
Joules law
done
clear
E)
Lenzs law
done
clear
View Answer play_arrow
question_answer 35) A body cools in 7 min from\[60{}^\circ C\]to\[40{}^\circ C\]. What time (in min) does it take to cool from \[40{}^\circ C\]to\[28{}^\circ C,\]if surrounding temperature is\[10{}^\circ C\]? (Assume Newtons law of cooling)
A)
3.5
done
clear
B)
14
done
clear
C)
7
done
clear
D)
10
done
clear
E)
21
done
clear
View Answer play_arrow
question_answer 36) In a Carnot heat engine 8000 J of heat is absorbed from a source at 400 K and 6400 J of heat is rejected to the sink. The temperature of the sink is:
A)
320 K
done
clear
B)
100 K
done
clear
C)
zero
done
clear
D)
273 K
done
clear
E)
400 K
done
clear
View Answer play_arrow
question_answer 37) Heat is flowing through two cylindrical rods A and B of same material having the same temperature difference between their ends. The diameters of rods A and B are in the ratio 1 : 2 and their lengths in the ratio 2:1. The ratio of the rate of flow of heat in rod A to that in rod B is:
A)
\[2:1\]
done
clear
B)
\[2:3\]
done
clear
C)
\[1:1\]
done
clear
D)
\[1:8\]
done
clear
E)
4: 1
done
clear
View Answer play_arrow
question_answer 38) Identify, the pair which has different dimensions:
A)
Plancks constant and angular momentum
done
clear
B)
impulse and linear momentum
done
clear
C)
angular momentum and frequency
done
clear
D)
pressure and Youngs modulus
done
clear
E)
angular velocity and frequency
done
clear
View Answer play_arrow
question_answer 39) The dimensional formula\[[{{M}^{0}}{{L}^{2}}{{T}^{-2}}]\]stands for:
A)
torque
done
clear
B)
angular momentum
done
clear
C)
latent heat
done
clear
D)
coefficient for thermal conductivity
done
clear
E)
electrical potential
done
clear
View Answer play_arrow
question_answer 40) A particle moves along a semicircle of radius 10 m in 5 s. The velocity of the particle is:
A)
\[2\pi \,m{{s}^{-1}}\]
done
clear
B)
\[4\pi \,\,m{{s}^{-1}}\]
done
clear
C)
\[2\,m{{s}^{-1}}\]
done
clear
D)
\[4\,\,m{{s}^{-1}}\]
done
clear
E)
\[5\pi \,\,m{{s}^{-1}}\]
done
clear
View Answer play_arrow
question_answer 41) A body is thrown vertically upwards with a velocity u. Find the true statement from the following:
A)
Both velocity and acceleration are zero at its highest point
done
clear
B)
Velocity is maximum and acceleration is zero at the highest point
done
clear
C)
Velocity is maximum and acceleration is g downwards at its highest point
done
clear
D)
Velocity is zero at the highest point and maximum height reached is\[{{u}^{2}}/2g\]
done
clear
E)
Kinetic energy is maximum and velocity is zero at the highest point
done
clear
View Answer play_arrow
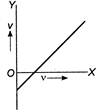
question_answer 42)
The stopping potential for photoelectric emission from a metal surface is plotted along Y-axis and frequency v of incident light along X-axis. A straight line is obtained as shown. Plancks constant is given by:
A)
slope of the line
done
clear
B)
product of slope of the line and charge on the electron
done
clear
C)
intercept along Y-axis divided by charge on the electron
done
clear
D)
product of intercept along X-axis and mass of the electron
done
clear
E)
product of slope and mass of the electron
done
clear
View Answer play_arrow
question_answer 43) A solid disc of mass M is just held in air horizontally by throwing 40 stones per second vertically upwards to strike the disc each with a velocity\[6\text{ }m{{s}^{-1}}\]. If the mass of each stone is 0.05 kg, what is the mass of the disc? \[(g=10\text{ }m{{s}^{-2}})\]
A)
1.2 kg
done
clear
B)
0.5 kg
done
clear
C)
20 kg
done
clear
D)
3 kg
done
clear
E)
4kg
done
clear
View Answer play_arrow
question_answer 44) A stone of mass m is tied to a string and is moved in a vertical circle of radius r making n rev/min. The total tension in the string when the stone is at its lowest point is:
A)
\[mg\]
done
clear
B)
\[m(g+\pi n{{r}^{2}})\]
done
clear
C)
\[m(g+nr)\]
done
clear
D)
\[m(g+{{n}^{2}}{{r}^{2}})\]
done
clear
E)
\[m\left\{ g+\frac{{{\pi }^{2}}{{n}^{2}}r}{900} \right\}\]
done
clear
View Answer play_arrow
question_answer 45) \[{{\lambda }_{a}}\]and\[{{\lambda }_{m}}\]are the wavelengths of a beam of light in air and medium respectively. If\[\theta \]is the polarizing angle, the correct relation between \[{{\lambda }_{a}}{{\lambda }_{m}}\]and\[\theta \]is:
A)
\[{{\lambda }_{a}}={{\lambda }_{m}}{{\tan }^{2}}\theta \]
done
clear
B)
\[{{\lambda }_{m}}={{\lambda }_{a}}{{\tan }^{2}}\theta \]
done
clear
C)
\[{{\lambda }_{a}}={{\lambda }_{m}}\cot \theta \]
done
clear
D)
\[{{\lambda }_{m}}={{\lambda }_{a}}\cot \theta \]
done
clear
E)
\[{{\lambda }_{m}}={{\lambda }_{a}}\sin \theta \]
done
clear
View Answer play_arrow
question_answer 46) A point P on the rim of a wheel is initially at rest and in contact with the ground. Find the displacement of the point P if the radius of the wheel is 5m and the wheel rolls forward through half a revolution:
A)
5 m
done
clear
B)
10 m
done
clear
C)
2.5m
done
clear
D)
\[5\left( \sqrt{2{{\pi }^{2}}+8} \right)\]
done
clear
E)
\[5\left( \sqrt{{{\pi }^{2}}+4} \right)\]
done
clear
View Answer play_arrow
question_answer 47) Water venturimeter works on the principle of:
A)
Newtons third law of motion
done
clear
B)
Strokes formula
done
clear
C)
Bernoullis theorem
done
clear
D)
Hookes law
done
clear
E)
Brewsters law
done
clear
View Answer play_arrow
question_answer 48) The total energy of a particle executing SHM is 80 J. What is the potential energy when the particle is at a distance of 3/4 of amplitude from the mean position?
A)
60 J
done
clear
B)
10 J
done
clear
C)
40 J
done
clear
D)
45 J
done
clear
E)
zero
done
clear
View Answer play_arrow
question_answer 49) The scale of a spring balance reading from 0 to 10 kg is 0.25 m long. A body suspended from the balance oscillates vertically with a period of\[\pi /10\,s\]s. The mass suspended is: (neglect the mass of the spring)
A)
10 kg
done
clear
B)
0.98 kg
done
clear
C)
5kg
done
clear
D)
20 kg
done
clear
E)
4kg
done
clear
View Answer play_arrow
question_answer 50) In a Youngs double slit experiment if the monochromatic source is replaced by a source of white light:
A)
fringes will be alternately white and black
done
clear
B)
central fringe is dark and other are coloured
done
clear
C)
central fringe is white and other are coloured
done
clear
D)
central fringe is coloured and all others are white
done
clear
E)
fringes vanish
done
clear
View Answer play_arrow
question_answer 51) A parallel beam of monochromatic light is incident normally on a slit. The diffraction pattern is observed on a screen placed at the focal plane of a convex lens. If the slit width is increased, the central maximum of the diffraction pattern will:
A)
become broader and fainter
done
clear
B)
become broader and brighter
done
clear
C)
become narrower and fainter
done
clear
D)
become narrower and brighter
done
clear
E)
remain unchanged
done
clear
View Answer play_arrow
question_answer 52) Assume that the acceleration due to gravity on the surface of the moon is 0.2 times the acceleration due to gravity on the surface of the earth. If\[{{R}_{e}}\]is the maximum range of a projectile on the earths surface, what is the maximum range on the surface of the moon for the same velocity of projection?
A)
\[0.2{{R}_{e}}\]
done
clear
B)
\[2{{R}_{e}}\]
done
clear
C)
\[0.5{{R}_{e}}\]
done
clear
D)
Zero
done
clear
E)
\[5{{R}_{e}}\]
done
clear
View Answer play_arrow
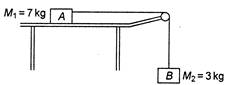
question_answer 53)
A block A of mass 7 kg is placed on a frictionless table. A thread tied to it passes over a frictionless pulley and carries a body B of mass kg at the other end. The acceleration of the system is: (given\[g=10\text{ }m{{s}^{-2}}\])
A)
\[100\,m{{s}^{-2}}\]
done
clear
B)
\[3\,m{{s}^{-2}}\]
done
clear
C)
\[10\,m{{s}^{-2}}\]
done
clear
D)
\[30\,\,m{{s}^{-2}}\]
done
clear
E)
zero
done
clear
View Answer play_arrow
question_answer 54) The orbital speed of an artificial satellite very close to the surface of the earth is\[{{v}_{o}}\]. Then the orbital speed of another artificial satellite at a height equal to the three times the radius of the earth is:
A)
\[4\,{{v}_{o}}\]
done
clear
B)
\[2\,{{v}_{o}}\]
done
clear
C)
\[0.5\,{{v}_{o}}\]
done
clear
D)
\[{{v}_{o}}\]
done
clear
E)
\[2/3\,{{v}_{o}}\]
done
clear
View Answer play_arrow
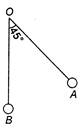
question_answer 55)
The bob A of a simple pendulum is released when the string makes an angle of\[{{45}^{o}}\] with the vertical. It hits an other bob B of the same material and same mass kept at rest on the table. If the collision is elastic:
A)
both A and B rise to the b same height
done
clear
B)
both A and B come to rest at B
done
clear
C)
both A and B move with the same velocity of A
done
clear
D)
A comes to rest and B moves with the velocity of A
done
clear
E)
B moves first and A follows it with half of its initial velocity
done
clear
View Answer play_arrow
question_answer 56) A body of mass 10 kg at rest is acted upon simultaneously by two forces 4 N and 3 N at right angles to each other. The kinetic energy of the body at the end of 10 s is:
A)
100 J
done
clear
B)
300 J
done
clear
C)
50 J
done
clear
D)
20 J
done
clear
E)
125J
done
clear
View Answer play_arrow
question_answer 57) A battery of emf 12 V and internal resistance \[2\,\Omega \]is connected in series with a tangent galvanometer of resistance\[4\,\Omega \]. The deflection is\[60{}^\circ \]when the plane of the coil is along the magnetic meridian. To get a deflection of\[30{}^\circ ,\]the resistance to be connected in series with the tangent galvanometer is:
A)
120
done
clear
B)
200
done
clear
C)
100
done
clear
D)
50
done
clear
E)
30
done
clear
View Answer play_arrow
question_answer 58) Identify the paramagnetic substance:
A)
iron
done
clear
B)
aluminium
done
clear
C)
nickel
done
clear
D)
hydrogen
done
clear
E)
copper
done
clear
View Answer play_arrow
question_answer 59) Which one of the following is not used to reduce friction?
A)
Oil
done
clear
B)
Ball bearing
done
clear
C)
Sand
done
clear
D)
Graphite
done
clear
E)
Compressed, purified air
done
clear
View Answer play_arrow
question_answer 60) If\[I\]is the moment of inertia and E is the kinetic energy of rotation of a body, then its angular momentum will be:
A)
\[\sqrt{(EI)}\]
done
clear
B)
\[2IE\]
done
clear
C)
\[E/I\]
done
clear
D)
\[\sqrt{(2EI)}\]
done
clear
E)
\[IE\]
done
clear
View Answer play_arrow
question_answer 61) Greenhouse effect is caused by:
A)
UV-rays
done
clear
B)
X-rays
done
clear
C)
gamma rays
done
clear
D)
cathode rays
done
clear
E)
infrared rays
done
clear
View Answer play_arrow
question_answer 62) If a\[{{H}_{2}}\]nucleus is completely converted into energy, the energy produced will be around:
A)
1 MeV
done
clear
B)
939 MeV
done
clear
C)
9.39 MeV
done
clear
D)
238 MeV
done
clear
E)
200 MeV
done
clear
View Answer play_arrow
question_answer 63) Radius of the first orbit of the electron in a hydrogen atom is \[0.53\overset{\text{o}}{\mathop{\text{A}}}\,\]. So, the radius of the third orbit will be:
A)
\[2.12\overset{\text{o}}{\mathop{\text{A}}}\,\]
done
clear
B)
\[4.77\overset{\text{o}}{\mathop{\text{A}}}\,\]
done
clear
C)
\[1.06\overset{\text{o}}{\mathop{\text{A}}}\,\]
done
clear
D)
\[1.59\overset{\text{o}}{\mathop{\text{A}}}\,\]
done
clear
E)
\[0.18\overset{\text{o}}{\mathop{\text{A}}}\,\]
done
clear
View Answer play_arrow
question_answer 64) Two inputs of NAND gate are shorted. This gate is equivalent to:
A)
OR gate
done
clear
B)
AND gate
done
clear
C)
NOT gate
done
clear
D)
XOR gate
done
clear
E)
NOR gate
done
clear
View Answer play_arrow
question_answer 65) A transistor is used in common-emitter configuration. Given its\[\alpha =0.9,\]calculate the change in collector current when the base current changes by\[2\,\mu A\].
A)
\[1\,\mu A\]
done
clear
B)
\[0.9\,\mu A\]
done
clear
C)
\[30\,\mu A\]
done
clear
D)
\[18\,\mu A\]
done
clear
E)
\[9\,\mu A\]
done
clear
View Answer play_arrow
question_answer 66) The thickness of the depletion layer in a p -n junction diode is of the order of:
A)
\[{{10}^{-3}}mm\]
done
clear
B)
\[{{10}^{-6}}mm\]
done
clear
C)
\[{{10}^{-3}}m\]
done
clear
D)
\[{{10}^{-8}}m\]
done
clear
E)
\[{{10}^{-4}}m\]
done
clear
View Answer play_arrow
question_answer 67) Which is not true with respect to the cathode rays?
A)
A stream of electrons
done
clear
B)
Charged particles
done
clear
C)
Move with speed as that of light
done
clear
D)
Can be deflected by magnetic fields
done
clear
E)
Can be deflected by electric fields
done
clear
View Answer play_arrow
question_answer 68) The kinetic energy of an electron accelerated from rest through a potential difference of 5 V will be:
A)
\[5J\]
done
clear
B)
\[5erg\]
done
clear
C)
\[5eV\]
done
clear
D)
\[8\times {{10}^{-19}}eV\]
done
clear
E)
\[80eV\]
done
clear
View Answer play_arrow
question_answer 69) Voltage and current in an AC circuit are given by\[V=5\sin \left( 100\pi t-\frac{\pi }{6} \right)\]and \[I=4\sin \left( 100\pi t+\frac{\pi }{6} \right)\]
A)
voltage leads the current by\[30{}^\circ \]
done
clear
B)
current leads the voltage by\[30{}^\circ \]
done
clear
C)
current leads the voltage by\[60{}^\circ \]
done
clear
D)
voltage leads the current by\[60{}^\circ \]
done
clear
E)
current and voltage are in phase
done
clear
View Answer play_arrow
question_answer 70) A bar magnet is released into a copper ring directly below it. The acceleration of the magnet will be:
A)
equal to the acceleration due to gravity at that place
done
clear
B)
less than the acceleration due to gravity at that place
done
clear
C)
greater than the acceleration due to gravity at that place
done
clear
D)
twice the acceleration due to gravity at that place
done
clear
E)
zero
done
clear
View Answer play_arrow
question_answer 71) Energy stored in a coil of self-inductance \[40\text{ }mH\]carrying a steady current of 2 A, is:
A)
8 J
done
clear
B)
0.8 J
done
clear
C)
0.08 J
done
clear
D)
80 J
done
clear
E)
4J
done
clear
View Answer play_arrow
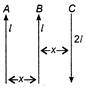
question_answer 72)
A, B and C are parallel conductors of equal lengths carrying currents\[I,I\]and\[2I\]respectively. Distance between A and B is X. Distance between B and C is also\[x\].\[{{F}_{1}}\]is the force exerted by B on A.\[{{F}_{2}}\]is the force exerted by C on A. Choose the correct answer:
A)
\[{{F}_{1}}=2{{F}_{2}}\]
done
clear
B)
\[{{F}_{2}}=2{{F}_{1}}\]
done
clear
C)
\[{{F}_{1}}={{F}_{2}}\]
done
clear
D)
\[{{F}_{1}}=-{{F}_{2}}\]
done
clear
E)
\[{{F}_{2}}=4{{F}_{1}}\]
done
clear
View Answer play_arrow
question_answer 73) When ethylene glycol is heated with acidified potassium permanganate, the main organic compound obtained is:
A)
oxalic acid
done
clear
B)
glyoxal
done
clear
C)
formic acid
done
clear
D)
acetaldehyde
done
clear
E)
2-hydroxy ethanol
done
clear
View Answer play_arrow
question_answer 74) \[C{{H}_{3}}C{{H}_{2}}C{{H}_{2}}OH\]and\[{{H}_{3}}CC{{H}_{2}}OC{{H}_{3}}\]are:
A)
position isomers
done
clear
B)
chain isomers
done
clear
C)
geometrical isomers
done
clear
D)
functional isomers
done
clear
E)
optical isomers
done
clear
View Answer play_arrow
question_answer 75) The atomicity of sulphur in rhombic sulphur is:
A)
1
done
clear
B)
2
done
clear
C)
4
done
clear
D)
6
done
clear
E)
8
done
clear
View Answer play_arrow
question_answer 76) The rate of diffusion of methane at a given temperature is twice of a gas X. The molar mass of the gas X is:
A)
64
done
clear
B)
32
done
clear
C)
16
done
clear
D)
8
done
clear
E)
4
done
clear
View Answer play_arrow
question_answer 77) The aqueous solution/liquid that absorbs nitric oxide to a considerable extent is:
A)
lead nitrate
done
clear
B)
nitric acid
done
clear
C)
ferrous sulphate
done
clear
D)
sodium hydroxide
done
clear
E)
carbon disulphide
done
clear
View Answer play_arrow
question_answer 78) The compound without a chiral carbon atom is:
A)
\[BrC{{H}_{2}}\overset{\begin{smallmatrix} C{{H}_{3}} \\ | \end{smallmatrix}}{\mathop{CH}}\,C{{H}_{2}}Br\]
done
clear
B)
\[{{C}_{2}}{{H}_{5}}C{{H}_{2}}\overset{\begin{smallmatrix} C{{H}_{3}} \\ | \end{smallmatrix}}{\mathop{CH}}\,C{{H}_{2}}Br\]
done
clear
C)
\[{{C}_{3}}{{H}_{2}}\underset{\begin{smallmatrix} | \\ C{{H}_{3}} \end{smallmatrix}}{\mathop{CH}}\,C{{H}_{2}}Br\]
done
clear
D)
\[HOOC\underset{\begin{smallmatrix} | \\ C{{H}_{3}} \end{smallmatrix}}{\overset{\begin{smallmatrix} C{{H}_{3}} \\ | \end{smallmatrix}}{\mathop{C}}}\,CHCOOH\]
done
clear
E)
\[OHC-CH(OH)-C{{H}_{2}}OH\]
done
clear
View Answer play_arrow
question_answer 79) Which one of the following is an example of homogeneous catalysis?
A)
Haber process of synthesis of ammonia
done
clear
B)
Catalytic conversion of sulphur dioxide to sulphur trioxide in the contact process
done
clear
C)
Catalytic hydrogenation of oils
done
clear
D)
Catalytic conversion of water gas to methanol
done
clear
E)
Acid hydrolysis of methyl acetate
done
clear
View Answer play_arrow
question_answer 80) IUPAC name of \[C{{H}_{3}}CH=\underset{\begin{align} & | \\ & C{{H}_{2}} \\ & | \\ & C{{H}_{3}} \\ \end{align}}{\mathop{C}}\,C{{H}_{3}}\]
A)
2-ethylbutene
done
clear
B)
2-ethylbut-2-ene
done
clear
C)
3-methylpent-2-ene
done
clear
D)
3-methylpent-3-ene
done
clear
E)
3-ethylbut-2-ene
done
clear
View Answer play_arrow
question_answer 81) Which one of the following is not a reducing sugar?
A)
Glucose
done
clear
B)
Lactose
done
clear
C)
Sucrose
done
clear
D)
Maltose
done
clear
E)
Galactose
done
clear
View Answer play_arrow
question_answer 82) If\[p{{K}_{w}}=13.36\]at\[50{}^\circ C,\]the pH of pure water at the same temperature is:
A)
7.00
done
clear
B)
6.68
done
clear
C)
7.63
done
clear
D)
6.00
done
clear
E)
zero
done
clear
View Answer play_arrow
question_answer 83) Which one of the following arrangements of molecules is correct on the basis of their dipole moments?
A)
\[B{{F}_{3}}>N{{F}_{3}}>N{{H}_{3}}\]
done
clear
B)
\[N{{F}_{3}}>B{{F}_{3}}>N{{H}_{3}}\]
done
clear
C)
\[N{{H}_{3}}>B{{F}_{3}}>N{{F}_{3}}\]
done
clear
D)
\[N{{H}_{3}}>N{{F}_{3}}>B{{F}_{3}}\]
done
clear
E)
\[N{{H}_{3}}=N{{F}_{3}}>B{{F}_{3}}\]
done
clear
View Answer play_arrow
question_answer 84) Silver is monovalent and has an atomic mass of 108. Copper is divalent and has an atomic mass of 63.6. The same electric current is passed, for the same length of time through a silver coulometer and a copper coulometer. If 27.0 g of silver is deposited, then the corresponding amount of copper deposited is:
A)
63.60 g
done
clear
B)
31.80 g
done
clear
C)
15.90 g
done
clear
D)
7.95 g
done
clear
E)
4.00 g
done
clear
View Answer play_arrow
question_answer 85) A sample of radioactive substance with half-life of 3 days was found to contain only 3g of it, when received exactly 12 days after sealing. The amount of the radioactive substance when it was sealed, was:
A)
6 g
done
clear
B)
12 g
done
clear
C)
24 g
done
clear
D)
36 g
done
clear
E)
48 g
done
clear
View Answer play_arrow
question_answer 86) Which one of the following sets gives the correct arrangement, based on the thermal stability of the compounds involved?
A)
\[As{{H}_{3}}>P{{H}_{3}}>N{{H}_{3}}\]
done
clear
B)
\[N{{H}_{3}}>P{{H}_{3}}>As{{H}_{3}}\]
done
clear
C)
\[P{{H}_{3}}>N{{H}_{3}}>As{{H}_{3}}\]
done
clear
D)
\[N{{H}_{3}}<As{{H}_{3}}<P{{H}_{3}}\]
done
clear
E)
\[As{{H}_{3}}>N{{H}_{3}}>P{{H}_{3}}\]
done
clear
View Answer play_arrow
question_answer 87) Which one of the following is not a use of potash alum?
A)
As a styptic in arresting bleeding
done
clear
B)
As a pesticide
done
clear
C)
As a mordant in dyeing
done
clear
D)
As a coagulant for colloidal clay in water
done
clear
E)
In leather tanning
done
clear
View Answer play_arrow
question_answer 88) On warming with silver powder, chloroform is converted to:
A)
acetylene
done
clear
B)
hexachloroethane
done
clear
C)
1, 1, 2, 2-tetrachloroethane
done
clear
D)
ethylene
done
clear
E)
carbon
done
clear
View Answer play_arrow
question_answer 89) The temperature at which the vapour pressure of a liquid becomes equal to the external (atmospheric) pressure is its:
A)
melting point
done
clear
B)
sublimation point
done
clear
C)
inversion point
done
clear
D)
critical temperature
done
clear
E)
boiling point
done
clear
View Answer play_arrow
question_answer 90) The salts of which one of the following elements do not impart characteristic colour to the Bunsen flame?
A)
Magnesium
done
clear
B)
Calcium
done
clear
C)
Strontium
done
clear
D)
Sodium
done
clear
E)
Potassium
done
clear
View Answer play_arrow
question_answer 91) The pair of \[[PtC{{l}_{2}}{{(N{{H}_{3}})}_{4}}]B{{r}_{2}}\]and \[[PtB{{r}_{2}}{{(N{{H}_{3}})}_{4}}]C{{l}_{2}}\]constitutes a pair of:
A)
co-ordination isomers
done
clear
B)
linkage isomers
done
clear
C)
ionization isomers
done
clear
D)
hydrate isomers
done
clear
E)
optical isomers
done
clear
View Answer play_arrow
question_answer 92) Natural rubber is a polymer of:
A)
styrene
done
clear
B)
styrene and 1, 3-butadiene
done
clear
C)
tetrafluoroethylene
done
clear
D)
2-methyl 1, 3-butadiene
done
clear
E)
3-methyl 1, 2-butadiene
done
clear
View Answer play_arrow
question_answer 93) At a particular temperature, the vapour pressures of two liquids A and B are respectively 120 and 180 mm of mercury. If 2 moles of A and 3 moles of B are mixed to form an ideal solution, the vapour pressure of the solution at the same temperature will be: (in mm of mercury)
A)
156
done
clear
B)
145
done
clear
C)
150
done
clear
D)
108
done
clear
E)
48
done
clear
View Answer play_arrow
question_answer 94) Which one of the following reactions represents developing in photography?
A)
\[AgN{{O}_{3}}+NaBr\xrightarrow{{}}AgBr+NaN{{O}_{3}}\]
done
clear
B)
\[AgBr+2N{{a}_{2}}{{S}_{2}}{{O}_{3}}\xrightarrow{{}}\]\[N{{a}_{3}}[Ag{{({{S}_{2}}{{O}_{3}})}_{2}}]+NaBr\]
done
clear
C)
\[AgBr+hv\xrightarrow[{}]{{}}AgB{{r}^{*}}\]
done
clear
D)
\[{{C}_{6}}{{H}_{4}}{{(OH)}_{2}}+2AgB{{r}^{*}}\xrightarrow[{}]{{}}{{C}_{6}}{{H}_{4}}{{O}_{2}}\] \[+2HBr+2Ag\]
done
clear
E)
\[AgBr+2N{{H}_{3}}\xrightarrow[{}]{{}}[Ag{{(N{{H}_{3}})}_{2}}]Br\]
done
clear
View Answer play_arrow
question_answer 95) Near the top of blast furnace, used for the extraction of iron, the purified oxide ore is reduced to spongy iron by:
A)
\[C{{O}_{2}}\]
done
clear
B)
\[CO\]
done
clear
C)
limestone
done
clear
D)
aluminium
done
clear
E)
hydrogen
done
clear
View Answer play_arrow
question_answer 96) Which of the following is correct regarding the first ionization potential of Na, Mg, Al and Si?
A)
\[Na<Mg<Al>Si\]
done
clear
B)
\[Na>Mg>Al>Si\]
done
clear
C)
\[Na<Mg<Al<Si\]
done
clear
D)
\[Na>Al<Mg>Si\]
done
clear
E)
\[Na<Al<Mg<Si\]
done
clear
View Answer play_arrow
question_answer 97) The metal that dissolves in liquid ammonia, giving a dark blue coloured solution is:
A)
tin
done
clear
B)
lead
done
clear
C)
sodium
done
clear
D)
silver
done
clear
E)
zinc
done
clear
View Answer play_arrow
question_answer 98) The azo-dye among the following is:
A)
alizarin
done
clear
B)
indigo
done
clear
C)
malachite green
done
clear
D)
martius yellow
done
clear
E)
orange-I
done
clear
View Answer play_arrow
question_answer 99) Graphite is a:
A)
molecular solid
done
clear
B)
covalent solid
done
clear
C)
ionic solid
done
clear
D)
metallic acid
done
clear
E)
amorphous solid
done
clear
View Answer play_arrow
question_answer 100) The law of thermodynamics that provides the basis for the determination of absolute entropy of a substance is:
A)
zeroth law
done
clear
B)
first law
done
clear
C)
second law
done
clear
D)
third law
done
clear
E)
Hesss law
done
clear
View Answer play_arrow
question_answer 101) The boiling point of para nitrophenol is greater than ortho nitrophenol, because:
A)
there is intermolecular hydrogen bonding in para nitrophenol and intramolecular hydrogen bonding in ortho nitrophenol
done
clear
B)
there is intramolecular hydrogen bonding in para nitrophenol and intermolecular hydrogen bonding in ortho nitrophenol
done
clear
C)
both have the same kind of hydrogen bonding
done
clear
D)
para nitrophenol is polar, while ortho nitrophenol is non-polar
done
clear
E)
van der Waals forces are stronger in ortho nitrophenol
done
clear
View Answer play_arrow
question_answer 102) The equilibrium that is not affected by the increase in pressure is:
A)
\[2S{{O}_{2}}(g)+{{O}_{2}}(g)2S{{O}_{3}}(g)\]
done
clear
B)
\[PC{{l}_{3}}(g)+C{{l}_{2}}(g)PC{{l}_{5}}(g)\]
done
clear
C)
\[{{N}_{2}}(g)+3{{H}_{2}}(g)2N{{H}_{3}}(g)\]
done
clear
D)
\[{{N}_{2}}(g)+{{O}_{2}}(g)2NO(g)\]
done
clear
E)
\[2N{{O}_{3}}(g)+{{O}_{2}}(g)2N{{O}_{2}}(g)\]
done
clear
View Answer play_arrow
question_answer 103) The reaction/method that does not give an alkane is:
A)
catalytic hydrogenation of alkenes
done
clear
B)
Wurtz reaction
done
clear
C)
hydrolysis of alkyl magnesium bromide
done
clear
D)
Kolbes electrolytic method
done
clear
E)
dehydrohalogenation of an alkyl halide
done
clear
View Answer play_arrow
question_answer 104) Which one of the following gives a red precipitate with ammoniacal solution of cuprous chloride?
A)
\[{{H}_{3}}CC{{H}_{3}}\]
done
clear
B)
\[{{H}_{2}}C==C{{H}_{2}}\]
done
clear
C)
\[HC\equiv CH\]
done
clear
D)
\[{{H}_{3}}CC=C{{C}_{2}}{{H}_{5}}\]
done
clear
E)
\[{{H}_{5}}{{C}_{6}}C\equiv CC{{H}_{3}}\]
done
clear
View Answer play_arrow
question_answer 105) Rosenmunds reduction of an acylchloride gives:
A)
an aldehyde
done
clear
B)
an alcohol
done
clear
C)
an ester
done
clear
D)
a hydrocarbon
done
clear
E)
an alkyl halide
done
clear
View Answer play_arrow
question_answer 106) The activation energy of a reaction can be determined by:
A)
changing the concentration of the reactants
done
clear
B)
evaluating the rate constant at standard temperature
done
clear
C)
evaluating the rate constant at two different concentrations
done
clear
D)
evaluating the rate constant at two different temperatures
done
clear
E)
by doubling the concentrations of the reactants
done
clear
View Answer play_arrow
question_answer 107) A mixture of sand and sulphur may best be separated by:
A)
fractional method
done
clear
B)
magnetic distillation
done
clear
C)
fractional distillation
done
clear
D)
sublimation
done
clear
E)
dissolving in carbon disulphide and filtering
done
clear
View Answer play_arrow
question_answer 108) The set of numerical coefficients that balances the equation , \[{{K}_{2}}C{{r}_{2}}{{O}_{4}}+HCl\xrightarrow[{}]{{}}{{K}_{2}}C{{r}_{2}}{{O}_{7}}+KCl+{{H}_{2}}O\] is:
A)
1, 1, 2, 2, 1
done
clear
B)
2, 2, 1, 1, 1
done
clear
C)
2, 1, 1, 2, 1
done
clear
D)
2, 2, 1, 2, 1
done
clear
E)
2, 2, 2, 1, 1
done
clear
View Answer play_arrow
question_answer 109) The correct set of quantum numbers for a 4d electron is:
A)
4, 3, 2, +1/2
done
clear
B)
4, 2, 1, 0
done
clear
C)
4, 3,-2, +1/2
done
clear
D)
4, 2, 1,-1/2
done
clear
E)
4, 2, -2, 0
done
clear
View Answer play_arrow
question_answer 110) The heats of combustion of graphite and carbon monoxide, respectively are, \[-\text{ }393.5\text{ }kJ\text{ }mo{{l}^{-1}}\]and\[-283\text{ }kJ\text{ }mo{{l}^{-1}}\]. Therefore, the heat of formation of carbon monoxide in, \[kJ\text{ }mo{{l}^{-1}}\]is:
A)
+172.5
done
clear
B)
\[-110.5\]
done
clear
C)
\[-1070\]
done
clear
D)
\[-676.5\]
done
clear
E)
+ 110.5
done
clear
View Answer play_arrow
question_answer 111) The compound that will form an offensive smell when heated with chloroform and alcoholic potash is:
A)
\[{{C}_{2}}{{H}_{5}}N{{H}_{2}}\]
done
clear
B)
\[{{({{C}_{2}}{{H}_{5}})}_{2}}NH\]
done
clear
C)
\[{{(C{{H}_{3}})}_{3}}N\]
done
clear
D)
\[C{{H}_{3}}CN\]
done
clear
E)
\[{{C}_{6}}{{H}_{5}}CON{{H}_{2}}\]
done
clear
View Answer play_arrow
question_answer 112) The variety of glass used in making lenses and prisms is:
A)
soda glass
done
clear
B)
borosilicate glass
done
clear
C)
flint glass
done
clear
D)
Crookes glass
done
clear
E)
safety glass
done
clear
View Answer play_arrow
question_answer 113) Which one of the following contains the largest number of molecules?
A)
8 g of methane
done
clear
B)
\[16800\text{ }c{{m}^{3}}\]or carbon dioxide at STP
done
clear
C)
14 g of nitrogen
done
clear
D)
4 g of oxygen
done
clear
E)
64 g of sulphur dioxide
done
clear
View Answer play_arrow
question_answer 114) Which of the following aqueous solutions will have the lowest freezing point?
A)
0.1 molal solution of urea
done
clear
B)
0.1 molal solution of sucrose
done
clear
C)
0.1 molal solution of acetic acid
done
clear
D)
0.1 molal solution of sodium chloride
done
clear
E)
0.1 molal solution of calcium chloride
done
clear
View Answer play_arrow
question_answer 115) The reagent that can be used to distinguish between methanoic acid and ethanoic acid is:
A)
ammoniacal silver nitrate solution
done
clear
B)
neutral ferric chloride solution
done
clear
C)
sodium hydroxide solution
done
clear
D)
sodium carbonate solution
done
clear
E)
phenolphthalein
done
clear
View Answer play_arrow
question_answer 116) Across the lanthanide series, the basicity of the lanthanide hydroxides:
A)
increases
done
clear
B)
decreases
done
clear
C)
first increases and then decreases
done
clear
D)
first decreases and then increases
done
clear
E)
does not change
done
clear
View Answer play_arrow
question_answer 117) In the preparation of potassium permanganate, pyrolusite\[(Mn{{O}_{2}})\]is first converted to potassium manganate\[({{K}_{2}}Mn{{O}_{4}})\]. In this conversion, the oxidation state of manganese changes from:
A)
+ 1 to + 3
done
clear
B)
+ 2 to + 4
done
clear
C)
+ 3 to + 5
done
clear
D)
+ 4 to + 6
done
clear
E)
+ 5 to + 7
done
clear
View Answer play_arrow
question_answer 118) The metal that cannot displace hydrogen from dilute hydrochloric acid is:
A)
aluminium
done
clear
B)
iron
done
clear
C)
copper
done
clear
D)
zinc
done
clear
E)
magnesium
done
clear
View Answer play_arrow
question_answer 119) When the sodium fusion extract of an organic compound is treated with lead acetate solution, the formation of a black-precipitate confirms the presence of the element:
A)
nitrogen in the compound
done
clear
B)
sulphur in the compound
done
clear
C)
chlorine in compound
done
clear
D)
bromine in the compound
done
clear
E)
phosphorus in the compound
done
clear
View Answer play_arrow
question_answer 120) When 3 moles of the reactant A and 1 mole of the reactant B are mixed in a vessel of volume 1 L, the following reaction takes place, \[A(g)+B(g)2C(g)\]. If 1.5 moles of C is formed at equilibrium, the equilibrium constant\[({{K}_{c}})\]of the reaction is:
A)
0.12
done
clear
B)
0.50
done
clear
C)
0.25
done
clear
D)
2.25
done
clear
E)
4.00
done
clear
View Answer play_arrow
question_answer 121) The distance of the point\[(2,1,-1)\]from the plane\[x-2y+4z=9\]is:
A)
\[\sqrt{\frac{13}{21}}\]
done
clear
B)
\[\frac{23}{21}\]
done
clear
C)
\[\frac{13}{\sqrt{21}}\]
done
clear
D)
\[\frac{\sqrt{13}}{21}\]
done
clear
E)
None of these
done
clear
View Answer play_arrow
question_answer 122) If the projection of\[\overset{\to }{\mathop{PQ}}\,\]on\[OX,\text{ O}V,\text{ }OZ\]are respectively 12, 3 and 4, then the magnitude of\[\overset{\to }{\mathop{PQ}}\,\]is:
A)
169
done
clear
B)
19
done
clear
C)
13
done
clear
D)
144
done
clear
E)
16
done
clear
View Answer play_arrow
question_answer 123) The shortest distance between the lines \[\frac{x-1}{2}=\frac{y-2}{3}=\frac{z-3}{4}\]and \[\frac{x-2}{3}=\frac{y-4}{4}=\frac{z-5}{5}\]is:
A)
\[\frac{1}{6}\]
done
clear
B)
\[\frac{1}{\sqrt{6}}\]
done
clear
C)
\[\frac{1}{\sqrt{3}}\]
done
clear
D)
\[\frac{1}{3}\]
done
clear
E)
6
done
clear
View Answer play_arrow
question_answer 124) How many terms of the geometric series 1+ 4 + 16 + 64 + ... will make the sum 5461?
A)
7
done
clear
B)
8
done
clear
C)
27
done
clear
D)
28
done
clear
E)
31
done
clear
View Answer play_arrow
question_answer 125) The locus of the point of intersection of two perpendicular tangents to a circle is called:
A)
great circle
done
clear
B)
circumcircle
done
clear
C)
director circle
done
clear
D)
auxiliary circle
done
clear
E)
none of these
done
clear
View Answer play_arrow
question_answer 126) If the circle\[{{x}^{2}}+{{y}^{2}}-17x+2fy+c=0\]passes through (3, 1), (14, 1) and (11, 5), then c is:
A)
0
done
clear
B)
\[-\,41\]
done
clear
C)
\[\frac{-17}{2}\]
done
clear
D)
41
done
clear
E)
\[\frac{17}{4}\]
done
clear
View Answer play_arrow
question_answer 127) The equation of a circle with centre at (1, 0) and circumference 10 n unit, is:
A)
\[{{x}^{2}}+{{y}^{2}}-2x+24=0\]
done
clear
B)
\[{{x}^{2}}+{{y}^{2}}-x-25=0\]
done
clear
C)
\[{{x}^{2}}+{{y}^{2}}-2x-24=0\]
done
clear
D)
\[{{x}^{2}}+{{y}^{2}}+2x+24=0\]
done
clear
E)
\[{{x}^{2}}+{{y}^{2}}-2y+24=0\]
done
clear
View Answer play_arrow
question_answer 128) The foot of the perpendicular from\[(-2,3)\]to the line\[2x-y=0\]:
A)
\[(-2,3)\]
done
clear
B)
(2, 1)
done
clear
C)
(3, 2)
done
clear
D)
(1, 2)
done
clear
E)
\[(-3,-2)\]
done
clear
View Answer play_arrow
question_answer 129) The circles\[{{x}^{2}}+{{y}^{2}}+2ax+c=0\]and \[{{x}^{2}}+{{y}^{2}}+2by+c=0\]touches, if:
A)
\[\frac{1}{a}+\frac{1}{b}=\frac{1}{c}\]
done
clear
B)
\[\frac{1}{{{a}^{2}}}+\frac{1}{{{b}^{2}}}=\frac{1}{c}\]
done
clear
C)
\[\frac{1}{{{a}^{2}}}+\frac{1}{{{b}^{2}}}=\frac{1}{{{c}^{2}}}\]
done
clear
D)
\[\frac{1}{{{a}^{2}}}-\frac{1}{{{b}^{2}}}-\frac{1}{c}\]
done
clear
E)
\[\frac{1}{a}+\frac{1}{b}=\frac{1}{{{c}^{2}}}\]
done
clear
View Answer play_arrow
question_answer 130) If\[r=2a\cos \theta \]represents a circle, then its centre is:
A)
\[(0,-a)\]
done
clear
B)
(a, a)
done
clear
C)
\[(-a,0)\]
done
clear
D)
(a, 0)
done
clear
E)
(0, a)
done
clear
View Answer play_arrow
question_answer 131) kIf the lines\[x-y-1=0,4x+3y=k\]and \[2x-3y+1=0\]are concurrent, then k is:
A)
1
done
clear
B)
\[-1\]
done
clear
C)
25
done
clear
D)
5
done
clear
E)
\[-20\]
done
clear
View Answer play_arrow
question_answer 132) The number of common tangents to the circles\[{{x}^{2}}+{{y}^{2}}=4\]and\[{{x}^{2}}+{{y}^{2}}-8x+12=0\]is:
A)
1
done
clear
B)
2
done
clear
C)
3
done
clear
D)
4
done
clear
E)
none of these
done
clear
View Answer play_arrow
question_answer 133) The centroid of a triangle formed by the points (0, 0),\[(cos\text{ }\theta ,\text{ }sin\text{ }\theta )\]and\[(sin\text{ }\theta -cos\text{ }\theta )\]lie on the line\[y=2x;\]then\[\theta \]is:
A)
\[{{\tan }^{-1}}2\]
done
clear
B)
\[{{\tan }^{-1}}\frac{1}{3}\]
done
clear
C)
\[{{\tan }^{-1}}\frac{1}{2}\]
done
clear
D)
\[{{\tan }^{-1}}(-2)\]
done
clear
E)
\[{{\tan }^{-1}}(-3)\]
done
clear
View Answer play_arrow
question_answer 134) The orthocentre of the triangle formed by (8,0) and (4, 6) with the origin, is:
A)
\[\left( 4,\frac{8}{3} \right)\]
done
clear
B)
\[(3,-4)\]
done
clear
C)
\[(4,3)\]
done
clear
D)
\[(3,4)\]
done
clear
E)
\[\left( \frac{8}{3},4 \right)\]
done
clear
View Answer play_arrow
question_answer 135) If the angle between two lines represented by \[2{{x}^{2}}+5xy+3{{y}^{2}}+7y+4=0\]is\[ta{{n}^{-1}}m,\]then m is equal to:
A)
\[\frac{1}{5}\]
done
clear
B)
1
done
clear
C)
\[\frac{7}{5}\]
done
clear
D)
7
done
clear
E)
none of these
done
clear
View Answer play_arrow
question_answer 136) If\[xy-4x+3y-\lambda =0\]represents the asymptotes of\[xy-4x+3y=0,\]then\[\lambda \]is:
A)
3
done
clear
B)
\[-\,6\]
done
clear
C)
8
done
clear
D)
12
done
clear
E)
4
done
clear
View Answer play_arrow
question_answer 137) The equation of the chord of the parabola \[{{y}^{2}}=8x\]which is bisected at the point\[(2,-3),\]is:
A)
\[4x+3y+1=0\]
done
clear
B)
\[3x+4y-1=0\]
done
clear
C)
\[4x-3y-1=0\]
done
clear
D)
\[3x-4y+1=0\]
done
clear
E)
\[4x+3y=0\]
done
clear
View Answer play_arrow
question_answer 138) If\[x+y+1=0\]touches the parabola\[{{y}^{2}}=\lambda x,\] then K is equal to:
A)
2
done
clear
B)
4
done
clear
C)
6
done
clear
D)
8
done
clear
E)
none of these
done
clear
View Answer play_arrow
question_answer 139) The equations\[x=\frac{{{e}^{t}}+{{e}^{-t}}}{2},y=\frac{{{e}^{t}}-{{e}^{-t}}}{2}\]where t is real number, represents:
A)
an ellipse
done
clear
B)
a parabola
done
clear
C)
a hyperbola
done
clear
D)
a circle
done
clear
E)
none of these
done
clear
View Answer play_arrow
question_answer 140) If\[{{e}_{1}}\]and\[{{e}_{2}}\]are the eccentricities of two conies with\[e_{1}^{2}+e_{2}^{2}=3,\]then the conies are:
A)
ellipses
done
clear
B)
parabolas
done
clear
C)
circles
done
clear
D)
hyperbolas
done
clear
E)
none of these
done
clear
View Answer play_arrow
question_answer 141) The sum of the distances of any point on the ellipse\[3{{x}^{2}}+4{{y}^{2}}=24\]from its foci, is:
A)
\[8\sqrt{2}\]
done
clear
B)
8
done
clear
C)
\[16\sqrt{2}\]
done
clear
D)
\[2\sqrt{2}\]
done
clear
E)
\[4\sqrt{2}\]
done
clear
View Answer play_arrow
question_answer 142) In\[\Delta ABC,\]if a tends to 2 c and b tends to 3 c, then\[cos\text{ }B\]tends to:
A)
\[-1\]
done
clear
B)
\[\frac{1}{2}\]
done
clear
C)
\[\frac{1}{3}\]
done
clear
D)
\[\frac{2}{3}\]
done
clear
E)
1
done
clear
View Answer play_arrow
question_answer 143) If\[\sin (\pi \cos \theta )=\cos (\pi s\sin \theta ),\]then which of the following is correct?
A)
\[\cos \theta =\frac{3}{2\sqrt{2}}\]
done
clear
B)
\[\cos \left( \theta -\frac{\pi }{2} \right)=\frac{1}{2\sqrt{2}}\]
done
clear
C)
\[\cos \left( \theta -\frac{\pi }{4} \right)=\frac{1}{2\sqrt{2}}\]
done
clear
D)
\[\cos \left( \theta +\frac{\pi }{4} \right)=-\frac{1}{2\sqrt{2}}\]
done
clear
E)
\[\cos \left( \theta +\frac{\pi }{4} \right)=\frac{1}{2}\]
done
clear
View Answer play_arrow
question_answer 144) The value of\[sin\text{ }12{}^\circ \text{ }sin\text{ }48{}^\circ \text{ }sin\text{ }54{}^\circ \]is equal to:
A)
\[\frac{2}{3}\]
done
clear
B)
\[\frac{1}{2}\]
done
clear
C)
\[\frac{1}{8}\]
done
clear
D)
\[\frac{1}{3}\]
done
clear
E)
3
done
clear
View Answer play_arrow
question_answer 145) If\[3{{\sin }^{-1}}\left( \frac{2x}{1+{{x}^{2}}} \right)-4{{\cos }^{-1}}\left( \frac{1-{{x}^{2}}}{1+{{x}^{2}}} \right)\]\[+2{{\tan }^{-1}}\left( \frac{2x}{1-{{x}^{2}}} \right)=\frac{\pi }{3},\]then\[x\]is equal to:
A)
\[\frac{1}{\sqrt{3}}\]
done
clear
B)
\[-\frac{1}{\sqrt{3}}\]
done
clear
C)
\[\sqrt{3}\]
done
clear
D)
\[-\frac{\sqrt{3}}{2}\]
done
clear
E)
\[\frac{\sqrt{3}}{2}\]
done
clear
View Answer play_arrow
question_answer 146) The shadow of a pole is\[\sqrt{3}\]times longer. The angle of elevation is equal to:
A)
\[40{}^\circ \]
done
clear
B)
\[\frac{45{}^\circ }{2}\]
done
clear
C)
\[60{}^\circ \]
done
clear
D)
\[30{}^\circ \]
done
clear
E)
\[90{}^\circ \]
done
clear
View Answer play_arrow
question_answer 147) The point of contact of the line\[x-y+2=0\]with the parabola\[{{y}^{2}}-8x=0\]is:
A)
(2, 4)
done
clear
B)
\[(-2,4)\]
done
clear
C)
\[(2,-4)\]
done
clear
D)
(2, 2)
done
clear
E)
(6, 8)
done
clear
View Answer play_arrow
question_answer 148) If the sides of a triangle are\[{{x}^{2}}+x+1,\]\[{{x}^{2}}-1\]and\[2x+1,\]then the greatest angle is:
A)
\[90{}^\circ \]
done
clear
B)
\[135{}^\circ \]
done
clear
C)
\[115{}^\circ \]
done
clear
D)
\[105{}^\circ \]
done
clear
E)
\[120{}^\circ \]
done
clear
View Answer play_arrow
question_answer 149) The value of\[\cos 1{}^\circ .\cos 2{}^\circ .\cos 3{}^\circ .....\cos 179{}^\circ \]is equal to:
A)
\[\frac{1}{\sqrt{2}}\]
done
clear
B)
\[0\]
done
clear
C)
\[1\]
done
clear
D)
\[-1\]
done
clear
E)
\[-\frac{1}{\sqrt{2}}\]
done
clear
View Answer play_arrow
question_answer 150) If\[\cot (\alpha +\beta )=0,\]then\[\sin (\alpha +2\beta )\]is equal to:
A)
\[\sin \alpha \]
done
clear
B)
\[\cos \alpha \]
done
clear
C)
\[\sin \beta \]
done
clear
D)
\[\cos 2\beta \]
done
clear
E)
\[\sin 2\alpha \]
done
clear
View Answer play_arrow
question_answer 151) The value of\[4\text{ }sin\text{ }A\text{ }co{{s}^{3}}A-4\text{ }cos\text{ }A\text{ }si{{n}^{3}}A\]is equal to:
A)
\[cos\text{ }2A\]
done
clear
B)
\[sin\text{ }3A\]
done
clear
C)
\[sin\text{ }2A\]
done
clear
D)
\[cos\text{ }4A\]
done
clear
E)
\[sin\text{ }4A\]
done
clear
View Answer play_arrow
question_answer 152) If the solutions for\[\theta \]of \[\cos p\theta +\cos q\theta =0,p>q>0\]are in AP, then the numerically smallest common difference of AP is:
A)
\[-\frac{\pi }{p+q}\]
done
clear
B)
\[\frac{2\pi }{p+q}\]
done
clear
C)
\[\frac{\pi }{2(p+q)}\]
done
clear
D)
\[\frac{1}{p+q}\]
done
clear
E)
\[\frac{1}{2(p+q)}\]
done
clear
View Answer play_arrow
question_answer 153) The value of k for which \[{{(cos\text{ }x+sin\text{ }x)}^{2}}+k\text{ }sin\text{ }x\,cos\text{ }x-1=0\]is an identity, is:
A)
\[-1\]
done
clear
B)
\[-2\]
done
clear
C)
0
done
clear
D)
1
done
clear
E)
2
done
clear
View Answer play_arrow
question_answer 154) If\[4{{\cos }^{-1}}x+{{\sin }^{-1}}x=\pi ,\]then the value of\[x\]is:
A)
\[\frac{1}{2}\]
done
clear
B)
\[\frac{1}{\sqrt{2}}\]
done
clear
C)
\[\frac{\sqrt{3}}{2}\]
done
clear
D)
\[\frac{2}{\sqrt{3}}\]
done
clear
E)
\[\frac{3}{2}\]
done
clear
View Answer play_arrow
question_answer 155) A problem in mathematics is given to 3 students whose chances of solving individually are\[\frac{1}{2},\frac{1}{3}\]and\[\frac{1}{4}\]. The probability that the problem will be solved at least by one, is;
A)
\[\frac{1}{4}\]
done
clear
B)
\[\frac{1}{24}\]
done
clear
C)
\[\frac{23}{24}\]
done
clear
D)
\[\frac{3}{4}\]
done
clear
E)
\[1\]
done
clear
View Answer play_arrow
question_answer 156) In a non-leap year the probability of getting 53 Sundays or 53 Tuesdays or 53 Thursdays is:
A)
\[\frac{1}{7}\]
done
clear
B)
\[\frac{2}{7}\]
done
clear
C)
\[\frac{3}{7}\]
done
clear
D)
\[\frac{4}{7}\]
done
clear
E)
\[\frac{1}{53}\]
done
clear
View Answer play_arrow
question_answer 157) The probability for a randomly chosen month to have its 10th day as Sunday, is:
A)
\[\frac{1}{84}\]
done
clear
B)
\[\frac{10}{12}\]
done
clear
C)
\[\frac{10}{84}\]
done
clear
D)
\[\frac{1}{7}\]
done
clear
E)
\[\frac{1}{12}\]
done
clear
View Answer play_arrow
question_answer 158) If the mean of numbers\[27+x,\text{ }31+x,\]\[89+x,\] \[107+x,\text{ }156+x\]is 82, then the mean of \[130+x,\text{ }126+x,\text{ }68+x,\text{ }50+x,\text{ }1+x\]is:
A)
79
done
clear
B)
157
done
clear
C)
82
done
clear
D)
80
done
clear
E)
75
done
clear
View Answer play_arrow
question_answer 159) If\[\mu \]is the mean distribution of\[\{{{y}_{i}},{{f}_{i}}\},\]then\[\Sigma {{f}_{i}}\{{{y}_{i}}-\mu \}\]is equal to:
A)
MD
done
clear
B)
SD
done
clear
C)
0
done
clear
D)
relative frequency
done
clear
E)
none of these
done
clear
View Answer play_arrow
question_answer 160) Two cards are drawn successively with replacement from a well-shuffled pack of 52 cards. The probability of drawing two aces is:
A)
\[\frac{1}{13}\]
done
clear
B)
\[\frac{1}{13}\times \frac{1}{17}\]
done
clear
C)
\[\frac{1}{52}\times \frac{1}{51}\]
done
clear
D)
\[\frac{1}{13}\times \frac{4}{51}\]
done
clear
E)
\[\frac{1}{13}\times \frac{1}{13}\]
done
clear
View Answer play_arrow
question_answer 161) If\[\sec \left( \frac{x+y}{x-y} \right)=a,\]then\[\frac{dy}{dx}\]is equal to:
A)
\[\frac{x}{y}\]
done
clear
B)
\[\frac{y}{x}\]
done
clear
C)
\[y\]
done
clear
D)
\[x\]
done
clear
E)
\[\frac{x}{a}\]
done
clear
View Answer play_arrow
question_answer 162) If\[{{x}^{y}}={{e}^{x-y}},\]then\[\frac{dy}{dx}\]is equal to:
A)
\[\frac{\log x}{1+\log x}\]
done
clear
B)
\[\frac{\log x}{1-\log x}\]
done
clear
C)
\[\frac{\log x}{{{(1+\log x)}^{2}}}\]
done
clear
D)
\[\frac{y\log x}{x(1+\log x)}\]
done
clear
E)
\[\frac{1+\log x}{\log x}\]
done
clear
View Answer play_arrow
question_answer 163) For \[y=\cos (m{{\sin }^{-1}}x)\]which of the following is true?
A)
\[(1-{{x}^{2}}){{y}_{2}}+x{{y}_{1}}-{{m}^{2}}y=0\]
done
clear
B)
\[(1-{{x}^{2}}){{y}_{2}}-x{{y}_{1}}+{{m}^{2}}y=0\]
done
clear
C)
\[(1+{{x}^{2}}){{y}_{2}}+x{{y}_{1}}-{{m}^{2}}y=0\]
done
clear
D)
\[(1-{{x}^{2}}){{y}_{2}}+x{{y}_{1}}+{{m}^{2}}y=0\]
done
clear
E)
\[(1-x){{y}_{2}}-x{{y}_{1}}+{{m}^{2}}y=0\]
done
clear
View Answer play_arrow
question_answer 164) If \[f(x)=\left\{ \begin{matrix} x+1, & x\le 1 \\ 3-a{{x}^{2}}, & x>1 \\ \end{matrix} \right.\]is continuous at\[x=1,\]then the value of a is:
A)
\[-1\]
done
clear
B)
2
done
clear
C)
\[-3\]
done
clear
D)
\[-2\]
done
clear
E)
1
done
clear
View Answer play_arrow
question_answer 165) \[\underset{x\to \frac{\pi }{2}}{\mathop{\lim }}\,\frac{{{a}^{\cot x}}-{{a}^{\cos x}}}{\cot x-\cos x}\]is equal to:
A)
\[log\text{ }a\]
done
clear
B)
\[log\text{ }2\]
done
clear
C)
\[a\]
done
clear
D)
\[log\text{ }x\]
done
clear
E)
none of these
done
clear
View Answer play_arrow
question_answer 166) If\[f\,(0)=k,\]then \[\underset{x\to 0}{\mathop{\lim }}\,\frac{2f(x)-3f(2x)+f(4x)}{{{x}^{2}}}\]is equal to:
A)
\[k\]
done
clear
B)
\[2k\]
done
clear
C)
\[3k\]
done
clear
D)
\[4k\]
done
clear
E)
\[\frac{k}{3}\]
done
clear
View Answer play_arrow
question_answer 167) If g is the inverse function of\[f\]and \[f(x)=\frac{1}{1+{{x}^{n}}},\]then\[g(x)\]is equal to:
A)
\[i+{{(g(x))}^{n}}\]
done
clear
B)
\[1-g(x)\]
done
clear
C)
\[1+g(x)\]
done
clear
D)
\[1-{{(g(x))}^{n}}\]
done
clear
E)
\[{{(g(x))}^{n}}\]
done
clear
View Answer play_arrow
question_answer 168) The curves\[4{{x}^{2}}+9{{y}^{2}}=72\]and\[{{x}^{2}}-{{y}^{2}}=5\]at (3, 2):
A)
touch each other
done
clear
B)
cut orthogonally
done
clear
C)
intersect at\[45{}^\circ \]
done
clear
D)
intersect at\[60{}^\circ \]
done
clear
E)
none of these
done
clear
View Answer play_arrow
question_answer 169) The velocity v m/s of a particle is proportional to the cube of the time. If the velocity after 2 s is 4m/s, then v is equal to:
A)
\[{{t}^{3}}\]
done
clear
B)
\[\frac{{{t}^{3}}}{2}\]
done
clear
C)
\[\frac{{{t}^{3}}}{3}\]
done
clear
D)
\[\frac{{{t}^{3}}}{4}\]
done
clear
E)
\[\frac{{{t}^{2}}}{2}\]
done
clear
View Answer play_arrow
question_answer 170) The minimum value of\[x\text{ }log\text{ }x\]is equal to:
A)
\[e\]
done
clear
B)
\[\frac{1}{e}\]
done
clear
C)
\[-\frac{1}{e}\]
done
clear
D)
\[\frac{2}{e}\]
done
clear
E)
\[-e\]
done
clear
View Answer play_arrow
question_answer 171) A particle moves along the\[x-\]axis so that it position is given\[x=2{{t}^{3}}-3{{t}^{2}}\] at a time t seconds. What is the time interval during which particle will be on the negative half of the axis?
A)
\[0<t<\frac{2}{3}\]
done
clear
B)
\[0<t<1\]
done
clear
C)
\[0<t<\frac{3}{2}\]
done
clear
D)
\[\frac{1}{2}<t<1\]
done
clear
E)
\[1<t<\frac{3}{2}\]
done
clear
View Answer play_arrow
question_answer 172) A stone thrown vertically upwards satisfies the equations\[s=80t-16\text{ }{{\text{t}}^{2}}\]. The time required to reach the maximum height is:
A)
2s
done
clear
B)
4 s
done
clear
C)
3 s
done
clear
D)
3.5 s
done
clear
E)
2.5 s
done
clear
View Answer play_arrow
question_answer 173) If \[f(x+y)=f(x).f(y),f(3)=3,\]\[f(0)=11\]then\[f(3)\]is equal to:
A)
\[11.{{e}^{33}}\]
done
clear
B)
33
done
clear
C)
11
done
clear
D)
log 33
done
clear
E)
none of these
done
clear
View Answer play_arrow
question_answer 174) If\[y=x\text{ }tan\text{ }y,\]then\[\frac{dy}{dx}\]is equal to:
A)
\[\frac{\tan y}{x-{{x}^{2}}-{{y}^{2}}}\]
done
clear
B)
\[\frac{y}{x-{{x}^{2}}-{{y}^{2}}}\]
done
clear
C)
\[\frac{\tan y}{y-x}\]
done
clear
D)
\[\frac{\tan x}{x-{{y}^{2}}}\]
done
clear
E)
\[\frac{\tan y}{x+{{x}^{2}}+{{y}^{2}}}\]
done
clear
View Answer play_arrow
question_answer 175) The product of the lengths of subtangent and subnormal at any point\[(x,\text{ }y)\]of a curve is:
A)
\[{{x}^{2}}\]
done
clear
B)
\[{{y}^{2}}\]
done
clear
C)
a constant
done
clear
D)
\[x\]
done
clear
E)
\[y\]
done
clear
View Answer play_arrow
question_answer 176) The equation of tangent to the curve\[{{\left( \frac{x}{a} \right)}^{n}}+{{\left( \frac{y}{b} \right)}^{n}}=2\]at\[(a,b)\]is:
A)
\[\frac{x}{a}+\frac{y}{b}=2\]
done
clear
B)
\[\frac{x}{a}+\frac{y}{b}=\frac{1}{2}\]
done
clear
C)
\[\frac{x}{b}-\frac{y}{a}=2\]
done
clear
D)
\[ax+by=2\]
done
clear
E)
\[ax-by=2\]
done
clear
View Answer play_arrow
question_answer 177) If\[\int_{0}^{\infty }{\frac{{{x}^{2}}dx}{({{x}^{2}}+{{a}^{2}})({{x}^{2}}+{{b}^{2}})({{x}^{2}}+{{c}^{2}})}}\]\[=\frac{\pi }{2(a+b)(b+c)(c+a)},\]then the value of\[\int_{0}^{\infty }{\frac{1}{({{x}^{2}}+4)({{x}^{2}}+9)}}dx\]is:
A)
\[\frac{\pi }{60}\]
done
clear
B)
\[\frac{\pi }{20}\]
done
clear
C)
\[\frac{\pi }{40}\]
done
clear
D)
\[\frac{\pi }{80}\]
done
clear
E)
\[\frac{\pi }{10}\]
done
clear
View Answer play_arrow
question_answer 178) \[\int{({{e}^{a\log x}}+{{e}^{x\log a}})}dx\]is equal to:
A)
\[\frac{{{x}^{a+1}}}{a+1}+c\]
done
clear
B)
\[\frac{{{x}^{a+1}}}{a+1}+\frac{{{a}^{x}}}{\log a}+c\]
done
clear
C)
\[{{x}^{a+1}}+{{a}^{x}}+c\]
done
clear
D)
\[\frac{{{x}^{a+1}}}{a-1}+\frac{\log a}{{{a}^{x}}}+c\]
done
clear
E)
\[\frac{{{x}^{a+1}}}{a+1}-\frac{{{a}^{x}}}{\log a}+c\]
done
clear
View Answer play_arrow
question_answer 179) \[\int_{0}^{a}{\frac{dx}{x+\sqrt{{{d}^{2}}-{{x}^{2}}}}}\] is:
A)
\[\frac{{{a}^{2}}}{4}\]
done
clear
B)
\[\frac{\pi }{2}\]
done
clear
C)
\[\frac{\pi }{4}\]
done
clear
D)
\[\pi \]
done
clear
E)
\[\frac{{{\pi }^{2}}}{4}\]
done
clear
View Answer play_arrow
question_answer 180) If\[\int_{-1}^{4}{f(x)}dx=4\]and\[\int_{2}^{4}{[3-f(x)]}dx=7,\]then the value of\[\int_{-1}^{2}{f(x)}\,dx\]is:
A)
\[-2\]
done
clear
B)
3
done
clear
C)
5
done
clear
D)
8
done
clear
E)
\[-1\]
done
clear
View Answer play_arrow
question_answer 181) \[\underset{n\to \infty }{\mathop{\lim }}\,\left( \frac{1}{\sqrt{4{{n}^{2}}-1}}+\frac{1}{\sqrt{4{{n}^{2}}-{{2}^{2}}}}+...+\frac{1}{\sqrt{3{{n}^{2}}}} \right)\]is equal to:
A)
\[0\]
done
clear
B)
\[1\]
done
clear
C)
\[\frac{\pi }{3}\]
done
clear
D)
\[\frac{\pi }{6}\]
done
clear
E)
\[\frac{2\pi }{3}\]
done
clear
View Answer play_arrow
question_answer 182) The area bounded by\[y=1+\frac{8}{{{x}^{2}}}\]and the ordinates\[x=2\]and\[x=4\]is:
A)
2 sq unit
done
clear
B)
4 sq unit
done
clear
C)
\[log\text{ }2\]sq unit
done
clear
D)
\[log\text{ }4\]sq unit
done
clear
E)
8 sq unit
done
clear
View Answer play_arrow
question_answer 183) The value of \[\int_{0}^{1}{\left[ 1-\frac{x}{1!}+\frac{{{x}^{2}}}{2!}-\frac{{{x}^{3}}}{3!}+...+\frac{{{(-1)}^{n}}{{x}^{n}}}{n!}+.... \right]}\] \[\times e{{x}^{2}}dx\]:
A)
0
done
clear
B)
\[e-1\]
done
clear
C)
1
done
clear
D)
e
done
clear
E)
none of these
done
clear
View Answer play_arrow
question_answer 184) The value of\[\int_{0}^{1}{x\,{{(1-x)}^{99}}}\,dx\]is equal to:
A)
\[\frac{1}{10100}\]
done
clear
B)
\[\frac{11}{10100}\]
done
clear
C)
\[\frac{1}{10010}\]
done
clear
D)
\[\frac{11}{11100}\]
done
clear
E)
\[\frac{1}{1010}\]
done
clear
View Answer play_arrow
question_answer 185) The area bounded by the curve \[y={{x}^{4}}-2{{x}^{3}}+{{x}^{2}}+3\] with\[x-\]axis and ordinates corresponding to the minima of y is:
A)
1 sq unit
done
clear
B)
\[\frac{91}{30}sq\text{ }unit\]
done
clear
C)
\[\frac{30}{9}sq\text{ }unit\]
done
clear
D)
\[4sq\text{ }unit\]
done
clear
E)
\[\frac{30}{91}sq\text{ }unit\]
done
clear
View Answer play_arrow
question_answer 186) If\[\int_{0}^{1}{\frac{{{e}^{-x}}dx}{1+{{e}^{x}}}}={{\log }_{e}}(1+e)+k,\]then k is equal to:
A)
\[{{e}^{-1}}+\log 2\]
done
clear
B)
\[-(e+\log 2)\]
done
clear
C)
\[-\left( \frac{1}{e}+\log 2 \right)\]
done
clear
D)
\[-({{e}^{-1}}+\log 3)\]
done
clear
E)
\[-(e+\log 3)\]
done
clear
View Answer play_arrow
question_answer 187) The value of\[\int{\frac{{{e}^{x}}(2-{{x}^{2}})dx}{(1-x)\sqrt{1-{{x}^{2}}}}}\]is equal to:
A)
\[{{e}^{x}}\sqrt{\frac{1+x}{1-x}}+c\]
done
clear
B)
\[{{e}^{x}}\sqrt{1+x}+c\]
done
clear
C)
\[{{e}^{x}}\sqrt{1-x}+c\]
done
clear
D)
\[{{e}^{x}}\sqrt{\frac{1-x}{1+x}}+c\]
done
clear
E)
\[\sqrt{\frac{1+x}{1-x}}+c\]
done
clear
View Answer play_arrow
question_answer 188) If\[u=\log ({{x}^{3}}+{{y}^{3}}+{{z}^{3}}-3xyz),\] then \[(x,y,z)\left( \frac{\partial u}{\partial x}+\frac{\partial u}{\partial y}+\frac{\partial u}{\partial z} \right)\]is equal to:
A)
0
done
clear
B)
1
done
clear
C)
\[u\]
done
clear
D)
3
done
clear
E)
\[-1\]
done
clear
View Answer play_arrow
question_answer 189) The order and degree of the differential equation\[\frac{{{d}^{2}}y}{d{{x}^{2}}}={{\left\{ 1+{{\left( \frac{dy}{dx} \right)}^{2}} \right\}}^{\frac{3}{2}}}\]. are:
A)
2, 2
done
clear
B)
2, 1
done
clear
C)
1, 2
done
clear
D)
2, 3
done
clear
E)
1, 3
done
clear
View Answer play_arrow
question_answer 190) The general solution of \[{{e}^{x}}\cos ydx-{{e}^{x}}\sin y\,dy=0\]is:
A)
\[{{e}^{x}}(\sin y+\cos y)=c\]
done
clear
B)
\[{{e}^{x}}\sin y=c\]
done
clear
C)
\[{{e}^{x}}=c\cos y\]
done
clear
D)
\[{{e}^{x}}=c\sin y\]
done
clear
E)
\[{{e}^{x}}\cos y=c\]
done
clear
View Answer play_arrow
question_answer 191) The equation of a curve passing through the origin and satisfying the differential equation \[\frac{dy}{dx}={{(x-y)}^{2}}\]is:
A)
\[{{e}^{2x}}(1-x+y)=1+x-y\]
done
clear
B)
\[{{e}^{2x}}(1+x-y)=1-x+y\]
done
clear
C)
\[{{e}^{2x}}(1-x+y)+(1+x-y)=0\]
done
clear
D)
\[{{e}^{2x}}(1+x+y)=1-x+y\]
done
clear
E)
none of the above
done
clear
View Answer play_arrow
question_answer 192) The differential equation\[y\frac{dy}{dx}+x=c\]represents:
A)
a family of hyperbolas
done
clear
B)
a family of circles whose centres are on the y-axis
done
clear
C)
a family of parabolas
done
clear
D)
a family of ellipse
done
clear
E)
a family of circles whose centres are on the x-axis
done
clear
View Answer play_arrow
question_answer 193) The general solution of \[ydx-xdy-3{{x}^{2}}{{y}^{2}}{{e}^{{{x}^{3}}}}dx=0\]is equal to:
A)
\[\frac{x}{y}={{e}^{{{x}^{3}}}}+c\]
done
clear
B)
\[\frac{y}{x}={{e}^{x}}+c\]
done
clear
C)
\[xy={{e}^{{{x}^{2}}}}+c\]
done
clear
D)
\[xy\,{{e}^{{{x}^{3}}}}=c\]
done
clear
E)
\[xy={{e}^{{{x}^{3}}}}+c\]
done
clear
View Answer play_arrow
question_answer 194) \[{{\tan }^{-1}}x+{{\tan }^{-1}}y=c\]is general solution of the differential equation:
A)
\[\frac{dy}{dx}=\frac{1+{{y}^{2}}}{1+{{x}^{2}}}\]
done
clear
B)
\[\frac{dy}{dx}=\frac{1+{{x}^{2}}}{1+{{y}^{2}}}\]
done
clear
C)
\[(1+{{x}^{2}})dy+(1+{{y}^{2}})dx=0\]
done
clear
D)
\[\frac{dy}{dx}=\frac{1-{{y}^{2}}}{1-{{x}^{2}}}\]
done
clear
E)
\[(1-{{x}^{2}})dx+(1-y)dy=0\]
done
clear
View Answer play_arrow
question_answer 195) If A and B are not disjoint sets, then\[n(A\cup B)\]is equal to:
A)
\[n(A)+n(B)\]
done
clear
B)
\[n(A)+n(B)-n(A\cap B)\]
done
clear
C)
\[n(A)+n(B)+n(A\cap B)\]
done
clear
D)
\[n(A)\,n(B)\]
done
clear
E)
\[n(A)-n(B)\]
done
clear
View Answer play_arrow
question_answer 196) If\[x\ne 1\]and\[f(x)=\frac{x+1}{x-1}\]is a real function, then \[fff(2)\]is:
A)
1
done
clear
B)
2
done
clear
C)
3
done
clear
D)
4
done
clear
E)
none of these
done
clear
View Answer play_arrow
question_answer 197) The domain of\[{{\sin }^{-1}}\left( \frac{2x+1}{3} \right)\]is:
A)
\[(2,-1)\]
done
clear
B)
\[[-2,1]\]
done
clear
C)
R
done
clear
D)
\[(-1,1)\]
done
clear
E)
\[(-2,\text{ }0)\]
done
clear
View Answer play_arrow
question_answer 198) If\[f(x)=\cos (\log x),\]then \[f\left( \frac{1}{x} \right)f\left( \frac{1}{y} \right)-\frac{1}{2}\left[ f\left( \frac{x}{y} \right)+f(xy) \right]\]to:
A)
\[\cos (x-y)\]
done
clear
B)
\[\log [\cos (x+y)]\]
done
clear
C)
\[1\]
done
clear
D)
\[0\]
done
clear
E)
\[\cos (x+y)\]
done
clear
View Answer play_arrow
question_answer 199) The value of\[{{\left( \frac{-1+\sqrt{-3}}{2} \right)}^{26}}+{{\left( \frac{-1-\sqrt{-3}}{2} \right)}^{26}}\]is:
A)
\[-1\]
done
clear
B)
1
done
clear
C)
0
done
clear
D)
2
done
clear
E)
none of these
done
clear
View Answer play_arrow
question_answer 200) If\[{{(\sqrt{3}-i)}^{50}}={{2}^{48}}(x-iy),\]then\[{{x}^{2}}+{{y}^{2}}\]is equal to:
A)
2
done
clear
B)
4
done
clear
C)
8
done
clear
D)
16
done
clear
E)
32
done
clear
View Answer play_arrow
question_answer 201) If \[1,\omega ,{{\omega }^{2}}\]are cube roots of unity, then \[{{(1+\omega )}^{3}}-1{{(1+{{\omega }^{2}})}^{3}}\]is:
A)
0
done
clear
B)
\[-1\]
done
clear
C)
\[\omega \]
done
clear
D)
2
done
clear
E)
\[-2\]
done
clear
View Answer play_arrow
question_answer 202) If\[\left| \frac{z-i}{z+i} \right|=1,\]then the locus of 2 is:
A)
\[x=0\]
done
clear
B)
\[y=0\]
done
clear
C)
\[x=1\]
done
clear
D)
\[y=1\]
done
clear
E)
none of these
done
clear
View Answer play_arrow
question_answer 203) The condition that one root of the equation \[a{{x}^{2}}+bx+c=0\]be square of the other, is:
A)
\[{{a}^{2}}c+a{{c}^{2}}+{{b}^{3}}-3abc=0\]
done
clear
B)
\[{{a}^{2}}{{c}^{2}}+a{{c}^{2}}+{{b}^{2}}-3abc=0\]
done
clear
C)
\[a{{c}^{2}}+ac+{{b}^{3}}-3abc=0\]
done
clear
D)
\[{{a}^{2}}c+a{{c}^{2}}-{{b}^{3}}-3abc=0\]
done
clear
E)
\[ac+{{b}^{3}}-3abc=0\]
done
clear
View Answer play_arrow
question_answer 204) If \[\alpha \] and \[\beta \] are roots of the equation\[4{{x}^{2}}+2x-1=0,\]then the value of\[{{\alpha }^{2}}+{{\beta }^{2}}\]is:
A)
2
done
clear
B)
\[\frac{3}{4}\]
done
clear
C)
\[3\]
done
clear
D)
\[\frac{1}{4}\]
done
clear
E)
\[\frac{1}{2}\]
done
clear
View Answer play_arrow
question_answer 205) If the root of the equation\[\frac{a}{x-a}+\frac{b}{x-b}=1\]are equal in magnitude and opposite in sign, then:
A)
\[a=b\]
done
clear
B)
\[a+b=1\]
done
clear
C)
\[a-b=1\]
done
clear
D)
\[a+b=0\]
done
clear
E)
\[a+b=2\]
done
clear
View Answer play_arrow
question_answer 206) The equation of smallest degree with real coefficients having\[2+3i\]as one of the roots, is:
A)
\[{{x}^{2}}+4x+13=0\]
done
clear
B)
\[{{x}^{2}}+4x-13=0\]
done
clear
C)
\[{{x}^{2}}-4x+13=0\]
done
clear
D)
\[{{x}^{2}}-4x-13=0\]
done
clear
E)
\[{{x}^{2}}+2x+13=0\]
done
clear
View Answer play_arrow
question_answer 207) If the expression \[a(b-c){{x}^{2}}+b(c-a)xy+c(a-b){{y}^{2}}\]is a perfect square, then a, b, c are in:
A)
AP
done
clear
B)
HP
done
clear
C)
GP
done
clear
D)
both AP and GP
done
clear
E)
none of these
done
clear
View Answer play_arrow
question_answer 208) The value of n for which the expression\[\frac{{{x}^{n+1}}+{{y}^{n+1}}}{{{x}^{n}}+{{y}^{n}}}\]is arithmetic mean between\[x\]and y, is:
A)
0
done
clear
B)
1
done
clear
C)
\[-1\]
done
clear
D)
2
done
clear
E)
none of these
done
clear
View Answer play_arrow
question_answer 209) The angles A, B, C of a triangle ABC are in AP and sides b and c are in the ratio\[\sqrt{3}:\sqrt{2},\]then the angle A is:
A)
\[105{}^\circ \]
done
clear
B)
\[60{}^\circ \]
done
clear
C)
\[45{}^\circ \]
done
clear
D)
\[75{}^\circ \]
done
clear
E)
\[90{}^\circ \]
done
clear
View Answer play_arrow
question_answer 210) The sum of the series \[1+2.2+{{3.2}^{2}}+{{4.2}^{3}}+{{5.2}^{4}}+...+{{100.2}^{99}}\]is:
A)
\[{{99.2}^{100}}\]
done
clear
B)
\[{{100.2}^{100}}\]
done
clear
C)
\[{{99.2}^{100}}+1\]
done
clear
D)
\[{{1000.2}^{100}}\]
done
clear
E)
\[{{100.2}^{100}}-1\]
done
clear
View Answer play_arrow
question_answer 211) The sum to n terms of the series \[\frac{1}{2}+\frac{3}{4}+\frac{7}{8}+\frac{15}{16}+...\]is:
A)
\[{{2}^{n}}-1\]
done
clear
B)
\[1-{{2}^{n}}\]
done
clear
C)
\[n+{{2}^{n}}-1\]
done
clear
D)
\[n-1+{{2}^{-n}}\]
done
clear
E)
\[n-{{2}^{n}}-1\]
done
clear
View Answer play_arrow
question_answer 212) If A, G, H denotes respectively the AM, GM and HM between two unequal positive numbers, then:
A)
\[A={{G}^{2}}H\]
done
clear
B)
\[{{G}^{2}}=AH\]
done
clear
C)
\[{{A}^{2}}=GH\]
done
clear
D)
\[A=GH\]
done
clear
E)
none of these
done
clear
View Answer play_arrow
question_answer 213) If\[^{n}{{p}_{r}}={{720}^{n}}{{C}_{r}},\]then r is equal to:
A)
6
done
clear
B)
5
done
clear
C)
4
done
clear
D)
7
done
clear
E)
3
done
clear
View Answer play_arrow
question_answer 214) Everybody in a room shakes hands with everybody else. The total number of handshakes is 66. The number of persons in the room is:
A)
11
done
clear
B)
12
done
clear
C)
13
done
clear
D)
14
done
clear
E)
15
done
clear
View Answer play_arrow
question_answer 215) The number of four digit even numbers that can be formed using 0, 1, 2, 3, 4, 5, 6 without repetition, is:
A)
120
done
clear
B)
300
done
clear
C)
420
done
clear
D)
20
done
clear
E)
42
done
clear
View Answer play_arrow
question_answer 216) The number of circular permutations of n different objects is:
A)
\[n!\]
done
clear
B)
\[n\]
done
clear
C)
\[(n-2)!\]
done
clear
D)
\[(n-1)!\]
done
clear
E)
\[{{n}^{2}}\]
done
clear
View Answer play_arrow
question_answer 217) The coefficient of\[{{x}^{-9}}\]in the expansion of \[{{\left( \frac{{{x}^{2}}}{2}+\frac{2}{x} \right)}^{9}}\]is:
A)
512
done
clear
B)
\[-512\]
done
clear
C)
521
done
clear
D)
251
done
clear
E)
522
done
clear
View Answer play_arrow
question_answer 218) If the coefficients of the r th term and the \[(r+1)th\]term in the expansion of\[{{(1+x)}^{20}}\]are in the ratio\[1:2,\]then r is equal to:
A)
6
done
clear
B)
7
done
clear
C)
8
done
clear
D)
9
done
clear
E)
5
done
clear
View Answer play_arrow
question_answer 219) The number of ways in which 21 objects can be grouped into three groups of 8, 7 and 6 objects, is:
A)
\[\frac{20!}{8!+7!+6!}\]
done
clear
B)
\[\frac{21!}{8!7!}\]
done
clear
C)
\[\frac{21!}{8!7!6!}\]
done
clear
D)
\[\frac{21!}{8!+7!+6!}\]
done
clear
E)
none of these
done
clear
View Answer play_arrow
question_answer 220) The value of \[\left| \begin{matrix} {{1}^{2}} & {{2}^{2}} & {{3}^{2}} \\ {{2}^{2}} & {{3}^{2}} & {{4}^{2}} \\ {{3}^{2}} & {{4}^{2}} & {{5}^{2}} \\ \end{matrix} \right|\]is:
A)
8
done
clear
B)
\[-8\]
done
clear
C)
400
done
clear
D)
1
done
clear
E)
0
done
clear
View Answer play_arrow
question_answer 221) If\[A=\left[ \begin{matrix} 1 & 2 \\ 0 & 1 \\ \end{matrix} \right],\]then\[{{A}^{n}}\]is equal to:
A)
\[\left[ \begin{matrix} 1 & 2n \\ 0 & 1 \\ \end{matrix} \right]\]
done
clear
B)
\[\left[ \begin{matrix} 2 & n \\ 0 & 1 \\ \end{matrix} \right]\]
done
clear
C)
\[\left[ \begin{matrix} 1 & n \\ 0 & -1 \\ \end{matrix} \right]\]
done
clear
D)
\[\left[ \begin{matrix} 1 & n \\ 0 & 1 \\ \end{matrix} \right]\]
done
clear
E)
\[\left[ \begin{matrix} 1 & 2 \\ 0 & 1 \\ \end{matrix} \right]\]
done
clear
View Answer play_arrow
question_answer 222) If\[{{A}^{2}}-A+I=0,\]then the inverse of A is:
A)
\[{{A}^{-2}}\]
done
clear
B)
\[A+I\]
done
clear
C)
\[I-A\]
done
clear
D)
\[A-I\]
done
clear
E)
\[A\]
done
clear
View Answer play_arrow
question_answer 223) If\[\left[ \begin{matrix} 2+x & 3 & 4 \\ 1 & -1 & 2 \\ x & 1 & -5 \\ \end{matrix} \right]\]is a singular matrix, then\[x\]is:
A)
\[\frac{13}{25}\]
done
clear
B)
\[-\frac{25}{13}\]
done
clear
C)
\[\frac{5}{13}\]
done
clear
D)
\[\frac{25}{13}\]
done
clear
E)
\[-\frac{13}{25}\]
done
clear
View Answer play_arrow
question_answer 224) If A and B are square matrices of order 3 such that\[|A|-1,|B|=3,\]then the determinant value of the matrix 3AB is equal to:
A)
\[-9\]
done
clear
B)
\[-27\]
done
clear
C)
\[-81\]
done
clear
D)
81
done
clear
E)
9
done
clear
View Answer play_arrow
question_answer 225) If value of\[\left| \begin{matrix} a & a+b & a+2b \\ a+2b & a & a+b \\ a+b & a+2b & a \\ \end{matrix} \right|\]is equal to:
A)
\[9{{a}^{2}}(a+b)\]
done
clear
B)
\[9{{b}^{2}}(a+b)\]
done
clear
C)
\[{{a}^{2}}(a+b)\]
done
clear
D)
\[{{b}^{2}}(a+b)\]
done
clear
E)
\[9{{b}^{2}}(a-b)\]
done
clear
View Answer play_arrow
question_answer 226) For the matrix\[A=\left[ \begin{matrix} 1 & 1 & 0 \\ 1 & 2 & 1 \\ 2 & 1 & 0 \\ \end{matrix} \right]\]which is correct?
A)
\[{{A}^{3}}+3{{A}^{2}}-I=0\]
done
clear
B)
\[{{A}^{3}}-3{{A}^{2}}-I=0\]
done
clear
C)
\[{{A}^{3}}+2{{A}^{2}}-I=0\]
done
clear
D)
\[{{A}^{3}}-{{A}^{2}}+I=0\]
done
clear
E)
\[{{A}^{3}}+{{A}^{2}}-I=0\]
done
clear
View Answer play_arrow
question_answer 227) If\[\overrightarrow{a},\overrightarrow{b},\overrightarrow{c}\]are any three mutually perpendicular vectors of equal magnitude a, then\[|\overrightarrow{a}+\overrightarrow{b}+\overrightarrow{c}|\]:
A)
\[a\]
done
clear
B)
\[\sqrt{2}a\]
done
clear
C)
\[\sqrt{3}a\]
done
clear
D)
\[2\,a\]
done
clear
E)
none of these
done
clear
View Answer play_arrow
question_answer 228) If\[\overrightarrow{x}\]and\[\overrightarrow{y}\]are two unit vectors and\[\theta \]is the angle between them, then \[|\vec{x}-\vec{y}|\] is equal to:
A)
\[2\sin \left( \frac{\theta }{2} \right)\]
done
clear
B)
\[2\cos \left( \frac{\theta }{2} \right)\]
done
clear
C)
\[\sin \left( \frac{\theta }{2} \right)\]
done
clear
D)
\[\cos \left( \frac{\theta }{2} \right)\]
done
clear
E)
\[\left( \frac{\theta }{2} \right)\]
done
clear
View Answer play_arrow
question_answer 229) If\[\overrightarrow{a}=(2,-3,-7),\overrightarrow{b}=(3,-1,2),\]\[\overrightarrow{c}=(4,5,-1),\]then the scalar triple product\[[\overrightarrow{a}\text{ }\overrightarrow{b}\text{ }\overrightarrow{c}]\]is equal to:
A)
180
done
clear
B)
184
done
clear
C)
\[-184\]
done
clear
D)
84
done
clear
E)
none of these
done
clear
View Answer play_arrow
question_answer 230) The value of\[\overrightarrow{a}.\{(\overrightarrow{b}\times \overrightarrow{c})\times (\overrightarrow{a}+\overrightarrow{b}+\overrightarrow{c})\}\]is equal to:
A)
\[0\]
done
clear
B)
\[[\overrightarrow{a}\,\,\overrightarrow{b}\,\,\overrightarrow{c}]\]
done
clear
C)
\[2\overrightarrow{a}\]
done
clear
D)
\[\overrightarrow{a}\]
done
clear
E)
none of these
done
clear
View Answer play_arrow
question_answer 231) If\[|\overrightarrow{a}|=6,|\overrightarrow{b}|=8,|\overrightarrow{a}-\overrightarrow{b}|=10,\]then\[|a+b|\]is equal to:
A)
10
done
clear
B)
24
done
clear
C)
40
done
clear
D)
36
done
clear
E)
20
done
clear
View Answer play_arrow
question_answer 232) If\[|\overrightarrow{a}|=3,|\overrightarrow{b}|=5,|\overrightarrow{c}|=7,\]and\[\overrightarrow{a}+\overrightarrow{b}+\overrightarrow{c}=0,\]then the angle between\[\overrightarrow{a}\]and\[\overrightarrow{b}\]:
A)
\[15{}^\circ \]
done
clear
B)
\[{{\cos }^{-1}}\left( \frac{2}{3} \right)\]
done
clear
C)
\[30{}^\circ \]
done
clear
D)
\[60{}^\circ \]
done
clear
E)
\[90{}^\circ \]
done
clear
View Answer play_arrow
question_answer 233) The area of a parallelogram with diagonals as \[\overrightarrow{a}=3\hat{i}+\hat{j}-2\hat{k}\] and\[\overrightarrow{b}=\hat{i}-3\text{ }\hat{j}+4\text{ }\hat{k}\]is:
A)
\[10\sqrt{3}\]
done
clear
B)
\[\frac{10}{\sqrt{3}}\]
done
clear
C)
\[5\sqrt{3}\]
done
clear
D)
\[\frac{5}{\sqrt{3}}\]
done
clear
E)
\[\sqrt{3}\]
done
clear
View Answer play_arrow
question_answer 234) The position vectors of A, B and C are (1,1,1), \[(1,5,-1)\]and (2, 3, 5), then the greatest angle of the triangle is:
A)
\[135{}^\circ \]
done
clear
B)
\[90{}^\circ \]
done
clear
C)
\[{{\cos }^{-1}}\left( \frac{2}{3} \right)\]
done
clear
D)
\[{{\cos }^{-1}}\left( \frac{5}{7} \right)\]
done
clear
E)
\[105{}^\circ \]
done
clear
View Answer play_arrow
question_answer 235) If\[\overrightarrow{a}\]is a unit vector perpendicular to\[\overrightarrow{b}\]and\[\overrightarrow{c}\], the second unit vector perpendicular to\[\overrightarrow{b}\]and\[\overrightarrow{c}\] is:
A)
\[\overrightarrow{b}\times \overrightarrow{c}\]
done
clear
B)
\[\overrightarrow{a}\times \overrightarrow{b}\]
done
clear
C)
\[\overrightarrow{c}\]
done
clear
D)
\[\overrightarrow{a}\times \overrightarrow{c}\]
done
clear
E)
none of these
done
clear
View Answer play_arrow
question_answer 236) If\[\overrightarrow{a}.\hat{i}=\overrightarrow{a}.(\hat{i}+\hat{j}+\hat{k})=1,\]then\[\overrightarrow{a}\]is equal to:
A)
\[\hat{i}\]
done
clear
B)
\[\hat{j}\]
done
clear
C)
\[\hat{k}\]
done
clear
D)
\[\hat{i}+\hat{j}\]
done
clear
E)
none of these
done
clear
View Answer play_arrow
question_answer 237) If\[\theta \]is the angle between the planes \[2x-y+2z=3,\text{ }6x-2y+3z=5,\]then\[\cos \theta \]is equal to:
A)
\[\frac{21}{20}\]
done
clear
B)
\[\frac{11}{21}\]
done
clear
C)
\[\frac{20}{21}\]
done
clear
D)
\[\frac{12}{23}\]
done
clear
E)
\[\frac{23}{12}\]
done
clear
View Answer play_arrow
question_answer 238) The direction cosines of the normal to the plane\[6x-3y-2z=1\]are:
A)
\[\left( \frac{6}{7},3,\frac{-2}{7} \right)\]
done
clear
B)
\[(6,-3,-2)\]
done
clear
C)
\[\frac{1}{7}(6,-3,-2)\]
done
clear
D)
\[\frac{1}{7}(6,3,2)\]
done
clear
E)
\[\frac{1}{7}(-6,2,3)\]
done
clear
View Answer play_arrow
question_answer 239) If\[\alpha ,\beta ,\gamma \]are the angles made by a straight line with the co-ordinate axes, then \[si{{n}^{2}}\alpha +si{{n}^{2}}\beta \text{+ }si{{n}^{2}}\gamma \] is equal to:
A)
0
done
clear
B)
1
done
clear
C)
2
done
clear
D)
\[\frac{3}{2}\]
done
clear
E)
\[\frac{2}{3}\]
done
clear
View Answer play_arrow
question_answer 240) The equation of the plane through the intersection of the planes\[x+2y+3z-4=0\] and\[4x+3y+2z+1=0\]and passing through the origin, is:
A)
\[17x+14y+11z=0\]
done
clear
B)
\[7x+14y+11z=0\]
done
clear
C)
\[x+14y+11z=0\]
done
clear
D)
\[x+y+11z=0\]
done
clear
E)
\[17x+y+z=0\]
done
clear
View Answer play_arrow