question_answer 1) Two resistors of resistances\[200\,k\Omega \]and\[1\,M\Omega \] respectively form a potential divider with outer junctions maintained at potentials of\[+3V\]and\[-15V\]. Then, the potential at the junction between the resistors is
A)
\[+1\text{ }V\]
done
clear
B)
\[-0.6\text{ }V\]
done
clear
C)
zero
done
clear
D)
\[-\,12V\]
done
clear
E)
\[+12\text{ }V\]
done
clear
View Answer play_arrow
question_answer 2) The graph between resistivity and temperature, for a limited range of temperatures, is a straight line for a material like
A)
copper
done
clear
B)
nichrome
done
clear
C)
silicon
done
clear
D)
mercury
done
clear
E)
gallium arsenide
done
clear
View Answer play_arrow
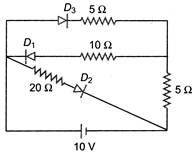
question_answer 3)
In the circuit shown, the current through the\[5\,\Omega \]resistor is
A)
\[\frac{8}{3}A\]
done
clear
B)
\[\frac{9}{13}A\]
done
clear
C)
\[\frac{4}{13}A\]
done
clear
D)
\[\frac{1}{3}A\]
done
clear
E)
\[\frac{2}{3}A\]
done
clear
View Answer play_arrow
question_answer 4) A solenoid has core of a material with relative permeability 500 and its windings carry a current of 1 A. The number of turns of the solenoid is \[500\text{ }{{m}^{-1}}\]. The magnetization of the material is nearly
A)
\[2.5\times {{10}^{3}}A{{m}^{-1}}\]
done
clear
B)
\[2.5\times {{10}^{5}}A{{m}^{-1}}\]
done
clear
C)
\[2.0\times {{10}^{3}}A{{m}^{-1}}\]
done
clear
D)
\[2.0\times {{10}^{5}}A{{m}^{-1}}\]
done
clear
E)
\[5\times {{10}^{5}}A{{m}^{-1}}\]
done
clear
View Answer play_arrow
question_answer 5) Choose the correct statement
A)
A paramagnetic material tends to move from a strong magnetic field to weak magnetic field
done
clear
B)
A magnetic material is in the paramagnetic phase below its Curie temperature
done
clear
C)
The resultant magnetic moment in an atom of a diamagnetic substance is zero
done
clear
D)
Typical domain size of a ferromagnetic material is 1 nm
done
clear
E)
The susceptibility of a ferromagnetic material is slightly greater than 1
done
clear
View Answer play_arrow
question_answer 6) A\[2\mu C\]charge moving around a circle with a frequency of\[6.25\times {{10}^{12}}Hz\] produces a magnetic field 6.28 T at the centre of the circle. The radius of the circle is
A)
2.25m
done
clear
B)
0.25m
done
clear
C)
13.0m
done
clear
D)
1.25m
done
clear
E)
3.25m
done
clear
View Answer play_arrow
question_answer 7) A galvanometer of resistance \[100\,\,\Omega \] is converted to a voltmeter of range 10 V by connecting a resistance of\[10\,k\Omega \]. The resistance required to convert the same galvanometer to an ammeter of range 1 A is
A)
\[0.4\,\Omega \]
done
clear
B)
\[0.3\,\,\Omega \]
done
clear
C)
\[1.2\,\Omega \]
done
clear
D)
\[0.2\,\,\Omega \]
done
clear
E)
\[0.1\,\Omega \]
done
clear
View Answer play_arrow
question_answer 8)
Two wires with currents 2A and 1A are enclosed in a circular loop. Another wire with current 3 A is situated outside the loop as shown. Then\[\oint{\overrightarrow{B}}.\overrightarrow{dl}\]around the loop is
A)
\[{{\mu }_{0}}\]
done
clear
B)
\[3{{\mu }_{0}}\]
done
clear
C)
\[6{{\mu }_{0}}\]
done
clear
D)
\[2{{\mu }_{0}}\]
done
clear
E)
zero
done
clear
View Answer play_arrow
question_answer 9) An L-C-R series AC circuit is at resonance with 10 V each across L, C and R. If the resistance is halved, the respective voltages across L, C and R are
A)
10 V, 10 V and 5 V
done
clear
B)
10 V, 10 V and 10 V
done
clear
C)
20V, 20V and 5V
done
clear
D)
20 V, 20 V and 10 V
done
clear
E)
5 V, 5 V and 5 V
done
clear
View Answer play_arrow
question_answer 10) A 50 Hz AC current of peak value 2 A flows through one of the pair of coils. If the mutual inductance between the pair of coils is 150 mH, then the peak value of voltage induced in the second coil is
A)
\[30\,\pi V\]
done
clear
B)
\[60\,\pi V\]
done
clear
C)
\[15\,\pi V\]
done
clear
D)
\[300\,\pi V\]
done
clear
E)
\[3\,\pi V\]
done
clear
View Answer play_arrow
question_answer 11) A transformer is used to light a 100 W and 110 V lamp from a 220 V main supply. If the main current is 0.5 A, then the efficiency of the transformer is nearly
A)
89%
done
clear
B)
100%
done
clear
C)
95%
done
clear
D)
85%
done
clear
E)
91%
done
clear
View Answer play_arrow
question_answer 12) An L-C-R series circuit is at resonance. Then
A)
the phase difference between current and voltage is\[{{90}^{o}}\]
done
clear
B)
the phase difference between current and voltage is\[{{45}^{o}}\]
done
clear
C)
its impedance is purely resistive
done
clear
D)
its impedance is zero
done
clear
E)
the current is minimum
done
clear
View Answer play_arrow
question_answer 13) A 100 W bulb produces an electric field of \[2.9\text{ }V{{m}^{-1}}\]at a point 3 m away. If the bulb is replaced by 400 W bulb without distributing other conditions, then the electric field produced at the same point is
A)
\[2.9\text{ }V{{m}^{-1}}\]
done
clear
B)
\[3.5\text{ }V{{m}^{-1}}\]
done
clear
C)
\[5\text{ }V{{m}^{-1}}\]
done
clear
D)
\[5.8\text{ }V{{m}^{-1}}\]
done
clear
E)
\[\text{1}\text{.45 }V{{m}^{-1}}\]
done
clear
View Answer play_arrow
question_answer 14) In the total electromagnetic energy falling on a surface is U, then the total momentum delivered (for complete absorption) is
A)
\[\frac{U}{c}\]
done
clear
B)
\[cU\]
done
clear
C)
\[\frac{U}{{{c}^{2}}}\]
done
clear
D)
\[{{c}^{2}}U\]
done
clear
E)
\[\sqrt{\frac{U}{c}}\]
done
clear
View Answer play_arrow
question_answer 15) The focal lengths of the objective and of the eye-piece of a compound microscope are\[{{f}_{o}}\]and\[{{f}_{e}}\]respectively. If L is the tube length and D, the least distance of distinct vision, then its angular magnification, when the image is formed at infinity, is
A)
\[\left( 1-\frac{L}{{{f}_{o}}} \right)\left( \frac{D}{{{f}_{e}}} \right)\]
done
clear
B)
\[\left( 1+\frac{L}{{{f}_{o}}} \right)\left( \frac{D}{{{f}_{e}}} \right)\]
done
clear
C)
\[\frac{L}{{{f}_{o}}}\left( 1-\frac{D}{{{f}_{e}}} \right)\]
done
clear
D)
\[\frac{L}{{{f}_{o}}}\left( 1+\frac{D}{{{f}_{e}}} \right)\]
done
clear
E)
\[\frac{L}{{{f}_{o}}}\left( \frac{D}{{{f}_{e}}} \right)\]
done
clear
View Answer play_arrow
question_answer 16) The velocity of a moving galaxy is\[300\text{ }km{{s}^{-1}}\] and the apparent change in wavelength of a spectral line emitted from the galaxy is observed as 0.5 nm. Then, the actual wavelength of the spectral line is
A)
\[3000\,\overset{\text{o}}{\mathop{\text{A}}}\,\]
done
clear
B)
\[5000\,\overset{\text{o}}{\mathop{\text{A}}}\,\]
done
clear
C)
\[6000\,\overset{\text{o}}{\mathop{\text{A}}}\,\]
done
clear
D)
\[4500\,\overset{\text{o}}{\mathop{\text{A}}}\,\]
done
clear
E)
\[5500\,\overset{\text{o}}{\mathop{\text{A}}}\,\]
done
clear
View Answer play_arrow
question_answer 17) An astronomical telescope has an angular magnification of magnitude 5 for distant objects. The separation between the objective and the eye-piece is 36 cm and the final image is formed at infinity. The focal length\[{{f}_{o}}\]of the objective and\[{{f}_{e}}\]of the eye-piece are respectively
A)
45 cm and 9 cm
done
clear
B)
50 cm and 10 cm
done
clear
C)
7.2 cm and 5 cm
done
clear
D)
30 cm and 6 cm
done
clear
E)
5 cm and 7.2 cm
done
clear
View Answer play_arrow
question_answer 18) If the reflected image formed is magnified and virtual, then the mirror system is
A)
concave only
done
clear
B)
convex only
done
clear
C)
plane
done
clear
D)
concave or convex
done
clear
E)
convex or plane
done
clear
View Answer play_arrow
question_answer 19) A vessel of depth x is half filled with oil of refractive index \[{{\mu }_{1}}\] and the other half is filled with water of refractive index\[{{\mu }_{2}}\]The apparent depth of the vessel when viewed from above is
A)
\[\frac{x({{\mu }_{1}}+{{\mu }_{2}})}{2{{\mu }_{1}}{{\mu }_{2}}}\]
done
clear
B)
\[\frac{x\,{{\mu }_{1}}\,{{\mu }_{2}}}{2({{\mu }_{1}}+{{\mu }_{2}})}\]
done
clear
C)
\[\frac{x{{\mu }_{1}}{{\mu }_{2}}}{({{\mu }_{1}}+{{\mu }_{2}})}\]
done
clear
D)
\[\frac{2x({{\mu }_{1}}+{{\mu }_{2}})}{{{\mu }_{1}}{{\mu }_{2}}}\]
done
clear
E)
\[\frac{4({{\mu }_{1}}+{{\mu }_{2}})x}{{{\mu }_{1}}{{\mu }_{2}}}\]
done
clear
View Answer play_arrow
question_answer 20) If m is the mass of an electron and c is the speed of light, the ratio of the wavelength of a photon of energy E to that of the electron of the same energy is
A)
\[c\sqrt{\frac{2m}{E}}\]
done
clear
B)
\[\sqrt{\frac{2m}{E}}\]
done
clear
C)
\[\sqrt{\frac{2m}{cE}}\]
done
clear
D)
\[\sqrt{\frac{m}{E}}\]
done
clear
E)
\[\sqrt{\frac{cm}{E}}\]
done
clear
View Answer play_arrow
question_answer 21) The set which represents the isotope, isobar and isotone respectively is
A)
\[{{(}_{1}}{{H}^{2}}{{,}_{1}}{{H}^{3}}),{{(}_{79}}A{{u}^{197}}{{,}_{80}}H{{g}^{198}})\]and\[{{(}_{2}}H{{e}^{3}}{{,}_{1}}{{H}^{2}})\]
done
clear
B)
\[{{(}_{2}}H{{e}^{3}}{{,}_{1}}{{H}^{2}}),{{(}_{79}}A{{u}^{197}}{{,}_{80}}H{{g}^{198}})\]and\[{{(}_{1}}{{H}^{1}}{{,}_{1}}{{H}^{3}})\]
done
clear
C)
\[{{(}_{2}}H{{e}^{3}}{{,}_{1}}{{H}^{3}}),{{(}_{1}}{{H}^{2}}{{,}_{1}}{{H}^{3}})\]and\[{{(}_{79}}A{{u}^{197}}{{,}_{80}}H{{g}^{198}})\]
done
clear
D)
\[{{(}_{1}}{{H}^{2}}{{,}_{1}}{{H}^{3}}),{{(}_{2}}H{{e}^{3}}{{,}_{1}}{{H}^{3}})\]and\[{{(}_{79}}A{{u}^{197}}{{,}_{80}}H{{g}^{198}})\]
done
clear
E)
\[{{(}_{1}}{{H}^{1}}{{,}_{1}}{{H}^{3}}),{{(}_{79}}A{{u}^{197}}{{,}_{80}}H{{g}^{198}})\]and\[{{(}_{2}}H{{e}^{3}}{{,}_{1}}{{H}^{3}})\]
done
clear
View Answer play_arrow
question_answer 22) Two samples X and Y contain equal amount of radioactive substances. If\[\frac{1}{16}\]th of the sample X and\[\frac{1}{256}\]th of the sample V, remain after 8 h, then the ratio of half periods of X and Y is
A)
2 : 1
done
clear
B)
1 : 2
done
clear
C)
1 : 4
done
clear
D)
1 : 16
done
clear
E)
4 : 1
done
clear
View Answer play_arrow
question_answer 23) Radioactive\[_{27}^{60}Co\]is transformed into stable\[_{28}^{60}Ni\]by emitting two\[\gamma -\]rays of energies
A)
1.33 MeV and 1.17 MeV in succession
done
clear
B)
1.17 MeV and 1.33 MeV in succession
done
clear
C)
1.37 MeV and 1.13 MeV in succession
done
clear
D)
1.13 MeV and 1.37 MeV in succession
done
clear
E)
1.17 MeV and 1.13 MeV in succession
done
clear
View Answer play_arrow
question_answer 24) A pure semiconductor has equal electron and hole concentration of\[{{10}^{16}}{{m}^{-3}}\]. Doping by indium increases\[{{n}_{h}}\]to\[5\times {{10}^{22}}{{m}^{-3}}\]. Then, the value of \[{{n}_{e}}\] in the doped semiconductor is
A)
\[{{10}^{6}}/{{m}^{3}}\]
done
clear
B)
\[{{10}^{22}}/{{m}^{3}}\]
done
clear
C)
\[2\times {{10}^{6}}/{{m}^{3}}\]
done
clear
D)
\[{{10}^{19}}/{{m}^{3}}\]
done
clear
E)
\[2\times {{10}^{9}}/{{m}^{3}}\]
done
clear
View Answer play_arrow
question_answer 25) The collector supply voltage is 6 V and the voltage drop across a resistor of\[600\,\Omega \]. in the collector circuit is 0.6 V, in a transistor connected in common emitter mode. If the current gain is 20, the base current is
A)
0.25mA
done
clear
B)
0.05mA
done
clear
C)
0.12mA
done
clear
D)
0.02mA
done
clear
E)
0.07mA
done
clear
View Answer play_arrow
question_answer 26)
A full-wave rectifier circuit with an AC input is shown
A)
done
clear
B)
done
clear
C)
done
clear
D)
done
clear
E)
done
clear
View Answer play_arrow
question_answer 27)
In the given circuit the current through the battery is
A)
0.5 A
done
clear
B)
1 A
done
clear
C)
1.5 A
done
clear
D)
2 A
done
clear
E)
2.5 A
done
clear
View Answer play_arrow
question_answer 28) A carrier frequency of 1 MHz and peak value of 10 V is amplitude modulated with a signal frequency of 10 kHz with peak value of 0.5 V. Then the modulation index and the side band frequencies respectively are
A)
0.05 and 1 ± 0.010 MHz
done
clear
B)
0.5 and 1 ± 0.010 MHz
done
clear
C)
0.05 and 1 ± 0.005 MHz
done
clear
D)
0.5 and 1 ± 0.005 MHz
done
clear
E)
0.05 and 1± 0.100 MHz
done
clear
View Answer play_arrow
question_answer 29) The maximum line-of-sight distance\[{{d}_{M}}\]between two antennas having heights\[{{h}_{t}}\]and\[{{h}_{R}}\]above the earth is
A)
\[\sqrt{R({{h}_{T}}+{{h}_{R}})}\]
done
clear
B)
\[\sqrt{2R/({{h}_{T}}+{{h}_{R}})}\]
done
clear
C)
\[\sqrt{R{{h}_{T}}}+\sqrt{2R{{h}_{R}}}\]
done
clear
D)
\[\sqrt{2R{{h}_{T}}}+\sqrt{2R{{h}_{R}}}\]
done
clear
E)
\[\sqrt{2R{{h}_{T}}}+\sqrt{R{{h}_{R}}}\]
done
clear
View Answer play_arrow
question_answer 30) The frequency band used in the downlink of satellite communication is
A)
9.5 to 2.5 GHz
done
clear
B)
896 to 901 MHz
done
clear
C)
3.7 to 4.2 GHz
done
clear
D)
840 to 935 MHz
done
clear
E)
3.7 to 4.2 MHz
done
clear
View Answer play_arrow
question_answer 31) In amplitude modulation, the bandwidth is
A)
twice the audio signal frequency
done
clear
B)
thrice the audio signal frequency
done
clear
C)
thrice the carrier wave frequency
done
clear
D)
twice the carrier wave frequency
done
clear
E)
sum of audio signal frequency and carrier wave frequency
done
clear
View Answer play_arrow
question_answer 32) The quantities RC and\[\left( \frac{L}{R} \right)\](where R, L and C stand for resistance, inductance and capacitance respectively) have the dimensions of
A)
force
done
clear
B)
linear momentum
done
clear
C)
linear acceleration
done
clear
D)
time
done
clear
E)
linear velocity
done
clear
View Answer play_arrow
question_answer 33) The number of significant figures in 0.002305 is
A)
6
done
clear
B)
4
done
clear
C)
7
done
clear
D)
2
done
clear
E)
3
done
clear
View Answer play_arrow
question_answer 34) A body travelling with uniform acceleration crosses two points A and B with velocities \[20\,m{{s}^{-1}}\] and \[30\,m{{s}^{-1}}\] respectively. The speed of the body at the mid-point of A and B is nearest to
A)
\[25.5\,m{{s}^{-1}}\]
done
clear
B)
\[25\,m{{s}^{-1}}\]
done
clear
C)
\[24\text{ }m{{s}^{-1}}\]
done
clear
D)
\[10\sqrt{6}\,m{{s}^{-1}}\]
done
clear
E)
\[22\,m{{s}^{-1}}\]
done
clear
View Answer play_arrow
question_answer 35) An aeroplane flies around a square field ABCD of each side 1000 km. Its speed along AB is \[250\text{ }km{{h}^{-1}},\]along BC\[500\text{ }km{{h}^{-1}},\] along CD \[200km{{h}^{-1}},\]and along DA \[100\text{ }km{{h}^{-1}}\]. Its average speed (in\[km{{h}^{-1}}\])over the entire trip is
A)
225.5
done
clear
B)
175.5
done
clear
C)
125.5
done
clear
D)
310.5
done
clear
E)
190.5
done
clear
View Answer play_arrow
question_answer 36) Free fall of an object (in vacuum) is a case of motion with
A)
uniform velocity
done
clear
B)
uniform acceleration
done
clear
C)
variable acceleration
done
clear
D)
constant momentum
done
clear
E)
uniform speed
done
clear
View Answer play_arrow
question_answer 37) The maximum height of a projectile is half of its range on the horizontal. If the velocity of projection is u, its range on the horizontal is
A)
\[\frac{2{{u}^{2}}}{5g}\]
done
clear
B)
\[\frac{3{{u}^{2}}}{5g}\]
done
clear
C)
\[\frac{{{u}^{2}}}{g}\]
done
clear
D)
\[\frac{{{u}^{2}}}{5g}\]
done
clear
E)
\[\frac{4{{u}^{2}}}{5g}\]
done
clear
View Answer play_arrow
question_answer 38) A stone of mass 2 kg is tied to a string of length 0.5 m. If the breaking tension of the string is 900 N, then the maximum angular velocity, the stone can have in uniform circular motion is
A)
\[30\,rad{{s}^{-1}}\]
done
clear
B)
\[20\,rad{{s}^{-1}}\]
done
clear
C)
\[10\,rad{{s}^{-1}}\]
done
clear
D)
\[25\,rad{{s}^{-1}}\]
done
clear
E)
\[40\,rad{{s}^{-1}}\]
done
clear
View Answer play_arrow
question_answer 39) The position of a particle is given by \[\overrightarrow{r}=2{{t}^{2}}\hat{i}+3t\hat{j}+4\hat{k},\]where t is in second and the coefficients have proper units for\[\overrightarrow{r}\]to be in metre. The\[\overrightarrow{a}(t)\]of the particle at\[t=1\text{ }s\] is
A)
\[4\text{ }m{{s}^{-2}}\]along \[\text{y-}\]direction
done
clear
B)
\[\text{3 }m{{s}^{-2}}\]along\[x\text{-}\]direction
done
clear
C)
\[4\text{ }m{{s}^{-2}}\]along\[x\text{-}\]direction
done
clear
D)
\[\text{2 }m{{s}^{-2}}\]along\[\text{z-}\]direction
done
clear
E)
\[\text{3 }m{{s}^{-2}}\]along\[\text{z-}\]direction
done
clear
View Answer play_arrow
question_answer 40) A passenger getting down from a moving bus, falls in the direction of the motion of the bus. This is an example for
A)
moment of inertia
done
clear
B)
second law of motion
done
clear
C)
third law of motion
done
clear
D)
inertia of rest
done
clear
E)
inertia of motion
done
clear
View Answer play_arrow
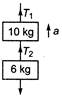
question_answer 41)
A body of mass 6 kg is hanging from another body of mass 10 kg as shown in figure. This combination is being pulled up by a string with an acceleration of\[2\text{ }m{{s}^{-2}}\]. The tension\[{{T}_{1}}\]is \[(g=10\text{ }m{{s}^{-2}})\]
A)
240 N
done
clear
B)
150 N
done
clear
C)
220 N
done
clear
D)
192 N
done
clear
E)
178N
done
clear
View Answer play_arrow
question_answer 42) Which one of the following is not a contact force?
A)
Viscous force
done
clear
B)
Air resistance
done
clear
C)
Friction
done
clear
D)
Buoyant force
done
clear
E)
Magnetic force
done
clear
View Answer play_arrow
question_answer 43) A force\[(4\hat{i}+\hat{j}-2\hat{k})N\]acting on a body maintains its velocity at\[(2\hat{i}+2\hat{j}+3\hat{k})m{{s}^{-1}}\]. The power exerted is
A)
4W
done
clear
B)
5W
done
clear
C)
2W
done
clear
D)
8W
done
clear
E)
1W
done
clear
View Answer play_arrow
question_answer 44) Energy required to break one bond in DNA is
A)
\[{{10}^{-10}}J\]
done
clear
B)
\[{{10}^{-18}}J\]
done
clear
C)
\[{{10}^{-7}}J\]
done
clear
D)
\[{{10}^{-20}}J\]
done
clear
E)
\[{{10}^{-3}}J\]
done
clear
View Answer play_arrow
question_answer 45) Identify the false statement from the following
A)
Work-energy theorem is not independent of Newtons second law
done
clear
B)
Work-energy theorem holds in all inertial frames
done
clear
C)
Work done by friction over a closed path is zero
done
clear
D)
No potential energy can be associated with friction
done
clear
E)
Work done is a scalar quantity
done
clear
View Answer play_arrow
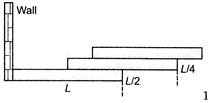
question_answer 46)
Three bricks each of length L and mass M are arranged as shown from the wall. The distance of the centre of mass of the system from the wall is
A)
\[L/4\]
done
clear
B)
\[L/2\]
done
clear
C)
\[(3/2)L\]
done
clear
D)
\[(11/12)L\]
done
clear
E)
\[(5/6)L\]
done
clear
View Answer play_arrow
question_answer 47) A fly wheel of moment of inertia\[3\times {{10}^{2}}kg\text{ }{{m}^{2}}\]is rotating with uniform angular speed of 4.6 \[rad{{s}^{-1}}\]. If a torque of\[6.9\times {{10}^{2}}Nm\]retards the wheel, then the time in which the wheel comes to rest is
A)
1.5 s
done
clear
B)
2 s
done
clear
C)
0.5 s
done
clear
D)
1 s
done
clear
E)
2.5 s
done
clear
View Answer play_arrow
question_answer 48) Moment of inertia of a ring of mass M and radius R about a tangent to the circle of the ring is
A)
\[\frac{5}{2}M{{R}^{2}}\]
done
clear
B)
\[\frac{3}{2}M{{R}^{2}}\]
done
clear
C)
\[\frac{1}{2}M{{R}^{2}}\]
done
clear
D)
\[M{{R}^{2}}\]
done
clear
E)
\[\frac{7}{2}M{{R}^{2}}\]
done
clear
View Answer play_arrow
question_answer 49) If the escape velocity of a planet is 3 times that of the earth and its radius is 4 times that of the earth, then the mass of the planet is (Mass of the earth\[=6\times {{10}^{24}}kg\])
A)
\[1.62\times {{10}^{22}}kg\]
done
clear
B)
\[0.72\times {{10}^{22}}kg\]
done
clear
C)
\[2.16\times {{10}^{26}}kg\]
done
clear
D)
\[1.22\times {{10}^{22}}kg\]
done
clear
E)
\[3.6\times {{10}^{22}}kg\]
done
clear
View Answer play_arrow
question_answer 50) The total energy of a circularly orbiting satellite is
A)
twice the kinetic energy of the satellite
done
clear
B)
half the kinetic energy of the satellite
done
clear
C)
twice the potential energy of the satellite
done
clear
D)
equal to the potential energy of the satellite
done
clear
E)
half the potential energy of the satellite
done
clear
View Answer play_arrow
question_answer 51) If an earth satellite of mass m orbiting at a distance 2 R from the centre of earth has to be transferred into the orbit of radius 3 R, the amount of energy required is (R = radius of earth)
A)
\[mgR\]
done
clear
B)
\[\frac{mgR}{3}\]
done
clear
C)
\[\frac{mgR}{2}\]
done
clear
D)
\[\frac{mgR}{12}\]
done
clear
E)
\[\frac{mgR}{9}\]
done
clear
View Answer play_arrow
question_answer 52) The compressibility of water is \[6\times {{10}^{-10}}{{N}^{-1}}{{m}^{2}}\]. If one litre is subjected to a pressure of \[4\times {{10}^{7}}N{{m}^{-2}},\]the decrease in its volume is
A)
2.4 cc
done
clear
B)
10 cc
done
clear
C)
24 cc
done
clear
D)
15 cc
done
clear
E)
12 cc
done
clear
View Answer play_arrow
question_answer 53) Bernoullis principle is not involved in the working/explanation of
A)
movement of spinning ball
done
clear
B)
carburettes of automobile
done
clear
C)
blades of a kitchen mixer
done
clear
D)
heart attack
done
clear
E)
dynamic lift of an aeroplane
done
clear
View Answer play_arrow
question_answer 54) Which one of the following statements is correct? In the case of
A)
shearing stress there is change in volume
done
clear
B)
tensile stress there is no change in volume
done
clear
C)
shearing stress there is no change in shape
done
clear
D)
hydraulic stress there is no change in volume
done
clear
E)
tensile stress there is no change in shape
done
clear
View Answer play_arrow
question_answer 55) The onset of turbulence in a liquid is determined by
A)
Pascals law
done
clear
B)
Magnus effect
done
clear
C)
Reynolds number
done
clear
D)
Bernoullis principle
done
clear
E)
Torricellis law
done
clear
View Answer play_arrow
question_answer 56) The temperature at which oxygen molecules have the same root mean square speed as that of hydrogen molecules at 300 K is
A)
600 K
done
clear
B)
2400 K
done
clear
C)
1200 K
done
clear
D)
300 K
done
clear
E)
4800 K
done
clear
View Answer play_arrow
question_answer 57) Mean free path of a gas molecule is
A)
inversely proportional to number of molecules per unit volume
done
clear
B)
inversely proportional to diameter of the molecule
done
clear
C)
directly proportional to the square root of the absolute temperature
done
clear
D)
directly proportional to the molecular mass
done
clear
E)
independent of temperature
done
clear
View Answer play_arrow
question_answer 58) A refrigerator with coefficient of performance \[\frac{1}{3}\]releases 200 J of heat to a hot reservoir. Then the work done on the working substance is
A)
\[\frac{100}{3}J\]
done
clear
B)
\[100J\]
done
clear
C)
\[\frac{200}{3}J\]
done
clear
D)
\[150J\]
done
clear
E)
\[50J\]
done
clear
View Answer play_arrow
question_answer 59) The heat capacity per mole of water is (R is universal gas constant)
A)
\[9R\]
done
clear
B)
\[\frac{9}{2}R\]
done
clear
C)
\[6R\]
done
clear
D)
\[5R\]
done
clear
E)
\[3R\]
done
clear
View Answer play_arrow
question_answer 60) If the frequency of human heart beat is 1.25 Hz, the number of heart beats in 1 min is
A)
80
done
clear
B)
65
done
clear
C)
90
done
clear
D)
75
done
clear
E)
120
done
clear
View Answer play_arrow
question_answer 61) A particle oscillating under a force\[\overrightarrow{F}=-k\overrightarrow{x}-b\overrightarrow{v}\] is a(/c and b are constants)
A)
simple harmonic oscillator
done
clear
B)
non linear oscillator
done
clear
C)
damped oscillator
done
clear
D)
forced oscillator
done
clear
E)
linear oscillator
done
clear
View Answer play_arrow
question_answer 62) A mass of 4 kg suspended from a spring of force constant\[800\text{ }N{{m}^{-1}}\]executes simple harmonic oscillations. If the total energy of the oscillator is 4 J, the maximum 1accelerations (in\[m{{s}^{-2}}\]) of the mass is
A)
5
done
clear
B)
15
done
clear
C)
45
done
clear
D)
20
done
clear
E)
25
done
clear
View Answer play_arrow
question_answer 63) The principle of superposition is basic to the phenomenon of
A)
total internal reflection
done
clear
B)
interference
done
clear
C)
reflection
done
clear
D)
refraction
done
clear
E)
polarization
done
clear
View Answer play_arrow
question_answer 64) Velocity of sound in air is\[320\text{ }m{{s}^{-1}}\]. A pipe closed at one end has a length of 1 m. Neglecting end correction, the air column in the pipe cannot resonate with sound of frequency
A)
80 Hz
done
clear
B)
240 Hz
done
clear
C)
320 Hz
done
clear
D)
400 Hz
done
clear
E)
560 Hz
done
clear
View Answer play_arrow
question_answer 65) A whistle is blown from the tower of a factory with a frequency of 220 Hz. The apparent frequency of sound heard by a worker moving towards the factory with a velocity of\[30\text{ }m{{s}^{-1}}\] is (velocity of sound\[=330\text{ }m{{s}^{-1}}\])
A)
280 Hz
done
clear
B)
200 Hz
done
clear
C)
300 Hz
done
clear
D)
240 Hz
done
clear
E)
330 Hz
done
clear
View Answer play_arrow
question_answer 66) n identical drops, each of capacitance C and charged to a potential V, coalesce to form a bigger drop. Then the ratio of the energy stored in the big drop to that in each small drop is
A)
\[{{n}^{5/3}}:1\]
done
clear
B)
\[{{n}^{4/3}}:1\]
done
clear
C)
\[n:1\]
done
clear
D)
\[{{n}^{3}}:1\]
done
clear
E)
\[{{n}^{2/3}}:1\]
done
clear
View Answer play_arrow
question_answer 67) Two charged spherical conductors of radii\[{{R}_{1}}\] and\[{{R}_{2}}\]are connected by a wire. Then the ratio of surface charge densities of the spheres\[{{\sigma }_{1}}/{{\sigma }_{2}}\]is
A)
\[{{R}_{1}}/{{R}_{2}}\]
done
clear
B)
\[{{R}_{2}}/{{R}_{1}}\]
done
clear
C)
\[\sqrt{({{R}_{1}}/{{R}_{2}})}\]
done
clear
D)
\[R_{1}^{2}/R_{2}^{2}\]
done
clear
E)
\[R_{2}^{2}/R_{1}^{2}\]
done
clear
View Answer play_arrow
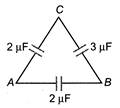
question_answer 68)
Three capacitors are connected in the arms of a triangle ABC as shown in figure. 5 V is applied between A and B. The voltage between B and C is
A)
2 V
done
clear
B)
1 V
done
clear
C)
3 V
done
clear
D)
1.5 V
done
clear
E)
0.5 V
done
clear
View Answer play_arrow
question_answer 69) Two point charges\[+5\mu C\]and\[-2\mu C\]are kept at a distance of 1 m in free space. The distance between the two zero potential points on the line joining the charges is
A)
\[\frac{2}{7}m\]
done
clear
B)
\[\frac{2}{3}m\]
done
clear
C)
\[\frac{22}{21}m\]
done
clear
D)
\[\frac{20}{21}m\]
done
clear
E)
\[\frac{8}{21}m\]
done
clear
View Answer play_arrow
question_answer 70) A negatively charged oil drop is prevented from falling under gravity by applying a vertical electric field\[100\text{ }V{{m}^{-1}}\]. If the mass of the drop is\[1.6\times {{10}^{-3}}g,\] the number of electrons carried by the drop is\[(g=10\text{ }in{{s}^{-2}})\]
A)
\[{{10}^{18}}\]
done
clear
B)
\[{{10}^{15}}\]
done
clear
C)
\[{{10}^{6}}\]
done
clear
D)
\[{{10}^{9}}\]
done
clear
E)
\[{{10}^{12}}\]
done
clear
View Answer play_arrow
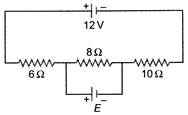
question_answer 71)
In the circuit shown, the current through\[8\,\Omega ,\]is same before and after connecting E. The value of E is
A)
12V
done
clear
B)
6V
done
clear
C)
4V
done
clear
D)
2V
done
clear
E)
8V
done
clear
View Answer play_arrow
question_answer 72) An electric bulb rated 500 W at 100 V is used in a circuit having a 200 V supply. The resistance R that must be put in series with the bulb, so that the bulb draws 500 W is
A)
\[10\,\Omega ,\]
done
clear
B)
\[15\,\Omega ,\]
done
clear
C)
\[2.5\,\Omega ,\]
done
clear
D)
\[25\,\Omega ,\]
done
clear
E)
\[20\,\Omega ,\]
done
clear
View Answer play_arrow
question_answer 73) The decreasing order of acidic character among ethane (I), ethene (II), ethyne (III) and propyne (IV) is
A)
(I) > (II) > (III) > (IV)
done
clear
B)
(II) > (III) > (I) > (IV)
done
clear
C)
(III) > (IV) > (II) > (I)
done
clear
D)
(IV) > (III) > (II) > (I)
done
clear
E)
(III) > (IV) > (I) > (II)
done
clear
View Answer play_arrow
question_answer 74) The alkene that will give the same product with HBr in the absence as well as in the presence of peroxide is
A)
2-butene
done
clear
B)
1-butene
done
clear
C)
propene
done
clear
D)
1-hexene
done
clear
E)
2-methylpropene
done
clear
View Answer play_arrow
question_answer 75) Hyperconjugation is most useful for stabilising which of the following carbocations?
A)
Neo-pentyl
done
clear
B)
Tert-butyl
done
clear
C)
\[Iso-\]propyl
done
clear
D)
Ethyl
done
clear
E)
Methyl
done
clear
View Answer play_arrow
question_answer 76) Choose the weakest acid among the following
A)
\[{{F}_{3}}CCOOH\]
done
clear
B)
\[F-C{{H}_{2}}COOH\]
done
clear
C)
\[C{{H}_{3}}COOH\]
done
clear
D)
\[C{{H}_{3}}C{{H}_{2}}COOH\]
done
clear
E)
\[{{(C{{H}_{3}})}_{2}}CH-COOH\]
done
clear
View Answer play_arrow
question_answer 77) The isomerism that arises due to restricted bond rotation is
A)
metamerism
done
clear
B)
optical isomerism
done
clear
C)
position isomerism
done
clear
D)
geometrical isomerism
done
clear
E)
functional isomerism
done
clear
View Answer play_arrow
question_answer 78) The IUPAC name of the following compound, \[[{{(C{{H}_{3}})}_{2}}CH-C{{H}_{2}}-CH=CH-CH=CH-\underset{\begin{smallmatrix} | \\ {{C}_{2}}{{H}_{5}} \end{smallmatrix}}{\mathop{CH}}\,-C{{H}_{3}}\]is
A)
1, 1, 7, 7-tetramethyl-2, 5-octadiene
done
clear
B)
2, 8-dimethyl-3, 6-decadiene
done
clear
C)
1, 5-diisopropyl-1, 4-hexadiene
done
clear
D)
3, 9-dimethyl-4, 6-decadiene
done
clear
E)
2, 8-dimethyl-4, 6-decadiene
done
clear
View Answer play_arrow
question_answer 79) Chlorination of benzene in the presence of halogen carrier is an example of
A)
aromatic nucleophilic substitution
done
clear
B)
aromatic electrophilic substitution
done
clear
C)
aromatic nucleophilic addition
done
clear
D)
aromatic electrophilic addition
done
clear
E)
free radical substitution
done
clear
View Answer play_arrow
question_answer 80)
Aryl halides doesnt undergo nucleophilic substitution reactions under ordinary conditions because of 1. approach of nucleophile is retarded 2. carbon carrying halogen atoms is\[s{{p}^{3}}-\]hybridised 3. the substrate molecule is destabilised due to resonance 4. partial double bond character between carbon and halogen
A)
2 and 4 only
done
clear
B)
1 and 4 only
done
clear
C)
2 and 3 only
done
clear
D)
2, 3 and 4 only
done
clear
E)
1 and 3 only
done
clear
View Answer play_arrow
question_answer 81)
Aldehydes that do not undergo aldol condensation are 1. propanal 2. trichloroethanal 3. methanal 4. ethanal 5. benzaldehyde
A)
3 and 4 only
done
clear
B)
3 and 5 only
done
clear
C)
1, 2 and 3 only
done
clear
D)
2, 3 and 5 only
done
clear
E)
5 only
done
clear
View Answer play_arrow
question_answer 82) Which compound among the following give/s positive iodoform test? 1. Ethanol 2. Ethanal 3. 1-butanol 4. 2-butanol 5. Phenyl ethanal
A)
1, 2 and 5
done
clear
B)
1, 3 and 4
done
clear
C)
1, 2 and 3
done
clear
D)
2, 4 and 5
done
clear
E)
1, 2 and 4
done
clear
View Answer play_arrow
question_answer 83) Amine that cannot be prepared by Gabriel phthalimide synthesis is
A)
aniline
done
clear
B)
benzylamine
done
clear
C)
methylamine
done
clear
D)
iso-butylamine
done
clear
E)
tertiary butylamine
done
clear
View Answer play_arrow
question_answer 84) Which of the following is the least basic amine?
A)
Ethylamine
done
clear
B)
Diethylamine
done
clear
C)
Aniline
done
clear
D)
Benzylamine
done
clear
E)
Methylamine
done
clear
View Answer play_arrow
question_answer 85) Which of the following bases is not present in DNA?
A)
Uracil
done
clear
B)
Adenine
done
clear
C)
Thymine
done
clear
D)
Guanine
done
clear
E)
Cytosine
done
clear
View Answer play_arrow
question_answer 86) Lactose is made of
A)
\[\alpha -\]D-glucose only
done
clear
B)
\[\alpha -\]D-glucose and\[\beta -\]D-glucose
done
clear
C)
\[\alpha -\]D-galactose and\[\beta -\]D-glucose
done
clear
D)
\[\beta -\]D-galactose and\[\beta -\]D-glucose
done
clear
E)
\[\beta -\]D-galactose and\[\beta -\]D-glucose
done
clear
View Answer play_arrow
question_answer 87) The artificial sweetener containing chlorine that has the appearance and taste as that of sugar and stable at cooking temperature is
A)
aspartame
done
clear
B)
saccharin
done
clear
C)
sucrolose
done
clear
D)
alitame
done
clear
E)
bithionol
done
clear
View Answer play_arrow
question_answer 88) Cetyltrimethyl ammonium bromide is a popular
A)
anionic detergent
done
clear
B)
cationic detergent
done
clear
C)
non-ionic detergent
done
clear
D)
sweetener
done
clear
E)
antioxidant
done
clear
View Answer play_arrow
question_answer 89) The number of electrons, neutrons and protons in a species are equal to 10, 8 and 8 respectively. The proper symbol of the species is
A)
\[_{8}^{16}O\]
done
clear
B)
\[_{8}^{18}O\]
done
clear
C)
\[_{10}^{18}Ne\]
done
clear
D)
\[_{8}^{16}{{O}^{-}}\]
done
clear
E)
\[_{8}^{16}{{O}^{2-}}\]
done
clear
View Answer play_arrow
question_answer 90) A 600 W mercury lamp emits monochromatic radiation of wavelength 331.3 nm. How many photons are emitted from the lamp per second? (\[h=6.626\times {{10}^{-34}}Js;\]velocity of light\[=3\times {{10}^{8}}m{{s}^{-1}}\])
A)
\[1\times {{10}^{19}}\]
done
clear
B)
\[1\times {{10}^{20}}\]
done
clear
C)
\[1\times {{10}^{21}}\]
done
clear
D)
\[1\times {{10}^{23}}\]
done
clear
E)
\[1\times {{10}^{22}}\]
done
clear
View Answer play_arrow
question_answer 91) The shortest wavelength in hydrogen spectrum of Lyman series when\[{{R}_{H}}=109678\] \[c{{m}^{-1}},\]is
A)
\[1002.7\,\overset{\text{o}}{\mathop{\text{A}}}\,\]
done
clear
B)
\[1215.67\,\overset{\text{o}}{\mathop{\text{A}}}\,\]
done
clear
C)
\[1127.30\,\overset{\text{o}}{\mathop{\text{A}}}\,\]
done
clear
D)
\[911.7\,\overset{\text{o}}{\mathop{\text{A}}}\,\]
done
clear
E)
\[1234.7\,\overset{\text{o}}{\mathop{\text{A}}}\,\]
done
clear
View Answer play_arrow
question_answer 92) Which of the following statements is false?
A)
\[{{H}_{2}}\]molecule has\[1\sigma \]bond
done
clear
B)
\[HCl\]molecule has\[1\sigma \]bond
done
clear
C)
Water molecule has\[2\sigma \]bonds and two lone pairs
done
clear
D)
Ethylene molecule has\[5\sigma \]bonds and In bond
done
clear
E)
Acetylene molecule has\[3\pi \]bonds and\[3\sigma \] bonds
done
clear
View Answer play_arrow
question_answer 93) \[{{N}_{2}}\]and\[{{O}_{2}}\]are converted to monopositive cations\[N_{2}^{+}\]and\[O_{2}^{+}\]respectively. Which is incorrect?
A)
In\[N_{2}^{+},\]the\[NN\]bond is weakened
done
clear
B)
In\[O_{2}^{+},\]the bond order increases
done
clear
C)
In\[O_{2}^{+},\] paramagnetism decreases
done
clear
D)
\[N_{2}^{+}\]becomes diamagnetic
done
clear
E)
Both\[{{O}_{2}},O_{2}^{+}\]are paramagnetic
done
clear
View Answer play_arrow
question_answer 94) A netural molecule\[X{{F}_{3}}\]has a zero dipole moment. The element X is most likely
A)
chlorine
done
clear
B)
boron
done
clear
C)
nitrogen
done
clear
D)
carbon
done
clear
E)
bromine
done
clear
View Answer play_arrow
question_answer 95) 56 g of nitrogen and 96 g of oxygen are mixed isothermalty and at a total pressure of 10 atm. The partial pressures of oxygen and nitrogen (in atm) are respectively
A)
4, 6
done
clear
B)
5, 5
done
clear
C)
2, 8
done
clear
D)
8, 2
done
clear
E)
6, 4
done
clear
View Answer play_arrow
question_answer 96) How much time (in hours) would it take to distribute one Avogadro number of wheat grains, if\[{{10}^{20}}\]grains are distributed each second?
A)
0.1673
done
clear
B)
1.673
done
clear
C)
16.73
done
clear
D)
167.3
done
clear
E)
1673
done
clear
View Answer play_arrow
question_answer 97)
The first\[({{\Delta }_{i}}{{H}_{1}})\]and second\[({{\Delta }_{i}}{{H}_{2}})\]ionisation enthalpies (in\[kJ\text{ }mo{{l}^{-1}}\]) and the\[({{\Delta }_{eg}}H)\]electron gain enthalpy (in\[kJ\text{ }mo{{l}^{-1}}\]) of the elements I, II, III, IV and V are given below Element \[{{\Delta }_{i}}{{H}_{1}}\] \[{{\Delta }_{i}}{{H}_{2}}\] \[{{\Delta }_{eg}}H\] I 520 7300 \[-\,60\] II 419 3051 \[-\,48\] III 1681 3374 \[-\,328\] IV 1008 1846 \[-\,295\] V 2372 5251 \[+\,48\]
The most reactive metal and the least reactive non-metal of these are respectively
A)
l and V
done
clear
B)
V and II
done
clear
C)
II and V
done
clear
D)
IV and V
done
clear
E)
V and III
done
clear
View Answer play_arrow
question_answer 98) Which of the following undergoes reduction with hydrogen peroxide in alkaline medium?
A)
\[M{{n}^{2+}}\]
done
clear
B)
\[HOCl\]
done
clear
C)
\[PbS\]
done
clear
D)
\[F{{e}^{2+}}\]
done
clear
E)
\[{{I}_{2}}\]
done
clear
View Answer play_arrow
question_answer 99) According to Ellingham diagram, the oxidation reaction of carbon to carbon monoxide may be used to reduce which one of the following oxides at the lowest temperature?
A)
\[A{{l}_{2}}{{O}_{3}}\]
done
clear
B)
\[C{{u}_{2}}O\]
done
clear
C)
\[MgO\]
done
clear
D)
\[ZnO\]
done
clear
E)
\[FeO\]
done
clear
View Answer play_arrow
question_answer 100) The metal that produces red-violet colour in the non-luminous flame is
A)
Ba
done
clear
B)
Ag
done
clear
C)
Rb
done
clear
D)
Pb
done
clear
E)
Zn
done
clear
View Answer play_arrow
question_answer 101) Halogens exist in\[-1,+\text{ }1,+3,+5\]and +7 oxidation states. The halogen that exists only in\[-1\]state is
A)
\[F\]
done
clear
B)
\[Cl\]
done
clear
C)
\[Br\]
done
clear
D)
\[I\]
done
clear
E)
\[At\]
done
clear
View Answer play_arrow
question_answer 102) Among the oxyacids of phosphorus, the dibasic acid is
A)
\[{{H}_{4}}{{P}_{2}}{{O}_{7}}\]
done
clear
B)
\[{{H}_{3}}P{{O}_{2}}\]
done
clear
C)
\[HP{{O}_{3}}\]
done
clear
D)
\[{{H}_{3}}P{{O}_{4}}\]
done
clear
E)
\[{{H}_{3}}P{{O}_{3}}\]
done
clear
View Answer play_arrow
question_answer 103)
Pick out the correct statement(s). 1. Manganese exhibits + 7 oxidation state 2. Zinc forms coloured ions 3.\[{{[Co{{F}_{6}}]}^{3-}}\]is diamagnetic 4. Sc forms +4 oxidation state 5. Zn exhibits only +2 oxidation state
A)
1 and 2
done
clear
B)
1 and 5
done
clear
C)
2 and 4
done
clear
D)
3 and 4
done
clear
E)
2 and 5
done
clear
View Answer play_arrow
question_answer 104) The maximum oxidation state exhibited by actinide ions is
A)
+5
done
clear
B)
+4
done
clear
C)
+7
done
clear
D)
+8
done
clear
E)
+6
done
clear
View Answer play_arrow
question_answer 105) Calculate the standard enthalpy change (in kJ \[mo{{l}^{-1}}\]) for the reaction \[{{H}_{2}}(g)+{{O}_{2}}(g)\xrightarrow{{}}{{H}_{2}}{{O}_{2}}(g)\] Given that bond enthalpies of\[HH,\text{ O}=O,\]\[OH\]and\[OO\](in kJ\[mo{{l}^{-1}}\]) are respectively 438, 498, 464 and 138.
A)
\[-130\]
done
clear
B)
\[-\,65\]
done
clear
C)
+ 130
done
clear
D)
\[-\,334\]
done
clear
E)
+ 334
done
clear
View Answer play_arrow
question_answer 106) According to the first law of thermodynamics which of the following quantities represents the change in a state function?
A)
\[{{q}_{rev}}\]
done
clear
B)
\[{{q}_{rev}}-{{W}_{rev}}\]
done
clear
C)
\[{{q}_{rev}}/{{W}_{rev}}\]
done
clear
D)
\[{{W}_{rev}}\]
done
clear
E)
\[{{q}_{rev}}+{{W}_{rev}}\]
done
clear
View Answer play_arrow
question_answer 107) The aqueous solution of which of the salt has pH close to 7?
A)
\[FeC{{l}_{3}}\]
done
clear
B)
\[C{{H}_{3}}COONa\]
done
clear
C)
\[N{{a}_{2}}C{{O}_{3}}\]
done
clear
D)
\[C{{H}_{3}}COON{{H}_{4}}\]
done
clear
E)
\[KCN\]
done
clear
View Answer play_arrow
question_answer 108) Consider the following reactions in which all the reactants and the products are in gaseous state. \[2PQ{{P}_{2}}+{{Q}_{2}};\] \[{{K}_{1}}=2.5\times {{10}^{5}}\] \[PQ+\frac{1}{2}{{R}_{2}}PQR;\] \[{{K}_{2}}=5\times {{10}^{-3}}\] The value of\[{{K}_{3}}\]for the equilibrium \[\frac{1}{2}{{P}_{2}}+\frac{1}{2}{{Q}_{2}}+\frac{1}{2}{{R}_{2}}PQR,\]is
A)
\[2.5\times {{10}^{-3}}\]
done
clear
B)
\[2.5\times {{10}^{3}}\]
done
clear
C)
\[1.0\times {{10}^{-5}}\]
done
clear
D)
\[5\times {{10}^{3}}\]
done
clear
E)
\[5\times {{10}^{-3}}\]
done
clear
View Answer play_arrow
question_answer 109) The amount of solute (molar mass\[60\text{ }g\text{ }mo{{l}^{-1}}\]) that must be added to 180 g of water so that the vapour pressure of water is lowered by 10%, is
A)
30 g
done
clear
B)
60 g
done
clear
C)
120 g
done
clear
D)
12 g
done
clear
E)
24 g
done
clear
View Answer play_arrow
question_answer 110) 200 mL of water is added to a 500 mL of 0.2 M solution. What is the molarity of this diluted solution?
A)
0.5010 M
done
clear
B)
0.2897 M
done
clear
C)
0.7093 M
done
clear
D)
0.1428 M
done
clear
E)
0.4005 M
done
clear
View Answer play_arrow
question_answer 111) Which of the following species can function both as oxidising as well as reducing agent?
A)
\[C{{l}^{-}}\]
done
clear
B)
\[ClO_{4}^{-}\]
done
clear
C)
\[Cl{{O}^{-}}\]
done
clear
D)
\[MnO_{4}^{-}\]
done
clear
E)
\[NO_{3}^{-}\]
done
clear
View Answer play_arrow
question_answer 112) One Faraday of electricity is passed through molten\[A{{l}_{2}}{{O}_{3}},\]aqueous solution of\[CuS{{O}_{4}}\]and molten\[NaCl\]taken in three different electrolytic cells connected in series. The mole ratio of\[Al,Cu\]and Na deposited at the respective cathode is
A)
2 : 3 : 6
done
clear
B)
\[6:2:3\]
done
clear
C)
6 : 3 : 2
done
clear
D)
\[1:2:3\]
done
clear
E)
3 : 6 : 2
done
clear
View Answer play_arrow
question_answer 113) Half-lives of a first order and a zero order reactions are same. Then, the ratio of the initial rates of first order reaction to that of the zero order reaction is
A)
\[\frac{1}{0.93}\]
done
clear
B)
\[2\times 0.693\]
done
clear
C)
0.693
done
clear
D)
\[\frac{2}{0.693}\]
done
clear
E)
6.93
done
clear
View Answer play_arrow
question_answer 114) If the activation energy for the forward reaction is\[150\text{ }kJ\text{ }mo{{l}^{-1}}\]and that of the reverse reaction is\[260\text{ }kJ\text{ }mo{{l}^{-1}},\] what is the enthalpy change for the reaction?
A)
\[410\text{ }kJ\text{ }mo{{l}^{-1}}\]
done
clear
B)
\[110\,kJ\,mo{{l}^{-1}}\]
done
clear
C)
\[-110\,kJ\,mo{{l}^{-1}}\]
done
clear
D)
\[-\,410\,kJ\,mo{{l}^{-1}}\]
done
clear
E)
\[90\,kJ\,mo{{l}^{-1}}\]
done
clear
View Answer play_arrow
question_answer 115) The dispersed phase and dispersion medium in soap lather are respectively
A)
gas and liquid
done
clear
B)
liquid and gas
done
clear
C)
solid and gas
done
clear
D)
solid and liquid
done
clear
E)
gas and solid
done
clear
View Answer play_arrow
question_answer 116) In petrochemical industry, alcohols are directly converted to gasoline by passing over heated
A)
platinum
done
clear
B)
ZSM-5
done
clear
C)
iron
done
clear
D)
nickel
done
clear
E)
palladium
done
clear
View Answer play_arrow
question_answer 117)
Which among the following statements are true for the complex\[[Co{{(N{{H}_{3}})}_{6}}][Cr{{(CN)}_{6}}]\]? 1. It is a non-electrolyte 2. The magnitude of the charge on each complex ion is 3 3. The complex will not conduct current 4. The complex will exhibit coordination isomerism 5. The magnitude of the charge on each complex ion is 1
A)
1 and 4
done
clear
B)
1 and 2
done
clear
C)
1 and 3
done
clear
D)
3 and 5
done
clear
E)
2 and 4
done
clear
View Answer play_arrow
question_answer 118) An example of ambidentate ligand is
A)
ammine
done
clear
B)
aquo
done
clear
C)
chloro
done
clear
D)
oxalato
done
clear
E)
thiocyanato
done
clear
View Answer play_arrow
question_answer 119) In Lassaignes test for the detection of halogens, the sodium fusion extract is first boiled with concentrated nitric acid. This is
A)
to remove silver halides
done
clear
B)
to decompose\[N{{a}_{2}}S\]and\[NaCN,\]if present
done
clear
C)
to dissolve \[A{{g}_{2}}S\]
done
clear
D)
to dissolve\[AgCN,\]if formed
done
clear
E)
because\[A{{g}_{2}}S\]and\[AgCN\]are insoluble in nitric acid
done
clear
View Answer play_arrow
question_answer 120) All carbon atoms are\[s{{p}^{2}}-\]hybridised in
A)
1, 3-butadiene
done
clear
B)
\[C{{H}_{2}}=C=C{{H}_{2}}\]
done
clear
C)
cyclohexane
done
clear
D)
2-butene
done
clear
E)
\[CH\equiv CC\equiv CH\]
done
clear
View Answer play_arrow
question_answer 121) One of the points on the parabola\[{{y}^{2}}=12x\]with focal distance 12, is
A)
(3, 6)
done
clear
B)
\[(9,6\sqrt{3})\]
done
clear
C)
\[(7,2\sqrt{21})\]
done
clear
D)
\[(8,4\sqrt{6})\]
done
clear
E)
\[(1,\sqrt{12})\]
done
clear
View Answer play_arrow
question_answer 122) If the length of the major axis of an ellipse is\[\frac{17}{8}\]times the length of the minor axis, then the eccentricity of the ellipse is
A)
\[\frac{8}{17}\]
done
clear
B)
\[\frac{15}{17}\]
done
clear
C)
\[\frac{9}{17}\]
done
clear
D)
\[\frac{2\sqrt{2}}{17}\]
done
clear
E)
\[\frac{13}{17}\]
done
clear
View Answer play_arrow
question_answer 123) If a point\[P(x,\text{ }y)\]moves along the ellipse \[\frac{{{x}^{2}}}{25}+\frac{{{y}^{2}}}{16}=1\]and if C is the centre of the ellipse, then the sum of maximum and minimum values of CP is
A)
25
done
clear
B)
9
done
clear
C)
4
done
clear
D)
5
done
clear
E)
16
done
clear
View Answer play_arrow
question_answer 124) The distance between the foci of the conic \[7{{x}^{2}}-9{{y}^{2}}=63\]is equal to
A)
8
done
clear
B)
4
done
clear
C)
3
done
clear
D)
7
done
clear
E)
12
done
clear
View Answer play_arrow
question_answer 125) If\[|\overrightarrow{a}|=5,|\overrightarrow{b}|=6\]and\[\overrightarrow{a}.\overrightarrow{b}=-25,\]then\[|\overrightarrow{a}\times \overrightarrow{b}|\]is equal to
A)
25
done
clear
B)
\[6\sqrt{11}\]
done
clear
C)
\[11\sqrt{5}\]
done
clear
D)
\[11\sqrt{6}\]
done
clear
E)
\[5\sqrt{11}\]
done
clear
View Answer play_arrow
question_answer 126) If\[\overrightarrow{p},\overrightarrow{q}\]and\[\overrightarrow{r}\]are perpendicular to\[\overrightarrow{q}+\overrightarrow{r},\overrightarrow{r}+\overrightarrow{p}\]and\[\overrightarrow{p}+\overrightarrow{q}\]respectively and if\[|\overrightarrow{p}+\overrightarrow{q}|=6,\]\[|\overrightarrow{q}+\overrightarrow{r}|=4\sqrt{3}\]and\[|\overrightarrow{r}+\overrightarrow{p}|=4,\]then\[|\overrightarrow{p}+\overrightarrow{q}+\overrightarrow{r}|\]is
A)
\[5\sqrt{2}\]
done
clear
B)
10
done
clear
C)
15
done
clear
D)
5
done
clear
E)
25
done
clear
View Answer play_arrow
question_answer 127) The vectors of magnitude a, 2a, 3a meet at a point and their directions are along the diagonals of three adjacent faces of a cube. Then, the magnitude of their resultant is
A)
\[5a\]
done
clear
B)
\[6a\]
done
clear
C)
\[10a\]
done
clear
D)
\[9a\]
done
clear
E)
\[7a\]
done
clear
View Answer play_arrow
question_answer 128) Which one of the following vectors is of magnitude 6 and perpendicular to both \[\overrightarrow{a}=2\hat{i}+2\hat{j}+\hat{k}\]and\[\overrightarrow{b}=\hat{i}-2\hat{j}+2\hat{k}?\]
A)
\[2\hat{i}+\hat{j}-2\hat{k}\]
done
clear
B)
\[2(2\hat{i}-\hat{j}+2\hat{k})\]
done
clear
C)
\[3(2\hat{i}-\hat{j}-2\hat{k})\]
done
clear
D)
\[2(2\hat{i}+\hat{j}-2\hat{k})\]
done
clear
E)
\[2(2\hat{i}-\hat{j}-2\hat{k})\]
done
clear
View Answer play_arrow
question_answer 129) If the vectors\[\overrightarrow{a}=2\hat{i}+\hat{j}+4\hat{k},\overrightarrow{b}=4\hat{i}-2\hat{j}+3\hat{k}\]and\[\overrightarrow{c}=2\hat{i}-3\hat{j}-\lambda \hat{k}\]are coplanar, then the value of k is equal to
A)
2
done
clear
B)
1
done
clear
C)
3
done
clear
D)
\[-1\]
done
clear
E)
0
done
clear
View Answer play_arrow
question_answer 130) Let\[A(1,-1,2)\]and\[B(2,3,-1)\]be two points. If a point P divides AB internally in the ratio\[2:3,\]then the position vector of P is
A)
\[\frac{1}{\sqrt{5}}(\hat{i}+\hat{j}+\hat{k})\]
done
clear
B)
\[\frac{1}{\sqrt{3}}(\hat{i}+6\hat{j}+\hat{k})\]
done
clear
C)
\[\frac{1}{\sqrt{3}}(\hat{i}+\hat{j}+\hat{k})\]
done
clear
D)
\[\frac{1}{5}(7\hat{i}+3\hat{j}+4\hat{k})\]
done
clear
E)
\[\frac{1}{\sqrt{5}}(\hat{i}+\hat{j}+9\hat{k})\]
done
clear
View Answer play_arrow
question_answer 131) If the scalar product of the vector \[\hat{i}+\hat{j}+2\hat{k}\]with the unit vector along\[m\hat{i}+2\hat{j}+3\hat{k}\]is equal to 2, then one of the values of m is
A)
3
done
clear
B)
4
done
clear
C)
5
done
clear
D)
6
done
clear
E)
7
done
clear
View Answer play_arrow
question_answer 132) A plane makes intercepts a, b, c at A, B, C on the coordinate axes respectively. If the centroid of the\[\Delta ABC\]is at (3, 2, 1), then the equation of the plane is
A)
\[x+2y+3z=9\]
done
clear
B)
\[2x-3y-6z=18\]
done
clear
C)
\[2x+3y+6z=18\]
done
clear
D)
\[2x+y+6z=18\]
done
clear
E)
\[2x+3y+6z=9\]
done
clear
View Answer play_arrow
question_answer 133) If the plane\[3x+y+2z+6=0\]is parallel to the line\[\frac{3x-1}{2b}=3-y=\frac{z-1}{a},\]then the value of \[3a+3b\]is
A)
\[\frac{1}{2}\]
done
clear
B)
\[\frac{3}{2}\]
done
clear
C)
\[3\]
done
clear
D)
\[4\]
done
clear
E)
\[\frac{5}{2}\]
done
clear
View Answer play_arrow
question_answer 134) The equation of the line passing through the point\[(3,0,-4)\]and perpendicular to the plane \[2x-3y+5z-7=0\]is
A)
\[\frac{x-2}{3}=\frac{y}{-3}=\frac{z+4}{5}\]
done
clear
B)
\[\frac{x-3}{2}=\frac{y}{-3}=\frac{z-4}{5}\]
done
clear
C)
\[\frac{x-3}{2}=\frac{-y}{3}=\frac{z+4}{5}\]
done
clear
D)
\[\frac{x+3}{2}=\frac{y}{3}=\frac{z-4}{5}\]
done
clear
E)
\[\frac{x-2}{3}=\frac{y}{3}=\frac{z+4}{5}\]
done
clear
View Answer play_arrow
question_answer 135) The plane \[\overrightarrow{r}=s(\hat{i}+2\hat{j}-4\hat{k})+t(3\hat{i}+4\hat{j}-4\hat{k})\] \[+(1-t)(2\hat{i}-7\hat{j}-3\hat{k})\] is parallel to the line
A)
\[\overrightarrow{r}=(-\hat{i}+\hat{j}-\hat{k})+t(-\hat{i}-2\hat{j}+4\hat{k})\]
done
clear
B)
\[\overrightarrow{r}=(-\hat{i}+\hat{j}-\hat{k})+t(\hat{i}-2\hat{j}+4\hat{k})\]
done
clear
C)
\[\overrightarrow{r}=(\hat{i}+\hat{j}-\hat{k})+t(-\hat{i}-4\hat{j}+7\hat{k})\]
done
clear
D)
\[\overrightarrow{r}=(-\hat{i}+\hat{j}-\hat{k})+t(-2\hat{i}+2\hat{j}+4\hat{k})\]
done
clear
E)
\[\overrightarrow{r}=(-\hat{i}+\hat{j}-3\hat{k})+t(2\hat{i}+6\hat{j}-8\hat{k})\]
done
clear
View Answer play_arrow
question_answer 136) The distance between the line\[\overrightarrow{r}=(2\hat{i}+2\hat{j}-\hat{k})+\lambda (2\hat{i}+\hat{j}-2\hat{k})\]and the plane\[\overrightarrow{r}.(\hat{i}+2\hat{j}+2\hat{k})=10\]is equal to
A)
5
done
clear
B)
4
done
clear
C)
3
done
clear
D)
2
done
clear
E)
1
done
clear
View Answer play_arrow
question_answer 137) Equation of the plane passing through the intersection of the planes\[x+y+z=6\]and \[2x+3y+4z+5=0\]and the point (1, 1, 1) is
A)
\[20x+23y+26z-69=0\]
done
clear
B)
\[31x+45y+49z+52=0\]
done
clear
C)
\[8x+5y+2z-69=0\]
done
clear
D)
\[4x+5y+6z-7=0\]
done
clear
E)
\[x+y+2z+17=0\]
done
clear
View Answer play_arrow
question_answer 138) The equation of the plane containing the lines \[\frac{x-1}{2}=\frac{y+1}{-1}=\frac{z}{3}\]and\[\frac{x}{2}=\frac{y-2}{-1}=\frac{z+1}{3}\]is
A)
\[8x-y+5z-8=0\]
done
clear
B)
\[8x+y-5z-7=0\]
done
clear
C)
\[x-8y+3z+6=0\]
done
clear
D)
\[8x+y-5z+7=0\]
done
clear
E)
\[x+y+z-6=0\]
done
clear
View Answer play_arrow
question_answer 139) The vector equation of the straight line \[\frac{1-x}{3}=\frac{y+1}{-2}\,=\frac{3-z}{-1}\]
A)
\[\overrightarrow{r}=(\hat{i}-\hat{j}+3\hat{k})+\lambda (3\hat{i}+2\hat{j}-\hat{k})\]
done
clear
B)
\[\overrightarrow{r}=(\hat{i}-\hat{j}+3\hat{k})+\lambda (3\hat{i}-2\hat{j}-\hat{k})\]
done
clear
C)
\[\overrightarrow{r}=(3\hat{i}-2\hat{j}-\hat{k})+\lambda (\hat{i}-\hat{j}+3\hat{k})\]
done
clear
D)
\[\overrightarrow{r}=(3\hat{i}+2\hat{j}-\hat{k})+\lambda (\hat{i}-\hat{j}+3\hat{k})\]
done
clear
E)
\[\overrightarrow{r}=(\hat{i}-\hat{j}+3\hat{k})+\lambda (3\hat{i}+2\hat{j}+\hat{k})\]
done
clear
View Answer play_arrow
question_answer 140) The arithmetic mean of 7 consecutive integers starting with a is m. Then, the arithmetic mean of 11 consecutive integers starting with \[a+2\]is
A)
\[2a\]
done
clear
B)
\[2m\]
done
clear
C)
\[a+4\]
done
clear
D)
\[m+4\]
done
clear
E)
\[a+m+2\]
done
clear
View Answer play_arrow
question_answer 141)
The probability distribution of a random variable\[X\]is given as \[x\] -5 -4 -3 -2 -1 0 1 2 3 4 5 \[P(X=x)\] P 2p 3p 4p 5p 7p 8p 9p 10p 11p 12p
Then, the value of p is
A)
\[\frac{1}{72}\]
done
clear
B)
\[\frac{3}{73}\]
done
clear
C)
\[\frac{5}{72}\]
done
clear
D)
\[\frac{1}{74}\]
done
clear
E)
\[\frac{1}{73}\]
done
clear
View Answer play_arrow
question_answer 142) The mean and variance of n observations\[{{x}_{1}},{{x}_{2}},{{x}_{3}},......,{{x}_{n}}\]and 0 respectively. If\[\sum\limits_{i=1}^{n}{x_{i}^{2}}=400,\]then the value of n is equal to
A)
80
done
clear
B)
25
done
clear
C)
20
done
clear
D)
16
done
clear
E)
4
done
clear
View Answer play_arrow
question_answer 143) If A and B are mutually exclusive events and if\[p(B)=\frac{1}{3},p(A\cup B)=\frac{13}{21},\]then P is equal to
A)
\[\frac{1}{7}\]
done
clear
B)
\[\frac{4}{7}\]
done
clear
C)
\[\frac{2}{7}\]
done
clear
D)
\[\frac{5}{7}\]
done
clear
E)
\[\frac{6}{7}\]
done
clear
View Answer play_arrow
question_answer 144) If\[f\]is a real valued function such that\[f(x+y)=f(x)+f(y)\]and\[f(1)=5,\]then the value of f(100) is
A)
200
done
clear
B)
300
done
clear
C)
350
done
clear
D)
400
done
clear
E)
500
done
clear
View Answer play_arrow
question_answer 145) Let\[f(x)=\frac{{{({{e}^{x}}-1)}^{2}}}{\sin \left( \frac{x}{a} \right)\log \left( 1+\frac{x}{4} \right)}\]for\[x\ne 0\]and \[f(0)=12,\]If\[f\]is continuous at\[x=0,\]then the value of a is equal to
A)
1
done
clear
B)
\[-1\]
done
clear
C)
2
done
clear
D)
\[-2\]
done
clear
E)
3
done
clear
View Answer play_arrow
question_answer 146) \[\underset{x\to 0}{\mathop{\lim }}\,\left( \frac{x}{\sqrt{1+x}-\sqrt{1-x}} \right)\]is equal to
A)
0
done
clear
B)
1
done
clear
C)
2
done
clear
D)
\[-1\]
done
clear
E)
\[-2\]
done
clear
View Answer play_arrow
question_answer 147) \[\underset{x\to \infty }{\mathop{\lim }}\,\left( \frac{{{x}^{3}}}{3{{x}^{2}}-4}-\frac{{{x}^{2}}}{3x+2} \right)\]is equal to
A)
\[-\frac{1}{4}\]
done
clear
B)
\[-\frac{1}{2}\]
done
clear
C)
\[0\]
done
clear
D)
\[\frac{2}{9}\]
done
clear
E)
\[-\frac{6}{5}\]
done
clear
View Answer play_arrow
question_answer 148) If\[{{x}^{y}}={{e}^{2(x-y)}},\]then\[\frac{dy}{dx}\]is equal to
A)
\[\frac{2(1+\log x)}{{{(2+\log x)}^{2}}}\]
done
clear
B)
\[\frac{1+\log x}{{{(2+\log x)}^{2}}}\]
done
clear
C)
\[\frac{2}{2+\log x}\]
done
clear
D)
\[\frac{2(1-\log x)}{{{(2+\log x)}^{2}}}\]
done
clear
E)
\[\frac{2+\log x}{{{(2+\log x)}^{2}}}\]
done
clear
View Answer play_arrow
question_answer 149) If\[y={{\sin }^{-1}}\sqrt{1-x},\]then\[\frac{dy}{dx}\]is equal to
A)
\[\frac{1}{\sqrt{1-x}}\]
done
clear
B)
\[\frac{-1}{2\sqrt{1-x}}\]
done
clear
C)
\[\frac{1}{\sqrt{x}}\]
done
clear
D)
\[\frac{-1}{2\sqrt{x}\sqrt{1-x}}\]
done
clear
E)
\[\frac{1}{\sqrt{x}\sqrt{1-x}}\]
done
clear
View Answer play_arrow
question_answer 150) The derivative of\[{{\sin }^{-1}}(2x\sqrt{1-{{x}^{2}}})\]with respect to\[{{\sin }^{-1}}(3x-4{{x}^{3}})\]is
A)
\[\frac{2}{3}\]
done
clear
B)
\[\frac{3}{2}\]
done
clear
C)
\[\frac{1}{2}\]
done
clear
D)
\[1\]
done
clear
E)
\[0\]
done
clear
View Answer play_arrow
question_answer 151) If\[y={{\tan }^{-1}}x+{{\sec }^{-1}}x+{{\cot }^{-1}}x+\cos e{{c}^{-1}}x,\]then \[\frac{dy}{dx}\]is equal to
A)
\[\frac{{{x}^{2}}-1}{{{x}^{2}}+1}\]
done
clear
B)
\[\pi \]
done
clear
C)
\[0\]
done
clear
D)
\[1\]
done
clear
E)
\[\frac{1}{x\sqrt{{{x}^{2}}-1}}\]
done
clear
View Answer play_arrow
question_answer 152) If\[f(x)=|x-2|+|x+1|-x,\]then\[f(-10)\]is equal to
A)
\[-3\]
done
clear
B)
\[-2\]
done
clear
C)
\[-1\]
done
clear
D)
\[0\]
done
clear
E)
\[1\]
done
clear
View Answer play_arrow
question_answer 153) If\[x=a(1+\cos \theta ),y=a(\theta +\sin \theta ),\]then \[\frac{{{d}^{2}}y}{d{{x}^{2}}}\]at \[\theta =\frac{\pi }{2}\]is
A)
\[-\frac{1}{a}\]
done
clear
B)
\[\frac{1}{a}\]
done
clear
C)
\[-1\]
done
clear
D)
\[-2\]
done
clear
E)
\[-\frac{2}{a}\]
done
clear
View Answer play_arrow
question_answer 154) If\[y={{\tan }^{-1}}\left( \frac{\cos x}{1+\sin x} \right),\]then\[\frac{dy}{dx}\]is equal to
A)
\[\frac{1}{2}\]
done
clear
B)
\[2\]
done
clear
C)
\[-2\]
done
clear
D)
\[-\frac{1}{2}\]
done
clear
E)
\[-1\]
done
clear
View Answer play_arrow
question_answer 155) The distance between the origin and the normal to the curve\[y={{e}^{2x}}+{{x}^{2}}\]at\[x=0\]is
A)
\[2\]
done
clear
B)
\[\frac{2}{\sqrt{3}}\]
done
clear
C)
\[\frac{2}{\sqrt{5}}\]
done
clear
D)
\[\frac{1}{2}\]
done
clear
E)
\[\frac{1}{\sqrt{5}}\]
done
clear
View Answer play_arrow
question_answer 156) The value of c in (0, 2) satisfying the mean value theorem for the function\[f(x)=x{{(x-1)}^{2}},x\in [0,2]\]is equal to
A)
\[\frac{3}{4}\]
done
clear
B)
\[\frac{4}{3}\]
done
clear
C)
\[\frac{1}{3}\]
done
clear
D)
\[\frac{2}{3}\]
done
clear
E)
\[\frac{5}{3}\]
done
clear
View Answer play_arrow
question_answer 157) The point on the curve\[{{x}^{2}}+{{y}^{2}}={{a}^{2}},\text{ }y\ge 0\]at which the tangent is parallel to\[x-\]axis is
A)
\[(a,0)\]
done
clear
B)
\[(-a,0)\]
done
clear
C)
\[\left( \frac{a}{2},\frac{\sqrt{3}}{2}a \right)\]
done
clear
D)
\[(0,a)\]
done
clear
E)
\[(0,{{a}^{2}})\]
done
clear
View Answer play_arrow
question_answer 158) The angle between the curves,\[y={{x}^{2}}\]and \[{{y}^{2}}-x=0\]at the point (1, 1), is
A)
\[\frac{\pi }{2}\]
done
clear
B)
\[{{\tan }^{-1}}\frac{4}{3}\]
done
clear
C)
\[\frac{\pi }{3}\]
done
clear
D)
\[\frac{\pi }{4}\]
done
clear
E)
\[{{\tan }^{-1}}\frac{3}{4}\]
done
clear
View Answer play_arrow
question_answer 159) An edge of a variable cube is increasing at the rate of 10 cm/s. How fast the volume of the cube will increase when the edge is 5 cm long?
A)
\[750\text{ }c{{m}^{3}}/s\]
done
clear
B)
\[75\,c{{m}^{3}}/s\]
done
clear
C)
\[300\text{ }c{{m}^{3}}/s\]
done
clear
D)
\[150\,\,c{{m}^{3}}/s\]
done
clear
E)
\[25c{{m}^{3}}/s\]
done
clear
View Answer play_arrow
question_answer 160) The minimum value of\[f(x)=|3-x|+7\]is
A)
0
done
clear
B)
6
done
clear
C)
7
done
clear
D)
8
done
clear
E)
10
done
clear
View Answer play_arrow
question_answer 161) If the error committed in measuring the radius of the circle is 0.05%, then the corresponding error in calculating the area is
A)
0.05%
done
clear
B)
0.0025%
done
clear
C)
0.25%
done
clear
D)
0.1%
done
clear
E)
0.2%
done
clear
View Answer play_arrow
question_answer 162) If\[\int{\frac{x+2}{2{{x}^{2}}+6x+5}}dx\] \[=P\int{\frac{4x+6}{2{{x}^{2}}+6x+5}}dx+\frac{1}{2}\int{\frac{dx}{2{{x}^{2}}+6x+5}},\] then the values of\[P\]is
A)
\[\frac{1}{3}\]
done
clear
B)
\[\frac{1}{2}\]
done
clear
C)
\[\frac{1}{4}\]
done
clear
D)
\[2\]
done
clear
E)
\[1\]
done
clear
View Answer play_arrow
question_answer 163) \[\int{(x+1){{(x+2)}^{7}}}(x+3)dx\]is equal to
A)
\[\frac{{{(x+2)}^{10}}}{10}-\frac{{{(x+2)}^{8}}}{8}+C\]
done
clear
B)
\[\frac{{{(x+1)}^{2}}}{2}-\frac{{{(x+2)}^{8}}}{8}-\frac{{{(x+3)}^{2}}}{2}+C\]
done
clear
C)
\[\frac{{{(x+2)}^{10}}}{10}+C\]
done
clear
D)
\[\frac{{{(x+1)}^{2}}}{2}+\frac{{{(x+2)}^{8}}}{8}+\frac{{{(x+3)}^{2}}}{2}+C\]
done
clear
E)
\[\frac{{{(x+2)}^{9}}}{9}-\frac{{{(x+2)}^{7}}}{7}+C\]
done
clear
View Answer play_arrow
question_answer 164) \[\int{({{x}^{2}}+1)}\sqrt{x+1}dx\]is equal to
A)
\[\frac{{{(x+1)}^{7/2}}}{7}-2\frac{{{(x+1)}^{5/2}}}{5}\]\[+2\frac{{{(x+1)}^{3/2}}}{3}+C\]
done
clear
B)
\[2\left[ \frac{{{(x+1)}^{7/2}}}{7}-2\frac{{{(x+1)}^{5/2}}}{5} \right.\]\[\left. +2\frac{{{(x+1)}^{3/2}}}{3} \right]+c\]
done
clear
C)
\[\frac{{{(x+1)}^{7/2}}}{7}-2\frac{{{(x+1)}^{5/2}}}{5}+c\]
done
clear
D)
\[\frac{{{(x+1)}^{7/2}}}{7}-3\frac{{{(x+1)}^{5/2}}}{5}\]\[+11{{(x+1)}^{1/2}}+c\]
done
clear
E)
\[{{(x+1)}^{7/2}}+{{(x+1)}^{5/2}}+{{(x+1)}^{3/2}}+c\]
done
clear
View Answer play_arrow
question_answer 165) \[\int{\frac{1+x}{x+{{e}^{-x}}}}\]is equal to
A)
\[\log |(x-{{e}^{-x}})|+c\]
done
clear
B)
\[\log |(x+{{e}^{-x}})|+c\]
done
clear
C)
\[\log |(1+x{{e}^{x}})|+c\]
done
clear
D)
\[{{(1+x{{e}^{x}})}^{2}}+c\]
done
clear
E)
\[\log |(1-x{{e}^{x}})|+c\]
done
clear
View Answer play_arrow
question_answer 166) \[\int{\frac{\log (x+\sqrt{1+{{x}^{2}}})}{\sqrt{1+{{x}^{2}}}}}dx\]is equal to
A)
\[{{[\log (x+\sqrt{1+{{x}^{2}}})]}^{2}}+c\]
done
clear
B)
\[x\log (x+\sqrt{1+{{x}^{2}}})+c\]
done
clear
C)
\[\frac{1}{2}\log (x+\sqrt{1+{{x}^{2}}})+c\]
done
clear
D)
\[\frac{1}{2}{{[\log (x+\sqrt{1+{{x}^{2}}})]}^{2}}+c\]
done
clear
E)
\[\frac{x}{2}\log (x+\sqrt{1+{{x}^{2}}})+c\]
done
clear
View Answer play_arrow
question_answer 167) \[\int{\frac{dx}{\sqrt{1-{{e}^{2x}}}}}\]is equal to
A)
\[\log |{{e}^{-x}}+\sqrt{{{e}^{-2x}}-1}|+c\]
done
clear
B)
\[\log |{{e}^{x}}+\sqrt{{{e}^{2x}}-1}|+c\]
done
clear
C)
\[-\log |{{e}^{-x}}+\sqrt{{{e}^{-2x}}-1}|+c\]
done
clear
D)
\[-\log |{{e}^{-2x}}+\sqrt{{{e}^{-2x}}-1}|+c\]
done
clear
E)
\[\log |{{e}^{-2x}}+\sqrt{{{e}^{-2x}}-1}|+c\]
done
clear
View Answer play_arrow
question_answer 168) \[\int{\frac{\cos x+x\sin x}{{{x}^{2}}+x\cos x}}\]is equal to
A)
\[\log \left| \frac{\sin x}{1+\cos x} \right|+c\]
done
clear
B)
\[\log \left| \frac{\sin x}{x+\cos x} \right|+c\]
done
clear
C)
\[\log \left| \frac{2\sin x}{x+\cos x} \right|+c\]
done
clear
D)
\[\log \left| \frac{x\sin x}{x+\cos x} \right|+c\]
done
clear
E)
\[\log \left| \frac{x}{x+\cos x} \right|+c\]
done
clear
View Answer play_arrow
question_answer 169) The integral\[\int_{0}^{1}{\frac{2{{\sin }^{-1}}\frac{x}{2}}{x}}dx\] equals
A)
\[\int_{0}^{\pi /6}{\frac{xdx}{\tan x}}\]
done
clear
B)
\[\int_{0}^{\pi /6}{\frac{2x}{\tan x}}dx\]
done
clear
C)
\[\int_{0}^{\pi /2}{\frac{2xdx}{\tan x}}\]
done
clear
D)
\[\int_{0}^{\pi /6}{\frac{xdx}{\sin x}}\]
done
clear
E)
\[\int_{0}^{\pi /6}{\frac{2x}{\sin x}}dx\]
done
clear
View Answer play_arrow
question_answer 170) The area of the plane region bounded by the curve\[x={{y}^{2}}-2\]and the line\[y=-x\]is (in square units)
A)
\[\frac{13}{3}\]
done
clear
B)
\[\frac{2}{5}\]
done
clear
C)
\[\frac{9}{5}\]
done
clear
D)
\[\frac{5}{2}\]
done
clear
E)
\[\frac{13}{2}\]
done
clear
View Answer play_arrow
question_answer 171) If\[\int_{0}^{a}{f(2a-x)dx}=m\]and\[\int_{0}^{a}{f(x)dx}=n,\]then\[\int_{0}^{2a}{f(x)dx}\]is equal to
A)
\[2m+n\]
done
clear
B)
\[m+2n\]
done
clear
C)
\[m-n\]
done
clear
D)
\[n-m\]
done
clear
E)
\[m+n\]
done
clear
View Answer play_arrow
question_answer 172) \[\int_{-100}^{100}{f(x)}dx\]is equal to
A)
\[\int_{-100}^{100}{f({{x}^{2}})}\,dx\]
done
clear
B)
\[\int_{-100}^{100}{f(-{{x}^{2}})}\,dx\]
done
clear
C)
\[\int_{-100}^{100}{f\left( \frac{1}{x} \right)}\,dx\]
done
clear
D)
\[\int_{-100}^{100}{f(-x)}\,dx\]
done
clear
E)
\[\int_{-100}^{100}{[f(x)+f(-x)}]\,dx\]
done
clear
View Answer play_arrow
question_answer 173) \[\int_{-1}^{1}{({{e}^{{{x}^{3}}}}+{{e}^{-{{x}^{3}}}})({{e}^{x}}-{{e}^{-x}})}dx\]is equal to
A)
\[\frac{{{e}^{2}}}{2}-2e\]
done
clear
B)
\[{{e}^{2}}-2e\]
done
clear
C)
\[2({{e}^{2}}-e)\]
done
clear
D)
\[2{{e}^{2}}-2e\]
done
clear
E)
\[0\]
done
clear
View Answer play_arrow
question_answer 174) The family of curves\[y={{e}^{a\sin x}},\]where a is an arbitrary constant, is represented by the differential equation
A)
\[\log y=\tan x\frac{dy}{dx}\]
done
clear
B)
\[y\log y=\tan x\frac{dy}{dx}\]
done
clear
C)
\[y\log y=\sin x\frac{dy}{dx}\]
done
clear
D)
\[\log y=\cos x\frac{dy}{dx}\]
done
clear
E)
\[y\log y=\cos x\frac{dy}{dx}\]
done
clear
View Answer play_arrow
question_answer 175) The integrating factor of \[x\frac{dy}{dx}+(1+x)y=x\] is
A)
\[x\]
done
clear
B)
\[2x\]
done
clear
C)
\[{{e}^{x\log x}}\]
done
clear
D)
\[{{e}^{x}}\]
done
clear
E)
\[x{{e}^{x}}\]
done
clear
View Answer play_arrow
question_answer 176) The degree and order of the differential equation\[y=px+\sqrt[3]{{{a}^{2}}{{p}^{2}}+{{b}^{2}}},\]where\[p=\frac{dy}{dx},\]are respectively
A)
3, 1
done
clear
B)
1, 3
done
clear
C)
1, 1
done
clear
D)
3, 3
done
clear
E)
3, 2
done
clear
View Answer play_arrow
question_answer 177) The solution of the differential equation\[\frac{dy}{dx}+1={{e}^{x+y}}\]is
A)
\[x+{{e}^{x+y}}=c\]
done
clear
B)
\[x-{{e}^{x+y}}=c\]
done
clear
C)
\[x+{{e}^{-(x+y)}}=c\]
done
clear
D)
\[x-{{e}^{-(x+y)}}=c\]
done
clear
E)
\[x{{e}^{x+y}}+y=c\]
done
clear
View Answer play_arrow
question_answer 178) Let\[f(x)=\frac{a{{x}^{2}}}{x+1},x\ne -1,\]The value of a for which\[f(a)=a,(a\ne 0)\]is
A)
\[1-\frac{1}{a}\]
done
clear
B)
\[\frac{1}{a}\]
done
clear
C)
\[1+\frac{1}{a}\]
done
clear
D)
\[\frac{1}{a}-1\]
done
clear
E)
\[-\frac{1}{a}\]
done
clear
View Answer play_arrow
question_answer 179) For\[a,b\in R,\]define\[a*b=\frac{a}{a+b},\]where. \[a+b\ne 0.\]If\[a*b=5,\]then the value of\[b*a\]is
A)
5
done
clear
B)
\[-5\]
done
clear
C)
4
done
clear
D)
\[-7\]
done
clear
E)
\[-4\]
done
clear
View Answer play_arrow
question_answer 180) Let\[A=\{x,\text{ }y,\text{ }z\}\]and\[B=\{a,\text{ }b,\text{ }c,\text{ }d\}\]. Which one of the following is not a relation from A to B?
A)
\[\{(x,a),(x,c)\}\]
done
clear
B)
\[\{(y,c),(y,d)\}\]
done
clear
C)
\[\{(z,a),(z,d)\}\]
done
clear
D)
\[\{(z,b),(y,b),(a,b)\}\]
done
clear
E)
\[\{(x,c)\}\]
done
clear
View Answer play_arrow
question_answer 181) The domain of\[{{\sin }^{-1}}\left[ {{\log }_{2}}\left( \frac{x}{12} \right) \right]\]is
A)
\[[2,12]\]
done
clear
B)
\[[-1,1]\]
done
clear
C)
\[\left[ \frac{1}{3},24 \right]\]
done
clear
D)
\[\left[ \frac{2}{3},24 \right]\]
done
clear
E)
\[[6,24]\]
done
clear
View Answer play_arrow
question_answer 182) If\[f(x)={{x}^{2}}-1\]and\[g(x)={{(x+1)}^{2}},\]then\[(gof)(x)\]is
A)
\[{{(x+1)}^{4}}-1\]
done
clear
B)
\[{{x}^{4}}-1\]
done
clear
C)
\[{{x}^{4}}\]
done
clear
D)
\[{{(x+1)}^{4}}\]
done
clear
E)
\[{{(x-1)}^{4}}-1\]
done
clear
View Answer play_arrow
question_answer 183)
The shaded region in the figure represents
A)
\[A\cap B\]
done
clear
B)
\[A\cup B\]
done
clear
C)
\[B-A\]
done
clear
D)
\[A-B\]
done
clear
E)
\[(A-B)\cup (B-A)\]
done
clear
View Answer play_arrow
question_answer 184) If\[{{(x+iy)}^{1/3}}=2+3i,\]then\[3x+2y\]is equal to
A)
\[-20\]
done
clear
B)
\[-60\]
done
clear
C)
\[-120\]
done
clear
D)
60
done
clear
E)
\[156\]
done
clear
View Answer play_arrow
question_answer 185) The modulus of the complex number\[z\]such that\[|z+3-i|=1\]and \[arg\,(z)=\pi \] is equal to
A)
1
done
clear
B)
2
done
clear
C)
9
done
clear
D)
4
done
clear
E)
3
done
clear
View Answer play_arrow
question_answer 186) If\[{{z}_{1}},{{z}_{2}},......,{{z}_{n}}\]are complex numbers such that \[|{{z}_{1}}|=|{{z}_{2}}=.....=|{{z}_{n}}|=1,\]then \[|{{z}_{1}}+{{z}_{2}}+...+{{z}_{n}}|\]is equal to
A)
\[|{{z}_{1}}{{z}_{2}}{{z}_{3}}.....{{z}_{n}}|\]
done
clear
B)
\[|{{z}_{1}}|+|{{z}_{2}}|+....+|{{z}_{n}}|\]
done
clear
C)
\[\left| \frac{1}{{{z}_{1}}}+\frac{1}{{{z}_{2}}}+....+\frac{1}{{{z}_{n}}} \right|\]
done
clear
D)
\[n\]
done
clear
E)
\[\sqrt{n}\]
done
clear
View Answer play_arrow
question_answer 187) The value of\[\frac{\cos 30{}^\circ +i\sin 30{}^\circ }{\cos 60{}^\circ -i\sin 60{}^\circ }\]is equal to
A)
\[i\]
done
clear
B)
\[-i\]
done
clear
C)
\[\frac{1+\sqrt{3}i}{2}\]
done
clear
D)
\[\frac{1-\sqrt{3}i}{2}\]
done
clear
E)
\[1+i\]
done
clear
View Answer play_arrow
question_answer 188) If\[z=r(\cos \theta +i\sin \theta ),\]then the value of\[\frac{z}{z}=\frac{\overline{z}}{z}\]
A)
\[\cos 2\theta \]
done
clear
B)
\[2\cos 2\theta \]
done
clear
C)
\[2\cos \theta \]
done
clear
D)
\[2\sin \theta \]
done
clear
E)
\[2\sin 2\theta \]
done
clear
View Answer play_arrow
question_answer 189) If\[{{z}_{1}}=\sqrt{2}\left( \cos \frac{\pi }{4}+i\sin \frac{\pi }{4} \right)\]and\[{{z}_{2}}=\sqrt{3}\left( \cos \frac{\pi }{3}+i\sin \frac{\pi }{3} \right),\]then\[|{{z}_{1}}{{z}_{2}}|\]is
A)
\[6\]
done
clear
B)
\[\sqrt{2}\]
done
clear
C)
\[\sqrt{6}\]
done
clear
D)
\[\sqrt{3}\]
done
clear
E)
\[\sqrt{2}+\sqrt{3}\]
done
clear
View Answer play_arrow
question_answer 190) The value of a for which the equation\[2{{x}^{2}}+2\sqrt{6}x+a=0\]has equal roots, is
A)
3
done
clear
B)
\[4\]
done
clear
C)
2
done
clear
D)
\[\sqrt{3}\]
done
clear
E)
\[\sqrt{2}\]
done
clear
View Answer play_arrow
question_answer 191) If\[\frac{3}{2}+\frac{7}{2}i\]is a solution of the equation\[a{{x}^{2}}-6x+b=0,\]where a and b are real numbers, then the value of\[a+b\]is equal to
A)
10
done
clear
B)
22
done
clear
C)
30
done
clear
D)
29
done
clear
E)
31
done
clear
View Answer play_arrow
question_answer 192) If the roots of the equation\[{{x}^{2}}-bx+c=0\]are two consecutive integers, then\[{{b}^{2}}-4c\]is
A)
\[-1\]
done
clear
B)
0
done
clear
C)
1
done
clear
D)
2
done
clear
E)
3
done
clear
View Answer play_arrow
question_answer 193) If\[\alpha \]and\[\beta \]are the roots of the equation\[a{{x}^{2}}+bx+c=0,\]\[(c\ne 0),\]then the equation whose roots are\[\frac{1}{a\alpha +b}\]and\[\frac{1}{a\beta +b}\]is
A)
\[ac{{x}^{2}}-bx+1=0\]
done
clear
B)
\[{{x}^{2}}-acx+bc+1=0\]
done
clear
C)
\[ac{{x}^{2}}+bx-1=0\]
done
clear
D)
\[{{x}^{2}}+acx-bc+11=0\]
done
clear
E)
\[ac{{x}^{2}}-bx-11=0\]
done
clear
View Answer play_arrow
question_answer 194) If a and b are the roots of the equation \[{{x}^{2}}+ax+b=0,\]\[a\ne 0,b\ne 0,\]then the values of a and b are respectively
A)
2 and\[-2\]
done
clear
B)
2 and \[-1\]
done
clear
C)
1 and\[-2\]
done
clear
D)
1 and 2
done
clear
E)
\[-1\]and 2
done
clear
View Answer play_arrow
question_answer 195) If\[{{x}^{2}}+px+q=0\]has the roots\[\alpha \]and\[\beta \]then the value of\[{{(\alpha -\beta )}^{2}}\]is equal to
A)
\[{{p}^{2}}-4q\]
done
clear
B)
\[{{({{p}^{2}}-4q)}^{2}}\]
done
clear
C)
\[{{p}^{2}}+4q\]
done
clear
D)
\[{{({{p}^{2}}+4q)}^{2}}\]
done
clear
E)
\[{{q}^{2}}-4q\]
done
clear
View Answer play_arrow
question_answer 196) If the sum to first n terms of the AP 2, 4,6,... is 240, then the value of n is
A)
14
done
clear
B)
15
done
clear
C)
16
done
clear
D)
17
done
clear
E)
18
done
clear
View Answer play_arrow
question_answer 197) The value of \[\frac{1}{\sqrt{10}-\sqrt{9}}-\frac{1}{\sqrt{11}-\sqrt{10}}+\frac{1}{\sqrt{12}-\sqrt{11}}\]\[-....-\frac{1}{\sqrt{121}-\sqrt{120}}\] is equal to
A)
\[-10\]
done
clear
B)
11
done
clear
C)
14
done
clear
D)
13
done
clear
E)
\[-8\]
done
clear
View Answer play_arrow
question_answer 198) An AP consists of 23 terms. If the sum of the three terms in the middle is 141 and the sum of the last three terms is 261, then the first term is
A)
6
done
clear
B)
5
done
clear
C)
4
done
clear
D)
3
done
clear
E)
2
done
clear
View Answer play_arrow
question_answer 199) If\[{{a}_{1}},{{a}_{2}},{{a}_{3}},.....{{a}_{n}}\]On are in AP with common difference 5 and if\[{{a}_{i}}{{a}_{j}}\ne -1\]for, \[j=1,2,...,n,\]then \[{{\tan }^{-1}}\left( \frac{5}{1+{{a}_{1}}{{a}_{2}}} \right)+{{\tan }^{-1}}\left( \frac{5}{1+{{a}_{2}}{{a}_{3}}} \right)\]\[+....+{{\tan }^{-1}}\left( \frac{5}{1+{{a}_{n-1}}{{a}_{n}}} \right)\] Is equal to
A)
\[{{\tan }^{-1}}\left( \frac{5}{1+{{a}_{n}}{{a}_{n-1}}} \right)\]
done
clear
B)
\[{{\tan }^{-1}}\left( \frac{5{{a}_{1}}}{1+{{a}_{n}}{{a}_{1}}} \right)\]
done
clear
C)
\[{{\tan }^{-1}}\left( \frac{5n-5}{1+{{a}_{n}}{{a}_{1}}} \right)\]
done
clear
D)
\[{{\tan }^{-1}}\left( \frac{5n-5}{1+{{a}_{n}}{{a}_{n+1}}} \right)\]
done
clear
E)
\[{{\tan }^{-1}}\left( \frac{5n}{1+{{a}_{1}}{{a}_{n}}} \right)\]
done
clear
View Answer play_arrow
question_answer 200) The sum of all two digit natural numbers which leave a remainder 5 when they are divided by 7 is equal to
A)
715
done
clear
B)
702
done
clear
C)
615
done
clear
D)
602
done
clear
E)
589
done
clear
View Answer play_arrow
question_answer 201) Let a be a positive number such that the arithmetic mean of a and 2 exceeds their geometric mean by 1. Then, the value of a is
A)
3
done
clear
B)
5
done
clear
C)
9
done
clear
D)
8
done
clear
E)
10
done
clear
View Answer play_arrow
question_answer 202) The coefficient of the middle term in the expansion of\[{{(x+2y)}^{6}}\]is
A)
\[^{6}{{C}_{3}}\]
done
clear
B)
\[8{{(}^{6}}{{C}_{3}})\]
done
clear
C)
\[8{{(}^{6}}{{C}_{4}})\]
done
clear
D)
\[^{6}{{C}_{4}}\]
done
clear
E)
\[8{{(}^{6}}{{C}_{5}})\]
done
clear
View Answer play_arrow
question_answer 203) Let\[{{(1+x)}^{n}}=1+{{a}_{1}}x+{{a}_{2}}{{x}^{2}}+.....+{{a}_{n}}{{x}^{n}}\].If\[{{a}_{1}},{{a}_{2}}\]and\[{{a}_{3}}\]are in AP, then the value of n is
A)
4
done
clear
B)
5
done
clear
C)
6
done
clear
D)
7
done
clear
E)
8
done
clear
View Answer play_arrow
question_answer 204) The number of positive integers less than 40000 that can be formed by using all the digits 1, 2, 3, 4 and 5 is equal to
A)
24
done
clear
B)
78
done
clear
C)
32
done
clear
D)
216
done
clear
E)
72
done
clear
View Answer play_arrow
question_answer 205) If the sum of the coefficients in the expansion of\[{{({{a}^{2}}{{x}^{2}}-6ax+11)}^{10}},\]where a is constant, is 1024, then the value of a is
A)
5
done
clear
B)
1
done
clear
C)
2
done
clear
D)
3
done
clear
E)
4
done
clear
View Answer play_arrow
question_answer 206) If\[^{56}{{P}_{r+6}}{{:}^{54}}{{p}_{r+3}}=30800:1,\]then the value of r is
A)
40
done
clear
B)
51
done
clear
C)
101
done
clear
D)
410
done
clear
E)
41
done
clear
View Answer play_arrow
question_answer 207) From 12 books, the difference between number of ways a selection of 5 books when one specified book is always excluded and one specified book is always included is
A)
64
done
clear
B)
118
done
clear
C)
132
done
clear
D)
330
done
clear
E)
462
done
clear
View Answer play_arrow
question_answer 208) If\[A=\left[ \begin{matrix} x & -2 \\ 3 & 7 \\ \end{matrix} \right]\]and\[{{A}^{-1}}=\left[ \begin{matrix} \frac{7}{34} & \frac{1}{17} \\ \frac{-3}{34} & \frac{2}{17} \\ \end{matrix} \right]\],then the value of x is
A)
2
done
clear
B)
3
done
clear
C)
\[-4\]
done
clear
D)
4
done
clear
E)
\[-2\]
done
clear
View Answer play_arrow
question_answer 209) If\[\left| \begin{matrix} {{x}^{2}}+x & 3x-1 & -x+3 \\ 2x+1 & 2+{{x}^{2}} & {{x}^{3}}-3 \\ x-3 & {{x}^{2}}+4 & 3x \\ \end{matrix} \right|\] \[={{a}_{0}}+{{a}_{1}}x+{{a}_{2}}{{x}^{2}}+.....+{{a}_{7}}{{x}^{7}},\] then the value of\[{{a}_{0}}\]is
A)
25
done
clear
B)
24
done
clear
C)
23
done
clear
D)
22
done
clear
E)
21
done
clear
View Answer play_arrow
question_answer 210) The value of the determinant\[\left| \begin{matrix} 15! & 16! & 17! \\ 16! & 17! & 18! \\ 17! & 18! & 19! \\ \end{matrix} \right|\]is equal to
A)
\[15!+16!\]
done
clear
B)
\[2(15!)(16!)(17!)\]
done
clear
C)
\[15!+16!+17!\]
done
clear
D)
\[16!+17!\]
done
clear
E)
\[2(15!+16!)\]
done
clear
View Answer play_arrow
question_answer 211) If A is a non-singular matrix of order 3, then adj (adj A) is equal to
A)
\[A\]
done
clear
B)
\[{{A}^{-1}}\]
done
clear
C)
\[\frac{1}{|A|}A\]
done
clear
D)
\[|A|A\]
done
clear
E)
\[\frac{1}{|A|}{{A}^{-1}}\]
done
clear
View Answer play_arrow
question_answer 212) If \[\left[ \begin{matrix} x-y-x \\ -y+z \\ z \\ \end{matrix} \right]=\left[ \begin{matrix} 0 \\ 5 \\ 3 \\ \end{matrix} \right],\]then the values of\[x,y\] and\[z\]are respectively
A)
\[5,2,2\]
done
clear
B)
\[1,-2,3\]
done
clear
C)
\[0,-3,3\]
done
clear
D)
\[11,8,3\]
done
clear
E)
\[4,1,3\]
done
clear
View Answer play_arrow
question_answer 213) Which one of the following is true always for any two non-singular matrices A and B of same order?
A)
\[AB=BA\]
done
clear
B)
\[{{(AB)}^{t}}={{A}^{t}}{{B}^{t}}\]
done
clear
C)
\[(A+B)(A-B)={{A}^{2}}-{{B}^{2}}\]
done
clear
D)
\[{{(AB)}^{-1}}={{B}^{-1}}{{A}^{-1}}\]
done
clear
E)
\[AB=-BA\]
done
clear
View Answer play_arrow
question_answer 214) The solution set of the in equation\[\frac{x+11}{x-3}>0\]is
A)
\[(-\infty ,-11)\cup (3,\infty )\]
done
clear
B)
\[(-\infty ,-10)\cup (2,\infty )\]
done
clear
C)
\[(-100,-11)\cup (1,\infty )\]
done
clear
D)
\[(0,5)\cup (-1,0)\]
done
clear
E)
\[(-5,0)\cup (3,7)\]
done
clear
View Answer play_arrow
question_answer 215) If\[3\le 3t-18\le 18,\]then which one of the following is true?
A)
\[15\le 2t+1\le 20\]
done
clear
B)
\[8\le t<12\]
done
clear
C)
\[8\le t+1\le 13\]
done
clear
D)
\[21\le 3t\le 24\]
done
clear
E)
\[t\le 7\]or\[t\ge 12\]
done
clear
View Answer play_arrow
question_answer 216) Let p: 7 is not greater than 4 and q: Paris is in France be two statements. Then,\[\tilde{\ }(p\vee q)\]is the statement
A)
7 is greater than 4 or Paris is not in France
done
clear
B)
7 is not greater than 4 and Paris is not in France
done
clear
C)
7 is greater than 4 and Paris is in France
done
clear
D)
7 is not greater than 4 or Paris is not in France
done
clear
E)
7 is greater than 4 and Paris is not in France
done
clear
View Answer play_arrow
question_answer 217) If\[S(p,q,r)=(\tilde{\ }p)\vee [\tilde{\ }(q\vee r)]\]is a compound statement, then\[S(\tilde{\ }p,\tilde{\ }q,\tilde{\ }r)\]is
A)
\[-S(p,q,r)\]
done
clear
B)
\[S(p,q,r)\]
done
clear
C)
\[p\vee (q\wedge r)\]
done
clear
D)
\[p\vee (q\vee r)\]
done
clear
E)
\[S(p,q,\tilde{\ }r)\]
done
clear
View Answer play_arrow
question_answer 218) For any two statements p and\[q,\tilde{\ }(p\vee q)\vee (\tilde{\ }p\wedge q)\]is logically equivalent to
A)
p
done
clear
B)
\[\tilde{\ }p\]
done
clear
C)
q
done
clear
D)
\[\tilde{\ }q\]
done
clear
E)
\[p\vee q\]
done
clear
View Answer play_arrow
question_answer 219) If\[\tan \alpha =\frac{b}{a},a>b>0\]and if\[0<\alpha <\frac{\pi }{4},\]then\[\sqrt{\frac{a+b}{a-b}}-\sqrt{\frac{a-b}{a+b}}\]is equal to
A)
\[\frac{2\sin \alpha }{\sqrt{\cos 2\alpha }}\]
done
clear
B)
\[\frac{2\cos \alpha }{\sqrt{\cos 2\alpha }}\]
done
clear
C)
\[\frac{2\sin \alpha }{\sqrt{\sin 2\alpha }}\]
done
clear
D)
\[\frac{2\cos \alpha }{\sqrt{\sin 2\alpha }}\]
done
clear
E)
\[\frac{2\tan \alpha }{\sqrt{\cos 2\alpha }}\]
done
clear
View Answer play_arrow
question_answer 220) If\[{{\tan }^{-1}}(x+2)+{{\tan }^{-1}}(x-2)-{{\tan }^{-1}}\left( \frac{1}{2} \right)=0,\]then one of the values of\[x\]is equal to
A)
\[-1\]
done
clear
B)
\[5\]
done
clear
C)
\[\frac{1}{2}\]
done
clear
D)
\[1\]
done
clear
E)
\[-\frac{1}{2}\]
done
clear
View Answer play_arrow
question_answer 221) If\[\alpha ,\beta \in \left( 0,\frac{\pi }{2} \right),\sin \alpha =\frac{4}{5}\]\[\cos (\alpha +\beta )=-\frac{12}{13},\]then\[\sin \beta \]is equal to
A)
\[\frac{63}{65}\]
done
clear
B)
\[\frac{61}{65}\]
done
clear
C)
\[\frac{3}{5}\]
done
clear
D)
\[\frac{5}{13}\]
done
clear
E)
\[\frac{8}{65}\]
done
clear
View Answer play_arrow
question_answer 222) The number of solutions of\[\cos 2\theta =\sin \theta \]in\[(0,2\pi )\]is
A)
1
done
clear
B)
2
done
clear
C)
3
done
clear
D)
4
done
clear
E)
0
done
clear
View Answer play_arrow
question_answer 223) The value of\[{{\sin }^{-1}}\left( \frac{4}{5} \right)+2{{\tan }^{-1}}\left( \frac{1}{3} \right)\]is equal to
A)
\[\frac{\pi }{3}\]
done
clear
B)
\[\frac{\pi }{4}\]
done
clear
C)
\[\frac{\pi }{2}\]
done
clear
D)
\[\pi \]
done
clear
E)
\[2\pi \]
done
clear
View Answer play_arrow
question_answer 224) The value of \[tan\text{ }40{}^\circ +tan\text{ }20{}^\circ +\sqrt{3}\text{ }tan\text{ }20{}^\circ tan\text{ }40{}^\circ \]is equal to
A)
\[\sqrt{12}\]
done
clear
B)
\[\frac{1}{\sqrt{3}}\]
done
clear
C)
1
done
clear
D)
\[\frac{\sqrt{3}}{2}\]
done
clear
E)
\[\sqrt{3}\]
done
clear
View Answer play_arrow
question_answer 225) The period of the function\[f(\theta )=4+4{{\sin }^{3}}\theta -3\sin \theta \]is
A)
\[\frac{2\pi }{3}\]
done
clear
B)
\[\frac{\pi }{3}\]
done
clear
C)
\[\frac{\pi }{2}\]
done
clear
D)
\[\pi \]
done
clear
E)
\[2\pi \]
done
clear
View Answer play_arrow
question_answer 226) The value of\[x\]in\[\left( 0,\frac{\pi }{2} \right)\]satisfying the equation \[\sin x\cos x=\frac{1}{4}\]is
A)
\[\frac{\pi }{6}\]
done
clear
B)
\[\frac{\pi }{3}\]
done
clear
C)
\[\frac{\pi }{8}\]
done
clear
D)
\[\frac{\pi }{4}\]
done
clear
E)
\[\frac{\pi }{12}\]
done
clear
View Answer play_arrow
question_answer 227) The value of\[{{\sin }^{-1}}\{\cos (4095{}^\circ )\}\]is equal to
A)
\[-\frac{\pi }{3}\]
done
clear
B)
\[\frac{\pi }{6}\]
done
clear
C)
\[-\frac{\pi }{4}\]
done
clear
D)
\[\frac{\pi }{4}\]
done
clear
E)
\[\frac{\pi }{2}\]
done
clear
View Answer play_arrow
question_answer 228) If the distance between (2, 3) and\[(-\text{ }5,\text{ }2)\] is equal to the distance between\[(x,\text{ }2)\]and (1,3), then the values of \[x\]are
A)
\[-6,8\]
done
clear
B)
\[6,8\]
done
clear
C)
\[-8,6\]
done
clear
D)
\[-7,7\]
done
clear
E)
\[-8,-6\]
done
clear
View Answer play_arrow
question_answer 229) The line segment joining the points (4, 7) and \[(-2,-1)\]is a diameter of a circle. If the circle intersects the x-axis at A and B, then AB is equal to
A)
4
done
clear
B)
5
done
clear
C)
6
done
clear
D)
7
done
clear
E)
8
done
clear
View Answer play_arrow
question_answer 230) If the three points (0, 1),\[(0,-1)\]and\[(x,0)\]are vertices of an equilateral triangle, then the values of\[x\]are
A)
\[\sqrt{3},\sqrt{2}\]
done
clear
B)
\[\sqrt{3},-\sqrt{3}\]
done
clear
C)
\[-\sqrt{5},\sqrt{3}\]
done
clear
D)
\[\sqrt{2},-\sqrt{2}\]
done
clear
E)
\[\sqrt{5},-\sqrt{5}\]
done
clear
View Answer play_arrow
question_answer 231) The area of the triangle formed by the points (2, 2), (5, 5), (6, 7) is equal to (in square units)
A)
9
done
clear
B)
5
done
clear
C)
10
done
clear
D)
3
done
clear
E)
14
done
clear
View Answer play_arrow
question_answer 232) If the line\[px-qy=r\]intersects the coordinate axes at (a, 0) and (0, b), then the value of\[a+b\]is equal to
A)
\[r\left( \frac{q+p}{pq} \right)\]
done
clear
B)
\[r\left( \frac{q-p}{pq} \right)\]
done
clear
C)
\[r\frac{(p-q)}{pq}\]
done
clear
D)
\[r\left( \frac{p+q}{p-q} \right)\]
done
clear
E)
\[r\left( \frac{p-q}{p+q} \right)\]
done
clear
View Answer play_arrow
question_answer 233) The vertices of a triangle are A (3, 7), B (3, 4) and C (5, 4). The equation of the bisector of the angle ABC is
A)
\[y=x+1\]
done
clear
B)
\[y=x-1\]
done
clear
C)
\[y=3x-5\]
done
clear
D)
\[y=x\]
done
clear
E)
\[y=-x\]
done
clear
View Answer play_arrow
question_answer 234) The equation of a straight line which passes through the point\[(a{{\cos }^{3}}\theta ,a{{\sin }^{3}}\theta )\]and perpendicular to\[x\sec \theta +y\cos ec\theta =a\]is
A)
\[\frac{x}{a}+\frac{y}{a}=a\cos \theta \]
done
clear
B)
\[x\text{ }cos\theta -y\text{ }sin\theta =a\text{ }cos2\theta \]
done
clear
C)
\[x\text{ }cos\theta +y\text{ }sin\theta =a\text{ }cos\text{ }2\theta \]
done
clear
D)
\[x\text{ }cos\theta +y\text{ }sin\theta -a\text{ }cos\text{ }2\theta =1\]
done
clear
E)
\[x\text{ }cos\theta -y\text{ }sin\theta +a\text{ }cos\text{ }2\theta =-1\]
done
clear
View Answer play_arrow
question_answer 235) The slopes of the lines which make an angle \[45{}^\circ \]with the line\[3x-y=-5\]are
A)
\[1,-1\]
done
clear
B)
\[\frac{1}{2},-1\]
done
clear
C)
\[1,\frac{1}{2}\]
done
clear
D)
\[2,-\frac{1}{2}\]
done
clear
E)
\[-2,\frac{1}{2}\]
done
clear
View Answer play_arrow
question_answer 236) The equation of one of the lines parallel to \[4x-3y=5\]and at a unit distance from the point\[(-1,-4)\]is
A)
\[3x+4y-3=0\]
done
clear
B)
\[3x+4y+3=0\]
done
clear
C)
\[4x-3y+3=0\]
done
clear
D)
\[4x-3y-3=0\]
done
clear
E)
\[4x-3y-4=0\]
done
clear
View Answer play_arrow
question_answer 237) The equation of family of circles with centre at\[(h,\text{ }k)\]touching the\[x-\]axis is given by
A)
\[{{x}^{2}}+{{y}^{2}}-2hx+{{h}^{2}}=0\]
done
clear
B)
\[{{x}^{2}}+{{y}^{2}}-2hx-2fy+{{h}^{2}}=0\]
done
clear
C)
\[{{x}^{2}}+{{y}^{2}}-2hx-2ky-{{h}^{2}}=0\]
done
clear
D)
\[{{x}^{2}}-{{y}^{2}}-2hx-2ky=0\]
done
clear
E)
\[{{x}^{2}}+{{y}^{2}}+2hx+2ky=0\]
done
clear
View Answer play_arrow
question_answer 238) If the two circles\[{{(x+7)}^{2}}+{{(y-3)}^{2}}=36\]and \[{{(x-5)}^{2}}+{{(y+2)}^{2}}=49\]touch each other externally, then the point of contact is
A)
\[\left( \frac{-19}{13},\frac{19}{13} \right)\]
done
clear
B)
\[\left( \frac{-19}{13},\frac{9}{13} \right)\]
done
clear
C)
\[\left( \frac{17}{13},\frac{9}{13} \right)\]
done
clear
D)
\[\left( \frac{-17}{13},\frac{9}{13} \right)\]
done
clear
E)
\[\left( \frac{19}{13},\frac{19}{13} \right)\]
done
clear
View Answer play_arrow
question_answer 239) The equation of the chord of the circle \[{{x}^{2}}+{{y}^{2}}=81\] which is bisected at the point \[(-2,3)\]is
A)
\[3x-y=13\]
done
clear
B)
\[3x-4y=13\]
done
clear
C)
\[2x-3y=13\]
done
clear
D)
\[3x-3y=13\]
done
clear
E)
\[2x-3y=-13\]
done
clear
View Answer play_arrow
question_answer 240) The distance of the midpoint of line joining two points (4, 0) and (0, 4) from the centre of the circle\[{{x}^{2}}+{{y}^{2}}=16\]is
A)
\[\sqrt{2}\]
done
clear
B)
\[2\sqrt{2}\]
done
clear
C)
\[3\sqrt{2}\]
done
clear
D)
\[2\sqrt{3}\]
done
clear
E)
\[\sqrt{3}\]
done
clear
View Answer play_arrow
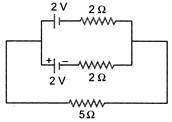
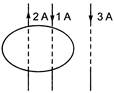
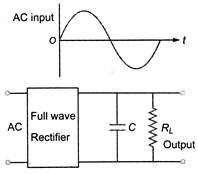 The output voltage across\[{{R}_{L}}\]is represented as
The output voltage across\[{{R}_{L}}\]is represented as